环境激励下二滩拱坝拍振机理的研究

练继建，李成业，刘 昉，宋明富

（1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072；2.二滩水力发电厂，四川 攀枝花 617000）

目前，我国水能资源开发的重点集中在西北的黄河上游、西南的金沙江、雅砻江、澜沧江、大渡河等干支流，上述河流大都具有“山高、谷陡、洪水峰高量大”的特点，同时这些地区居民少，移民工作简单，库区容易产生新的生态平衡，适于修建大型水利工程［1］。随着我国建坝技术的不断提高，以240 m级的二滩拱坝为起点，金沙江溪洛渡（坝高278 m）、黄河拉西瓦（坝高252 m）、乌江构皮滩（坝高231 m）、澜沧江小湾（坝高292 m）、雅砻江锦屏（坝高305 m）等超高坝相继开始建设。这些高拱坝大多修建在深山峡谷之中，且普遍采用表、中孔联合泄洪，水垫塘消能的布置型式，在汛期坝身需集中宣泄大量的洪水，由此产生各种动力荷载，将不同程度地诱发坝体振动，形成泄流激励下拱坝－地基－库（静）水耦合系统的随机振动问题。

由于条件限制，我国对拱坝泄洪振动的原型观测资料不多。天津大学结合二滩工程开发了“高坝泄流结构安全网络监测系统”，实现了对高坝泄流结构的实时在线监测，并于2009年汛期对二滩拱坝泄洪诱发振动情况进行了原型观测。观测结果表明，实测坝身最大振动响应均方根为24 μm，最大双倍振幅为183 μm，泄洪振动不会对拱坝本身的安全构成威胁。但是观察各工况下坝体振动响应的时程曲线，看到波的包络线随时间增大或减小的现象，在这段曲线中，波形很光滑，振幅比较大，波形非常像振动中“拍”的现象。表1给出了我国部分已建成和在建高拱坝的体型参数和基频类比［2］，各工程坝体的体型参数和基频具有一定的相似性，因此研究环境激励下二滩拱坝的拍振机理，对其他在建工程的施工和运行维护具有重要意义。

本文研究泄流激励下二滩拱坝的拍振机理，首先引入自然界中“拍”的概念，研究了初相差、频率比和振幅比对“拍”的影响，并分析了多列波合成拍的特性；然后应用自回归AR模型对坝体实测数据进行主频统计分析，同时应用SSI法求出坝体泄洪振动的前四阶振型；最后结合实测拍振现象的自身特点，对泄洪激励下二滩拱坝拍振现象的机理进行研究。

表1 我国部分已建和在建拱坝的体型参数和基频类比Tab.1 Analogy on shape parameter and fundamental frequency of some arch dams in china under-construction and in built

1 拍振波形的合成

“拍”是自然界中非常普遍的一种现象，当两个频率相差不大的同向简谐振动合成时，其合成波形的振幅将随时间作周期性的缓慢变化，这种现象就称为“拍”现象［3－5］。

将两个振幅、角频率和初相位都不相同的简谐振动进行叠加，设两个分振动的方程为：

式中：分振动1和分振动2的振幅分别为A1和A2，角频率分别为ω1和ω2，初相位分别为φ10和φ20。

合成振动的振幅为：

合成振动的角频率为：

式中，β=A1/A2为振幅比，当β=1时，合成振动的角频率ω=（ω1+ω2）/2。

（1）初相差φ20－φ10对合成“拍”的影响

初相差只是影响波形包络线的位置，对“拍”不产生实质性的影响，如图1所示。

图1 初相差改变对“拍”的影响Fig.1 Effect on“beat”caused by initial phase difference changing

（2）频率比ξ对合成“拍”的影响

设两分振动的振幅A1=A2=A，且两分振动的初始相位φ10=φ20=0，则合振动可写为：

当n=6时，合振动的波形才能明显地表现出“拍”现象，此时，频率比ξ满足0.85≤ξ≤1.18 且ξ≠1。

（3）振幅比β对合成“拍”的影响

振幅比β主要影响合振动的振幅，图2给出了振幅比β分别取0.2、1和4时合振动的波形曲线。当β在1附近时，“拍”现象明显，“拍”形较完整；而当β远离1时，合振幅的包络线比较平缓，“拍”现象不是十分明显。当0.33＜β＜3.0时，能够明显地观察到“拍”现象。从图中还可以看出，振幅比的变化对包络线的周期（“拍”的周期）不产生影响。

以上分析表明，当两列波的振幅比β和频率比ξ满足式（5）时，它们的合成波形就会出现明显的“拍”现象。

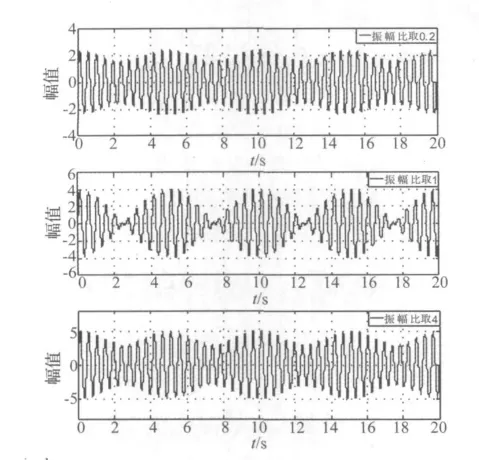
图2 β取不同值时对合振动振幅包络线的影响Fig.2 Influence on resultant vibration amplitude envelope caused by different β

实际工程采集到信号往往是由三个或三个以上分振动叠加合成的，分析可知，n个分量中任意两个分量的振幅比和频率比同时满足式（5）的条件，则n个分量叠加后会出现明显的“拍”现象。

2 坝体泄洪振动测点布置及测试工况

为了对二滩拱坝坝身的运行和健康状况进行有效监测，在坝顶2#～38#坝段，每隔5个坝段布置一个传感器，布置B1～B7共7个测点；在拱冠梁（20#坝段）自上而下依次布置B8（1 169 m高程）、B9（1 139 m高程）、B10（1 091 m高程）、B11（1 040 m高程）共4个测点，形成了11个测点、“T”型分布的监测网络。该测点网络覆盖了拱坝的坝顶拱圈和拱冠梁，传感器具体位置如图3所示。

图3 二滩坝体振动观测点布置图Fig.3 Arrangement plan of vibration observed points in Ertan dam body

2009年汛期期间，我们连续3天对坝体的泄洪振动进行了观测，并总结了较为重要的5种测试工况，见表2。

表2 二滩振动观测典型工况表Tab.2 Typical conditions of Ertan vibration observation

3 泄洪激励下二滩拱坝的振型识别

3.1 基于随机子空间方法的二滩拱坝振型识别

随机子空间识别法（SSI）［6－8］是近年来国内外研究的一个热点方法。与传统的频域识别方法相比，SSI法直接对时域数据进行分析，能准确识别系统的频率、模态阻尼和振型，使识别结果更有意义和实用价值。以实测坝顶7个测点的时程数据作为SSI法的输入，对二滩拱坝进行模态参数识别。

表3给出了SSI法和峰值法识别的结果对比，两种方法识别的频率相差很小，说明SSI法具有较高的识别精度。图4给出了SSI方法识别的二滩拱坝前四阶振型，其中一阶为正对称，二阶为反对称，三阶为正对称，四阶为正对称。

表3 SSI法识别结果与峰值法识别的结果对比Tab.3 Identification results comparison between SSI and peak value method

图4 SSI方法前四阶振型识别结果Fig.4 First four order vibration modes based on SSI

3.2 坝体测点主频统计

考虑到传统的基于FFT求得的功率谱曲线起伏比较剧烈，方差较大，在主频段处存在许多虚假的峰值，本文应用自回归AR模型计算实测数据的功率谱密度［9－10］，该方法求得的功率谱密度曲线比较平滑，方差较小，没有虚假峰值的存在，主频率明确。对坝体11个测点的主频率值按照坝顶拱圈和拱冠梁方向分别进行统计，其中B1和B7测点靠近坝肩，噪声污染严重，其主频值不予考虑，统计结果如表4和表5所示。

表4 典型工况下坝顶拱圈上各测点泄洪振动主频统计Tab.4 Dominant frequency statistical of different measuring point on dam crest arch ring in typical conditi on

从表4和表5的主频统计结果可以看出，拱圈上B2、B3、B5、B6 测点在各工况下主频均在 1.52 ～1.53 Hz之间，而各工况下拱冠梁上测点的主频值均在1.42～1.45 Hz之间。结合各测点功率谱图上体现的特征频率，位于拱冠梁上的测点一般只能识别出一阶频率或者一阶频率为主，位于拱圈上的B2、B3、B5、B6测点能够识别出二阶频率，表明泄洪激励下二滩拱坝的一阶振型为正对称，二阶为反对称，与SSI法识别出的拱坝前两阶振型结果相同。

表5 典型工况下拱冠梁上各测点泄洪振动主频统计Tab.5 Dominant frequency statistical of different measuring point on crown cantilever in typical condition

4 二滩拱坝泄洪振动的拍振机理研究

图5给出了坝顶拱圈B3和B5测点的振动位移时程图，从图中可以看出，B3和B5测点的位移时程曲线存在明显的“拍”现象。

图6（a）和图6（b）给出了B3和B5测点在工况1条件下的功率谱密度图，图中在f1=1.44 Hz和f2=1.53 Hz处均有明显峰值，说明B3和B5测点信号中同时含有拱坝的前两阶模态分量，且频率比f1/f2=0.94在式（5）的范围内，这就为“拍”的形成提供了条件。从功率谱图上还可以直观地看出，B3测点一、二阶工作频率对应的峰值基本相等，说明前两阶振型振动的能量基本相等；而B5测点，二阶工作频率对应的峰值远大于一阶，说明其二阶振型振动的能量远大于一阶，这种现象在各泄洪工况中均有体现。

从B3和B5测点的时程图中可以看出，拍振现象不是在任何时刻都有发生，拍的出现具有一定的随机性，其形状也不是一成不变的，而是随着采集时间不断发生变化。

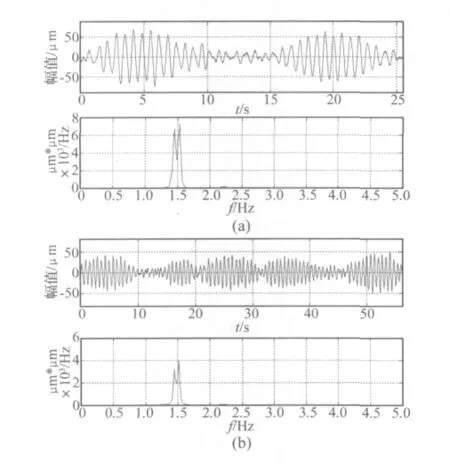
图7 （a）工况1B3测点145.5～171 s内波形图及其功率谱密度曲线；（b）工况1B3测点177～233.25 s内波形图及其功率谱密度曲线Fig.7（a）Oscillogram and power spectral density curve of point B3 for condition One during 145.5seconds to 171 seconds；（b）oscillogram and power spectral density curve of point B3 for condition One during 177seconds to 233.25seconds.

图7（a）和图7（b）分别给出了B3测点位移时程线中不同时间内的两段波形及各自的功率谱密度曲线。其中（a）图中两个拍的振幅和周期基本相同，由振幅比β对合成“拍”形的影响可知，两个分振动的振幅比近似为1，在功率谱图中体现为频率f1=1.445 Hz、f2=1.529 Hz处对应的峰值近似相等；图7（b）图波形中共含有5个拍，其功率谱密度曲线在1.44 Hz和1.53 Hz存在两个近似相等的峰值。由坝体测点频率统计分析以及SSI法模态识别结果可知，泄洪激励下二滩拱坝的一阶工作频率为1.42～1.45 Hz，振型为正对称，二阶工作频率为1.52～1.53 Hz，振型为反对称。由于相近的前两阶工作频率，并且前两阶振型在B3测点处均比较明显，B3测点的拍振现象主要是由前两阶振型叠加而成。

从各工况的功率谱图上可以看出，B5测点前两阶振型振动的能量相差很大，在幅值域上则表现为二阶振型为主的振动幅值较一阶振型大，使得前两阶振型在B5和B3测点处合成的拍存在明显的差异，主要体现在B5测点处拍的包络线变化缓慢，不同的拍形之间没有清晰的界限。

图8 工况1B5测点141.825 s～173.7 s内波形图及其功率谱密度曲线Fig.8 Oscillogram and power spectral density curve of point B5 for condition One during 141.825 seconds to 173.7 seconds.

图8给出了B5测点位移时程线中的一段波形及其功率谱密度曲线，图中含有4个拍形，每个拍的包络线变化缓慢，不同的拍形之间的界限模糊，各个拍的振幅和周期均存在一定的差异。根据多列波合成拍的特性以及不同振幅比对合成拍形的影响可以判定，图8的波形是由三个或三个以上的分量合成的，且各个分量间的振幅比均不等于1。应用现代谱分析方法求得其功率谱密度曲线，曲线共含有 1.53 Hz、1.42 Hz、1.32 Hz三个峰值，说明这段波形是由这三个频率成分为主的分量相互叠加而成的。

由上面的分析可知，B5测点处拍振现象的成因较B3测点复杂，对时程曲线按拍形的分布逐段进行分析，各个拍主要是由 1.53 Hz、1.42 Hz 和频带 1.27 Hz～1.39 Hz所对应的三个振动分量相互叠加而成。

拱冠梁上各测点时程曲线也存在明显的拍振现象，如图9所示。

图10给出了B9测点在工况1条件下的功率谱密度曲线，曲线在 1.44 Hz、1.52 Hz、1.39 Hz 和 1.33 Hz处存在峰值，其中一阶工作频率1.44 Hz对应的功率谱密度值最大。由频谱分析和SSI法模态识别结果可知，拱冠梁上各测点以一阶振型振动为主，且各测点位于拱坝二阶振型的节点附近，二阶振型振动对梁上测点的影响较小。此外，拱冠梁上测点也存在频率为1.27～1.39 Hz的振动分量，拍振现象的特点和成因与B5测点类似，如图11所示。

图11 工况1拱冠梁上B9测点139.3～189 s内的一段“拍”形Fig.11 A beat movement of point B9 for condition One during 139.3 seconds to 189 seconds

由模态识别的结果可知，频率为1.44 Hz和1.53 Hz的分量分别对应拱坝的前两阶振型振动，根据二滩拱坝的自身性质和工作条件，频带f=1.27～1.39 Hz所对应的振动分量可能由下面三种原因产生：

（1）拱坝自身的振型振动

由于f=1.27～1.39 Hz对应的分量振动量级较小，要想识别出这一振动分量，对方法的分辨率要求较高，文献［11］应用EMD分解取得了较好的效果。对各工况坝顶拱圈测点的振动响应信号进行EMD分解，多数测点信号中含有频率为1.25～1.39 Hz的 IMF分量，应用RDT+STD法对这些IMF分量的模态参数进行识别，识别的频率和阻尼比如表6所示。通常认为阻尼比小于1%或大于10%的识别结果均为虚假模态，表6中的识别频率在1.18～1.39 Hz范围内，阻尼比在10.63% ～58.6%范围内，可以认为是结构的虚假模态，所以频带f所对应的振动分量不是结构自身的振型振动。

表6 RDT+STD法识别特定IMF分量的频率和阻尼比Tab.6 Frequency and damp ratio of special IMFs used by RDT+STD

（2）水流脉动荷载作用于拱坝产生的受迫振动

高拱坝泄洪水流脉动荷载复杂多样，包括：① 挑跌流水舌冲击水垫塘底板的脉动荷载；② 直接作用于拱坝坝体下游面的“波浪”脉动荷载；③ 泄流孔口上的脉动荷载。水流脉动荷载频带主要集中在1～2 Hz之间，在泄洪工况下，水流脉动荷载可能使拱坝产生频带为f=1.27～1.39 Hz的受迫振动，与前两阶振型振动合成拍振现象。但是，对静水工况采集的数据进行EMD分析，在坝体不泄洪的条件下，f所对应的振动分量依然存在，如图12所示。说明泄洪条件下水流脉动荷载只是拱坝产生振动的一个激励源，它使拱坝产生的受迫振动不是产生拍振的主要分量。

图12 工况3B5测点EMD分解后第7阶分量及其功率谱密度曲线Fig.12 The seventh step of point B5 for condition three used by EMD and its power spectral density curve

（3）各坝段间横缝由于接触非线性引起的振动

混凝土拱坝施工时，为了便于浇筑混凝土和温度控制，不得不将拱坝分成若干个坝段，各坝段间沿拱向设有均匀排列的伸缩横缝。这些缝的存在极大地改善了坝体受力状况，但是也在一定程度上破坏了拱坝的整体性，使得在分析外部激励或者环境激励下坝体的动力特性时产生接触非线性的问题。对拱坝接触非线性问题的研究主要停留在接缝模型的数值模拟和模型试验两方面，缺乏原型观测数据的验证。文献［12］介绍了Kuo等提出的界面涂抹裂缝模型，该方法假设接缝处无滑动，接缝面上的摩擦力足以阻止界面滑动，这种假设与拱坝泄洪激励下各坝段间振动特性相似，应用此模型对二维拱肋进行计算，结果表明：由于收缩缝的非线性作用，增大了结构的位移及周期；同时在动力荷载作用下，接缝两块之间的惯性作用明显降低了接缝面上的受压荷载。基于以上分析，在泄洪激励或者大地脉动条件下，坝体各坝段间由于接触非线性而产生振动，振动频率随着激励荷载频率的变化而变化，当振动的频率与拱坝前两阶工作频率接近时，将产生拍振现象。当然，由坝段间接触非线性引起的振动只是一种假设，这种振动形式的存在性需要通过理论分析、模型计算和进一步的原型观测来验证。

5 结论

泄流诱发结构振动是一种极其复杂的流体与结构相互作用的现象。在水利工程中，随着高水头、大流量、超高流速泄水建筑物的兴建，以及工程结构趋于轻型化，水流诱发振动问题更加突出。本文针对实测二滩拱坝泄洪振动过程中出现的拍振现象，进行一系列分析，得到以下主要结论：

（1）通过分析，两个分振动的初相差对“拍”的图形不产生实质的影响，只是影响波形包络线的位置；频率比是形成“拍”的必要条件，只有当频率比ξ满足0.85≤ξ≤1.18且 ξ≠1时，才有可能出现“拍”现象；振幅比对“拍”的频率和振幅都会产生较大的影响，在频率比满足要求的前提下，只有当振幅比β满足0.33＜β＜3.0时，才能够明显地观察到“拍”现象。此外，多列波彼此之间的振幅比和频率比都满足要求时，也会形成“拍”现象，此时的波形常具有大尺度“拍”与小尺度“拍”交替出现的现象。

（2）应用随机子空间（SSI）方法和频谱分析方法，对二滩拱坝的模态参数进行识别，结果表明，泄洪激励下二滩拱坝的前两阶工作频率分别为1.44 Hz和1.53 Hz，一阶振型为对称振型，二阶为反对称振型。

（3）拱圈上B3测点的拍形完整、每个拍的周期和振幅相差不大，其拍振现象主要是由拱坝前两阶振型叠加而成的；拱圈上B5测点与拱冠梁上测点的拍形包络线变化缓慢，不同的拍形之间的界限模糊，各个拍的振幅和周期存在一定的差异，其时程曲线具有多列波叠加合成“拍”的特点，分析表明诱发这些测点拍振的原因除了结构自身的前两阶振型振动外，还有一个频带在1.27～1.39Hz的振动分量参与了拍的合成。通过分析，认为坝段间横缝的接触非线性是引起的这一振动的主要原因。但这只是一种假设，这种振动形式的存在性还需要通过理论分析、模型计算和进一步的原型观测来验证。

［1］潘家铮，何 璄.中国大坝五十年［M］.北京：中国水利水电出版社，2002.

［2］练继建，杨 敏，李火坤，等.高坝泄流工程［M］.北京：中国水利水电出版社，2008.

［3］应怀樵.波形和频谱分析与随机数据处理［M］.北京：中国铁道出版社，2003.

［4］苏未安，陈秀洪.用旋转矢量法研究“拍”现象［J］.江西理工大学学报，2009，30（1）：60 －63.

［5］周康魂.拍现象与外差变频的区别［J］.大学物理，1983，5：1－4.

［6］Peeter B，De Roeck G.Stochastic subspace techniques applied to parameteridentification ofcivilengineering structures［A］.Proceeding of New Advances in Modal YunthesisofLarge Structures：Nonlinear，Damped and Nondeterministic Cases，Lyon，France，September，1995，151－162.

［7］ Peeters B，De Roeck G.Reference-based stochastic subspace identification for output-only modal analysis［J］.Mechanical System and Signal Processing，1999，13（6）：855 －878.

［8］ Chen A l，Zhang L M.Study of stochastic subspace system identification method［J］.Chinese Journal of Aeronautics，2001，14（4）：222 －228.

［9］刘 昉，练继建，辜晋德.基于自回归模型的水流脉动压力频谱特征研究［J］.水力学报，2009，40（11）：1397－1402.

［10］胡广书.数字信号处理［M］.北京：清华大学出版社，2003.

［11］李成业.基于HHT的二滩拱坝工作性态识别及其“拍振”机理研究［D］.天津：天津大学，2010.

［12］晏启祥.有横缝高拱坝的非线性地震响应分析［D］.成都：四川大学，2002.