中考中开放探究型问题解读
☉浙江宁波市北仑区梅山中学 王 浩
开放探究型问题具有较强的综合性与创造性,既能考查同学们对基础知识的掌握,又能反映同学们对知识内容的拓展、联想应用能力和开发创造能力,培养同学们的发散思维能力和空间想象能力,同时体现了同学们学习的自主性,成为考试中的热点内容.笔者对开放性问题的几种类型做了一个归纳,希望能给同学们的学习带来帮助.
一、条件开放探究类型
条件开放类问题一般给出部分条件和结论,添加适当条件可以推论出结论.要求同学们能全面理解题目的知识背景,探究结论成立的条件,往往满足的条件不唯一.
例1 如图1,△ABC中,CD⊥AB,垂足为D.下列条件中,能证明△ABC是直角三角形的有__________(多选、错选不得分).



点评:条件开放探究型问题一般难度不大,但有一定开放度,所以在探究结论成立的条件时,答案可能不唯一,思维的方向是多角度的.本题中是从直角三角形的定义、勾股定理的逆定理和相似三角形性质三个角度来进行设计问题,这样的问题可以培养同学们的发散思维能力和综合应用知识的能力.
二、结论开放探究类型
结论开放探究类型问题特点是题设中给出全部条件,要求同学们能分析条件并探究由所给条件猜想出可以得出哪些结论,并证明所猜想的结论是否正确.由于所要证明的目标不明确,要求同学们具有综合分析判断能力和科学的推断论证能力.
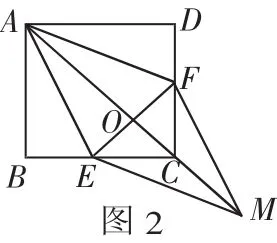
例2 已知:如图2,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.
(1)求证:BE=DF.
(2)连接AC交EF于点O,延长OC至点M,使OM=OA,连接EM、FM.判断四边形AEMF是什么特殊四边形,并证明你的结论.
分析:问题(1)中,可通过Rt△ABE与Rt△ADF全等证明BE=DF;在问题(2)中,根据条件和正方形的性质,可以得到OE=OF,OA=OM,所以四边形AEMF是平行四边形.又AE=AF,可根据菱形的判定得出四边形AEMF是菱形.
解:(1)因四边形ABCD是正方形,则AB=AD,∠B=∠D=90°.
因AE=AF,所以Rt△ABE≌Rt△ADF,所以BE=DF.
(2)因四边形ABCD是正方形,
则∠BCA=∠DCA=45°,BC=DC.
因BE=DF,所以BC-BE=DC-DF,即CE=CF.则OE=OF.
因OM=OA,所以四边形AEMF是平行四边形.
因AE=AF,所以平行四边形AEMF是菱形.
点评:结论开放类型问题探究问题的目标不具体,要求同学们能结合条件作出科学的猜想和论证.本题问题(2)中以正方形图形为知识载体创设问题探究环境,猜想的过程中也是论证与推理的统一过程.从图形中不难发现四边形AEMF是菱形,接下来要联系条件与第(1)问题结论进行论证.
三、条件与结论全开放探究类型
一个问题中条件与结论同时开放时,问题的开放度较大,对同学们能力水平要求较高,能从所给选项中组织条件,创设问题并能解决问题.
例3 如图3,点D,E在△ABC的边BC上,连接AD,AE.①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,构造三个命题,并回答下列问题:
(1)构造的命题是(用序号表示)______;
(2)以上三个命题是真命题的为
(直接作答)__________;
(3)请选择一个真命题进行证明
(先写出所选命题,然后证明).
分析:本题中有三个选项,由其中两个作为条件.第三个作为结论,共有3种组合方法,即(1)①②⇒③;①③⇒②;②③⇒①;所组合的三个命题都是真命题.在命题(1)中,条件是AB=AC,AD=AE,说明△ABC,△ADE都是等腰三角形,可以通过证明△ABD,△ACE全等,得到BD=CE;在命题(2)中,条件是AB=AC,BD=CE,所以△ABC是等腰三角形,所以有∠B=∠C,可证明△ABD,△ACE全等得到AD=AE;在命题(3)中,条件是AD=AE,BD=CE,所以有∠ADB=∠AEC,所以△ADB≌△AEC,可证AB=AC.
解:(1)①②⇒③;①③⇒②;②③⇒①;
(2)(1)①②⇒③;①③⇒②;②③⇒①;
(3)证明命题(1).
因AB=AC,则∠ABC=∠ACB.
因AD=AE,则∠ADC=∠AEB,则∠ADB=∠AEC.
在△ABD与△ACE中,AB=AC,∠ABC=∠ACB,∠ADB=∠AEC,则△ABD≌△ACE,则BD=CE.
点评:条件与结论同时开放问题的开放度较大,要求同学们能对所有的选项进行组合,构建问题并能推理认证.本问题中,主要依据三角形的全等来证明线段的相等,不同的构造方法证明方法也不一致,所构造的三个命题全是真命题.
开放探究型问题题型设计灵活,问题所涉及知识面广,要求同学们具有较强的解题能力和思维能力,所以此类题目已成为近年来中考试题的热点题.


