等腰三角形一条性质的多种证明与拓展
☉河南省漯河市外语中学 龚天芝
等腰三角形底边上任意一点到两腰的距离和等于一腰上的高.
已知:如图1,在△ABC中,AB=AC,点P是边BC上任意一点,PE⊥AB,PF⊥AC,CD⊥AB,垂足分别是E、F、D.
求证:PE+PF=CD.
证法1(面积法):



故等腰三角形底边上任意一点到两腰的距离和等于一腰上的高.
证法2(截长法):
在CD上截取DG=EP,连接PG,如图2.
因为CD⊥AB,PE⊥AB,
所以四边形DEPG是矩形,所以∠DGP=90°.
因为AB=AC,所以∠B=∠ACB.
因为GP//DE,所以∠GPC=∠B.
所以∠ACB=∠GPC,又因为PC=CP,∠PGC=∠CFP=90°.
所以△CGP≌△PFC,所以PF=CG.
所以PE+PF=DG+GC=CD.
证法3(补短法):
延长EP到G,使EG=DC,连接CG,如图3.
因为CD⊥AB,PE⊥AB,

所以四边形DEGC是矩形,所以∠G=90°.

因为AB=AC,所以∠B=∠ACB,
因为GC//DE,所以∠GCP=∠B.
所以∠ACB=∠GCP,又因为PC=PC,∠G=∠CFP=90°.
所以△CGP≌△CFP,所以PF=PG.
所以PE+PF=EG=CD.
(过点P作PG⊥CD,垂足为G,可得矩形DEPG,如图2,以下证法同方法2,可使问题得证;过C作直线EP的垂线,垂足为G,可得矩形DEGC,如图3,以下证法同方法3,可使问题得证.)
证法4(利用三角形相似):
因为PE⊥AB,PF⊥AC,CD⊥AB,如图1.
所以∠BEP=∠BDC=∠CFP=90°.
因为AB=AC,所以∠B=∠ACB.
所以△BEP∽△BDC∽△CFP.


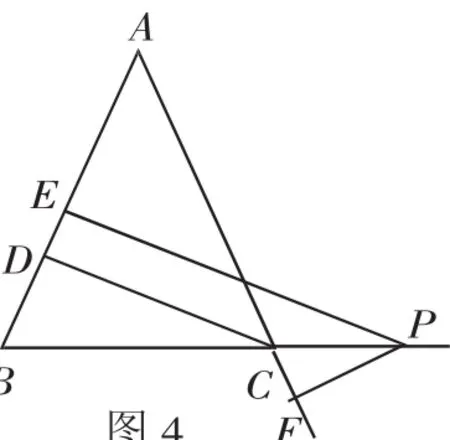
拓展1.如果P在BC(或CB)的延长线上,如图4,有下列结论:|PE-PF|=CD.(证明方法同上,过程略)
即:等腰三角形底边延长线上任意一点到两腰的距离差等于一腰上的高.
拓展2.如果把等腰三角形变为等边三角形,又有如下结论:
已知等边△ABC和点P,P到△ABC的三边AB、AC、BC的距离分别为h1、h2、h3,△ABC的高为h.
(1)当点P在△ABC的一边BC上时,如图5,此时h3=0,则h1+h2+h3=h.
即:等边三角形边上一点到三边的距离和等于等边三角形的高.
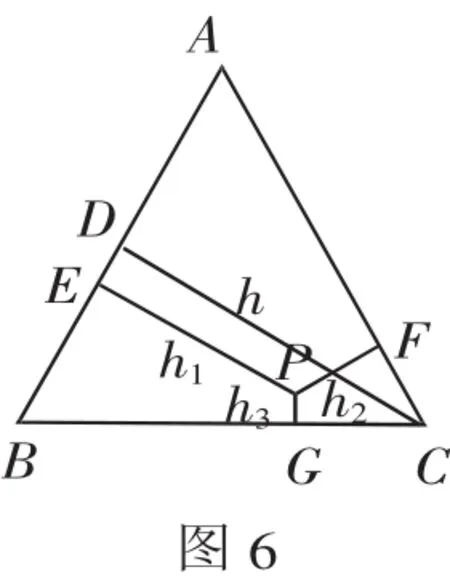
(2)当点P为△ABC内任意一点时,如图6,结论h1+h2+h3=h仍成立.
即:等边三角形内任意一点到三边的距离和等于等边三角形的高.
由此可知,在等边三角形ΔABC中,设O为其中心,O到一边的距离为r3,显然h=3r3,就有结论h1+h2+h3=3r3
(3)当点P在△ABC外部时,如图7,可得h1+h2-h3=h.
(证明方法同上,过程略)
拓展3.如果把等边三角形变为正方形、正五边形,正n边形时,又有如下结论:
若点P为正边形ABCD内任一点,点O为正方形的中心,O到一边的距离为r4,P点到AB、BC、CD、DA各边的距离为h1,h2,h3,h4,则h1+h2+h3+h4=4r4.
若点P为正五边形ABCDE内任一点,点O为正五边形的中心,O到一边的距离为r5,P到AB、BC、CD、DE、EA各边的距离为h1,h2,h3,h4,h5,则h1+h2+h3+h4+h5=5r5.
若点P是正n边形内任一点,O是正n边形的中心,点O到一边的距离为rn,点P到各边的距离分别为h1,h2,h3,…,hn,则h1+h2+h3+…+hn=nrn.(证明略)
中考链接



例1(2009辽宁朝阳)如图8,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=2,则DE+DF=_______.
解析:由等边三角形的性质可知“等边三角形一边上任意一点到其他两边的距离和等于等边三角形的高”,可求得
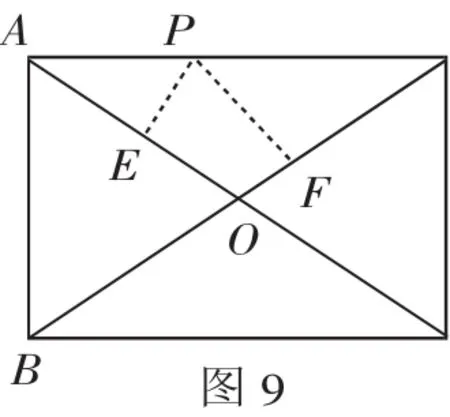
例2 (2011山东聊城)如图9,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( ).


例3(2011年佳木斯)如图10,将矩形纸片ABCD沿对角线AC折叠,使点B落到点B′的位置,AB′与CD交于点E.
(1)试找出一个与△AED全等的三角形,并加以证明.
(2) 若AB=8,DE=3,P为线段AC上的任意一点,PG⊥AE于G,PH⊥EC于H,试求PG+PH的值,并说明理由.
解析:(1)由∠D=∠B′=90°,∠AED=∠CEB′,AD=CB′,可证△CEB′≌△AED.
(2)由题意易证△ACE是等腰三角形,因此根据等腰三角形的性质可知PG+PH=AD.在Rt△ADE由勾股定理得AD=4,即PG+PH=4.

例4 (2011年河北省)在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图11-1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.
(1)在图11-1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想.
(2)当三角尺沿AC方向平移到图11-2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想.
(3)当三角尺在(2)的基础上沿AC方向继续平移到图11-3所示的位置(点F在线段AC上,且点F与点C不重合)时,(2)中的猜想是否仍然成立?(不用说明理由)
解析:(1)BF=CG.在△ABF和△ACG中,由∠F=∠G=90°,∠FAB=∠GAC,AB=AC,可证△ABF≌△ACG(AAS),故BF=CG.
(2)根据等腰三角形的性质“等腰三角形底边上任意一点到两腰的距离之和等于一腰上高的长.”可证DE+DF=CG.
(3)仍然成立.




