二元传递关系计数的上界估计

董永红 郭海林 刘智秉

(1 九江学院理学院; 2 九江学院图书馆 江西九江 332005)

1 预备知识

定义1［1］若S⊆R ×R，则称S为R上的一个二元关系.称S对应的m阶(0，1)矩阵A =(aij)m×m为S的关联矩阵，即(ai，aj)∈S，aij =1;(ai，aj)∉S，aij =0.

定义2［2］给定一个二元关系S，S对应一个有向图Γ，称Γ 为S的对应图.图Γ的顶点集为R ={ai|i =1，2，…，m}，边集为E ={eij=aiaj|(ai，aj)∈S}.

定义3 给定一个二元关系S，记RS ={ai∈R|∃aj∈R，s.t. (ai，aj)∈S}.称|RS|为关系S涉及R的元素个数.一般|RS|≤m =|R|.若|RS|=m称S为二元全涉关系，此时关系对应的矩阵称为全涉矩阵，对应的图为全涉图.依据图论知识，有向图的边集是一个多重子集，而二元关系是单重子集，因此二元关系的对应图是没有重边的.

文献［4］的完全计数是考虑有限集R中元素的次序下，满足某些性质的二元关系的计数.若不考虑有限集R中元素的次序，笔者发现二元关系对应的关联矩阵满足交换行列的合同变换，称为置换合同，即:B=PAPT，其中P为置换矩阵，PT表示P的转置.易见这种合同变换是全体关联矩阵上的一个等价变换，由此本文将关联矩阵合并成等价类，来讨论二元关系的等价类计数.特别是结合关联矩阵与有向图的关系，估计出二元传递关系的等价类计数的一个上界.

2 主要结论

定理2 二元传递关系的等价类计数记为qm，其一个上界为Lm:

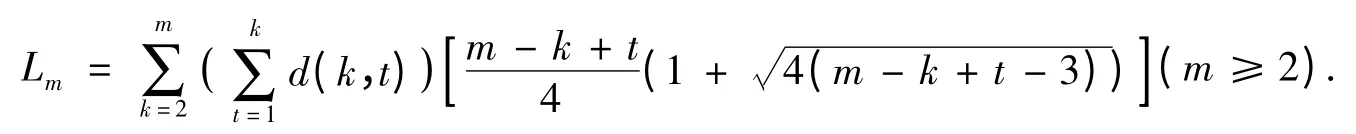
其中［x］表示对实数x下取整.

证明定理2 时，需要转化为有向图来讨论，在此处介绍两个命题.

命题1 若二元传递关系对应的图是圈，则涉及n个点的圈是一个有向圈.

证明:如果二元传递关系对应的涉及n个点的圈为a1→a2→a3→…→an→a1，那么对任意的i，j有ai→aj，aj→ai.不妨设i≤j≤n，当i ＜j时，有aij=aji =1;当i=j时，由传递性知ai(i+j)=a(i+j)i =1，有aii =1.由此圈上的每个点都带有自环，且每条边都是双向的，易见这种圈对应的矩阵为全1 阵.如果传递关系对应的有向图中有圈，那么将这样的圈看成一个点或压缩为一点，并不改变原图的连通性.由此我们来构造新的有向图.

例如对图Γ=(V，E)，V为图的顶点，E为图的边.用ai，aij分别表示原图Γ的顶点和边，用a'i，a″ij分别表示新图Γ'的顶点和边.

若图Γ的顶点集为:

则新图Γ'的顶点集为:

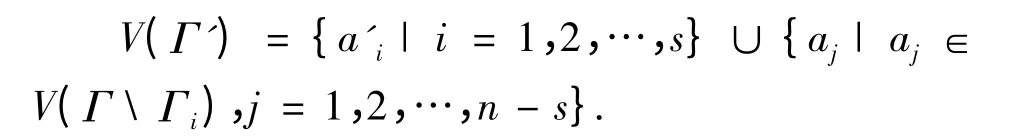
其中V(Γ1)，V(Γ2)，…，V(ΓS)为有向圈上的点集，V(Γ Γi)为原图减去所有有向圈后余下的顶点集.这样原图中的顶点集V(Γi)在新图中被压缩成一个点a'i.

上述方法构造的新图与原图有命题2 描述的性质.

命题2 若图Γ'是图Γ 构造的，则新图不改变原图的连通性.此处的连通性是指:①图Γ 中的有向圈与其分支的连通性;②图Γ 中除去有向圈后剩余点的连通性;③圈与圈之间的连通性.

证明:

(1)设图Γ 中的一个有向圈为Γ1=(V1，E1).假设ak∉V1，若ai∈V1，使得aki =1，则对任意的aj∈V1，有akj=akiaij =1.同样的，若ai∈V1，使得aik=1，则对任意的aj∈V1，有ajk=ajiaik =1.若原图中顶点集V1中有许多点与ak相连，而新图Γ'是将V1压缩成一点与ak相连，因此这种压缩不改变图的连通性.即图Γ 中的有向圈与其分支的连通性.

(2)设图Γ 中所有圈的顶点集合为V1，V2，…，Vs.图Γ的顶点为:

其中i =1，2，…，s;(VVi)表示图Γ 减去所有圈余下的顶点集，w1∈V1，w2∈V2，…，ws∈Vs.

如果对任意的ai，aj∈(VVi)，有边aiaj∈E(Γ)，那么新图Γ'中有边aia'j并且aia'j=aiaj.即圈外的点的连通性Γ'与Γ 是一致的.

(3)若顶点wi∈Vi，wj∈V，任取ai∈Vi，aj∈Vj有wij=aij =1，在新图Γ'中表现为一个圈被压缩成一个点.于是图Γ 中的s个圈被压缩为s个点，此时s个圈的连通性被简化成s个点的连通性，因此新图Γ'与原图Γ的连通性是一致的.

为了方便刻画二元关系的计数，笔者引入一个引理.

其中［x］表示对实数x下取整.

［1］Martin Aigner and Gunter M Ziegler. Proofs from the book (3rd edition.) ［M］. Berlin: Springer-Verlag Heidelberg，2004. 26.

［2］Reinhard Diestel. Graph Theory ［M］. Berlin: Springer-Verlag Heidelberg，2006. 13.

［3］刘丁酉. 矩阵分析［M］. 武汉: 武汉大学出版社，2003. 27.

［4］董永红，朱一心，石富华. 二元关系的完全计数［J］. 数学的实践与认识，2011，41(24) : 217.