基于古塔变形预测的数学模型

陈卫忠，王 庆

(苏州市职业大学 数理部，江苏 苏州 215104)

1 问题提出

在中国辽阔美丽的大地上，古塔形成了一种具有中国民族传统特色的建筑类型.由于长时间承受自重、气温、风力等各种作用，偶然还要受地震、台风的影响，古塔会产生各种变形，诸如倾斜、弯曲、扭曲等.为保护古塔，文物部门需适时对古塔进行观测，了解各种变形量，以制定必要的保护措施.

本文参照2013高教社杯全国大学生数学建模竞赛D题，某管理部门委托测绘公司于1986年7月、1996年8月、2009年3月和2011年3月对我国重点保护文物某古塔进行的4次数据观测[1]，提出下列3个问题：

问题1，给出确定古塔各层中心位置的通用方法；

问题2，分析该塔倾斜、弯曲、扭曲等变形情况；

问题3，分析该塔的变形趋势.

本文对这3个问题，力求通过对观测数据进行分析，建立数学模型，并通过模型预测古塔的变形趋势.

2 问题分析和模型假设

为解决以上3个问题，通过对所列数据的分析，对3个问题分别作分析和模型假设.

对问题1，由于题目提供的观测数据有缺失，考虑用外推法或几何方法补充1986年和1996年缺失的数据(古塔第13层第5点).确定古塔各层中心位置时，考虑各层基本处于同一平面内，可先拟合出各层所在平面，将各测量点投影到拟合平面内，然后再用均匀物体的重心公式[2]计算中心坐标.

对问题2，要分析该塔倾斜、弯曲、扭曲等变形情况，可对各层中心点作线性拟合[3]，中轴线与水平面法向的夹角可作为倾斜程度的度量.对各层中心点作曲线拟合，曲线上各点曲率的平均值可作为弯曲程度的度量.相邻两个平面的旋转角度可作为扭曲程度的度量.

对问题3，可利用问题2中的各种变形，关于时间作拟合，推测未来几年的变化情况.

3 模型的建立和求解

3.1 对问题1模型的建立和求解

首先对缺失数据进行处理，将1986年和1996年古塔的第13层其他点的观测数据的平均值，作为缺失的第5点的数据.通过Matlab作出图1，分析观测数据的分布.由图1可以直观地看出古塔各层的观测点不在同一平面上，因此要求出古塔各层的中心位置坐标，需先拟合出各层观测点所在平面.设平面π：Ax+By+Cz+D=0，则该层的第i个观测点Qi(xi，yi，zi)到平面π的距离.利用最小二乘法，求出使该层上所有观测点到平面π的距离之和最小时的系数A、B、C，拟合出平面π.

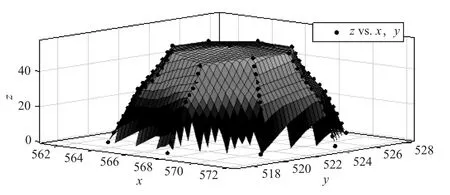
图1 观测数据的分布图

再将各观测点Qi(xi，yi，zi)投影到平面π内，得到投影点，求出的坐标.平面π的法向量为n=(A,B,C)，则向量，即，又因为π∈ ，所以，则，从而得

最后，古塔各层中心坐标用均匀物体的重心公式计算.如图2所示，n边形A1A2…An，顶点坐标A1(x1，y1)，A2(x2，y2)，…，An(xn，yn)，连接A2An，A3An，…，An-2An，得到n-2个三角形：△A1A2An，△A2A3An，…，△An-2An-1An，它们的重心为其中，面积为σi，i=1，…，n-2，则n边形A1A2…An的 重心为G(x,y)，其中：

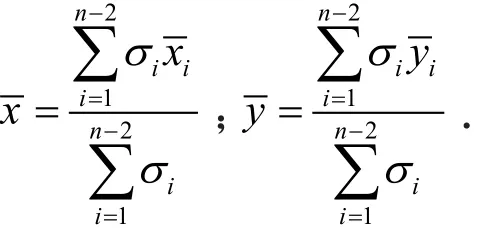
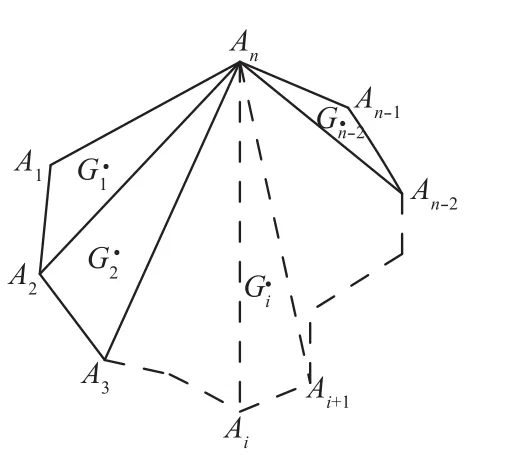
图2 重心公式计算图

3.2 对问题2模型的建立和求解

利用Matlab画出每年古塔各层的中心位置分布图，如图3所示，发现古塔发生倾斜和弯曲，各层的中心点不共线、也不共面.

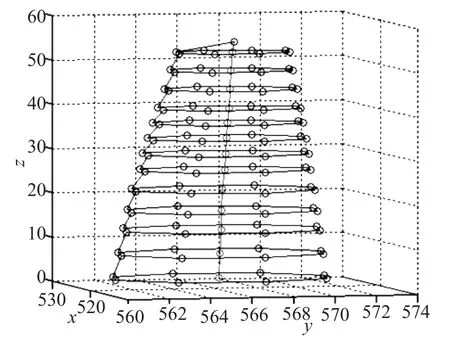
图3 中心位置分布图

利用问题1求拟合平面及投影点.首先求出到各层中心点距离之和最小的平面π'，再将第i层中心点Qi(xi，yi，zi)，i=1，…，13，投影到平面π'：A'x+B'y+C'z+D'= 0 上，得到投影点，其中.再在平面π'内选取O1'作为坐标原点，O1'与O2'的连线O1'O2'作为X轴，过O1'作O1'O2'的垂线作为Y轴，过O1'作平面π'的垂线作为Z轴，得到空间坐标系O1'XYZ，则各层中心点在平面π'的投影点在空间坐标系O1'XYZ的坐标为

分析该塔倾斜程度.在平面π'上对各层中心点的投影点作线性拟合，平面π'的法向量与Z轴的夹角θ可作为倾斜程度的度量.设各层中心点的投影点在平面π'上拟合的直线方向向量为{l，m，n}，则

分析该塔弯曲程度.在平面π'上对各层中心点的投影点作曲线拟合，曲线上各点曲率的平均值可作为弯曲程度的度量.设拟合的曲线方程为y=f(x)，曲线上各点曲率，则古塔的弯曲程度的度量为

分析该塔扭曲程度.相邻两个平面的旋转角度可作为扭曲程度的度量.将古塔相邻两层的观测点投影到坐标面上.如图4所示，某个观测点的扭曲可用α表示，则

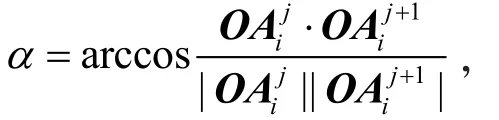
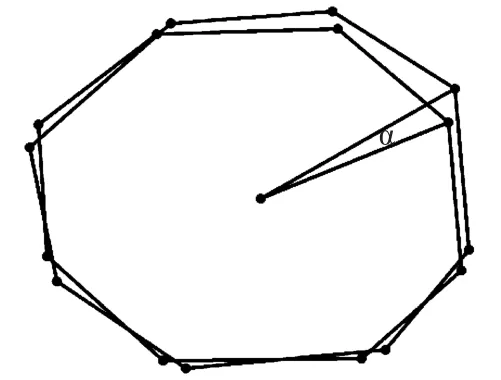
图4 观测点投影图

其中O表示第j层上第i个观测点投影到坐标面上的向量.求出所有观测点的扭曲，取平均值作为古塔相邻两层的扭曲.

3.3 对问题3模型的建立和求解

为了分析古塔的变形趋势，在问题2的基础上将古塔倾斜角度、弯曲率、扭曲度关于时间作拟合，推测未来几年的变化情况.

1)古塔倾斜角度的时间拟合.由图5可见，从1986年到1996年，古塔的倾斜角增加较大；2011之后古塔的倾斜角变化不大.

2)古塔弯曲率的时间拟合.由图6可见，从1990年到1996年，古塔的弯曲较严重，而1996年到2009年，古塔的弯曲率逐年减小，2011年之后古塔的弯曲变化不大.

3)古塔扭曲度的时间拟合.由图7可见，从1986年到2011年，古塔的扭曲度逐年增大，预计之后几年内古塔的扭曲度趋于平稳.

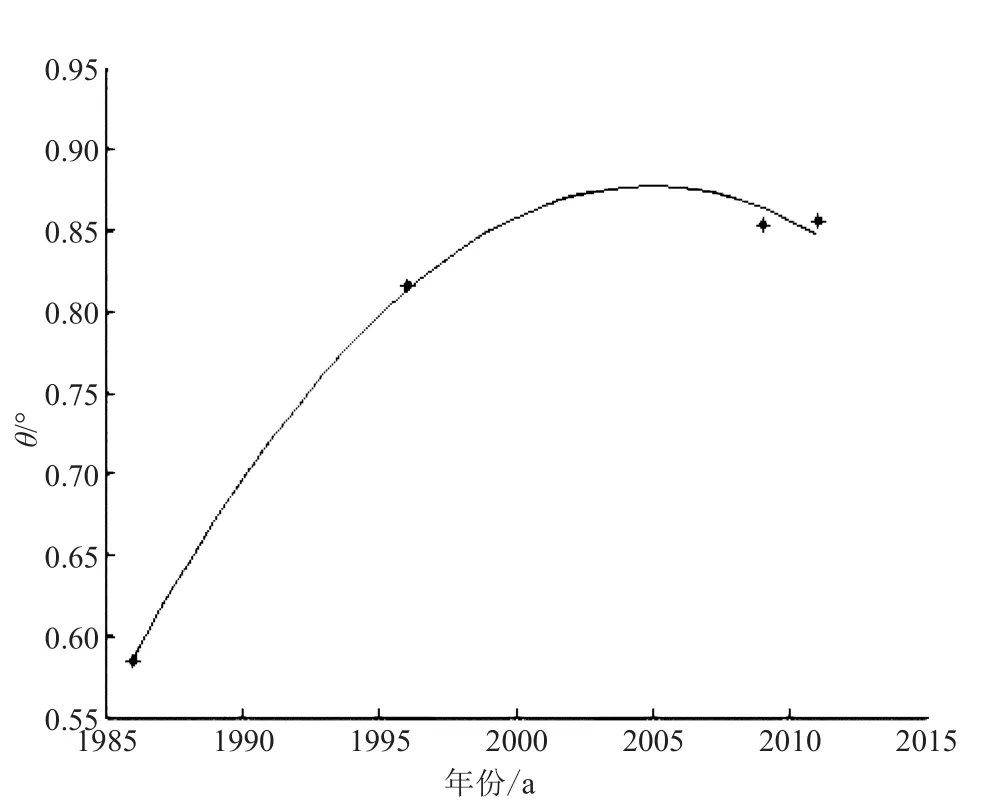
图5 古塔倾斜角度的时间拟合图

4 结论

图6 古塔弯曲率的时间拟合图

图7 古塔扭曲度的时间拟合图

通过文中给出确定古塔中心位置的方法，对古塔倾斜、弯曲、扭曲等变形情况进行度量分析，古塔变形的原因和趋势是：随着时间的累积，古塔有变形迹象、沉降趋势，这与古塔的高度有关系，同时受外界自然风力、地震等的影响，也直接影响到古塔的扭曲、弯曲情况，所以建议有关部门定期对古塔进行检测维修.这一模型除了用于对古塔等古建筑的维护外，还可以对现代高楼大厦的维护提供指导性方法[4].

[1]教育部高等教育司，中国工业与应用数学学会. 中国大学生数学建模竞赛[EB/OL]. (2013-09-09)[2014-02-09].http：//www.mcm.edu.cn/html cn/node/a l ffc4c5587c8a6f96eacefb8dbcc34e.html.

[2]向爱琴. 质面多边形重心公式的再探讨[J]. 新疆教育学院学报，1989(1)：58-60.

[3]龚杨. 空间直线拟合的一种方法[J]. 齐齐哈尔大学学报，2009(2)：64-67.

[4]梁海奎. 古塔变形测量方法探讨[J]. 城市勘探，2011( 3)：113－118.