基于n阶算子的面向对象概念格压缩

万家良，魏 玲

(西北大学数学系，陕西西安 710127)

Wille R.于1982年提出的形式概念分析理论[1－2]是一种非常有力的数据分析和知识发现的数学工具，广泛应用于人工智能和信息检索等领域[3－4]。

粗糙集理论和概念格理论是两种不同的知识处理的数学工具。近年来，广大学者对概念格和粗糙集理论展开了深入的研究，并且将二者结合起来，以便更好地掌握和理解数据[5－6]。Duntsch和Gediga通过定义modal-style算子，并且由粗糙近似算子构造了面向属性概念格[7]，Yao Y.Y.借用该思想，建立了面向对象概念格，且证明了面向属性概念格与面向对象概念格是同构的[8]，为数据分析提供了新的理论依据。

随着网络的发展，大数据时代离我们越来越近，从庞大的数据库中找到我们需要的知识越来越困难，构建概念格也变得十分复杂。因此，概念格的压缩引起了人们的关注。文献[9]用SVD对概念格进行剪枝的方法，使原概念格的结构变小。文献[10]应用FKM-模糊聚类方法对概念格进行压缩，减少了概念格的节点。但是，这两种方法都是对经典概念格进行压缩。文献[11]根据对象的相似程度调整对象邻域的大小，控制面向属性概念格的节点，对面向属性概念格进行压缩。而本文则是从面向对象概念出发，借鉴文献[12－13]的n阶粗糙集的思想，引入n阶算子，产生n阶面向对象概念，进而通过调整n值的大小，对面向对象概念格进行动态压缩，并给出压缩后的概念与原面向对象概念格概念的关系，达到简化知识库的目的。

1 预备知识

定义1[1]称三元组(G，M，I)是一个形式背景，其中 G={x1，x2，…，xn}为对象集，每个 xi称为一个对象，M={a1，a2，…，as}为属性集，每个ai称为一个属性，I是对象集G和属性集M之间的二元关系集，且I⊆G×M。若(x，a)∈I，则称x具有属性a。

对于形式背景(G，M，I)，在对象集X⊆G和属性集B⊆M上分别定义运算* 与'[1－2]:

X*={a|a∈M，∀x∈X，(x，a)∈I}，

B'={x|x∈G，∀a∈B，(x，a)∈I}。

X*表示X中所有的对象共同具有的属性集合，B'表示具有B中所有属性的对象集合。若∀x∈G，x*≠∅，x*≠M，且∀a∈M，a'≠∅，a'≠G，则称形式背景(G，M，I)是正则的，以下假定形式背景都是正则的。

文献[8]用“□”表示下近似对应的集合，用“◇”表示上近似对应的集合，对于X⊆G及B⊆M，定义

X□={a∈M|a'⊆X}，

B◇={x∈G|x*∩B≠∅}。

定理 1[8]设(G，M，I)为一个形式背景，∀X，X1，X2⊆G及∀B，B1，B2⊆M，算子“□”与“◇”有以下性质:

1)X1⊆ X2⇒X1□⊆X2□

2)B1⊆ B2⇒B1◇⊆B2◇;

3)X□◇⊆X，B⊆B◇□;

4)X□◇□=X□，B◇□◇=B◇;

5)(X1∩X2)□=X1□∩X2□，(B1∪B2)◇=B1◇∪B2◇。

定义 2[8]设(G，M，I)是形式背景，如果∀X⊆G，∀B⊆M，满足X=B◇且B=X□，则称二元组(X，B)为面向对象概念。其中X为概念的外延，B为概念的内涵。

定理 2[8]设(G，M，I)是形式背景，记LO(G，M，I)={(X，B)|X=B◇，B=X□}，令(X1，B1)≤(X2，B2)，则LO(G，M，I)为偏序集。在LO(G，M，I)上定义

(X1，B1)∧ (X2，B2)=((X1∩ X2)□◇，B1∩B2)，

(X1，B1)∨ (X2，B2)=(X1∪ X2，(B1∪B2)◇□)，

那么(LO(G，M，I)，∨，∧)是一个完备格，称为面向对象概念格。

把所有面向对象概念的外延的集合表示为LOG(G，M，I)，所有面向对象概念的内涵的集合表示为 LOM(G，M，I)。

定义3[1]设(G，M，I)为形式背景，对于它的两个概念(Xi，Bi)和(Xj，Bj)，若 Xi⊆ Xj或 Bi⊆ Bj，则称(Xi，Bi)是(Xj，Bj)的亚概念，(Xj，Bj)是(Xi，Bi)的超概念。

定义 4[14－15]设(G，M，I)为形式背景，对于它的两个概念(X1，B1)，(X2，B2)，若(X1，B1)≤(X2，B2)，而且不存在(X，Y)，(X，Y)≠ (X1，B1)，(X，Y)≠ (X2，B2)，使 得(X1，B1)≤ (X，Y)≤ (X2，B2)，则称(X1，B1)是(X2，B2)的子概念，称(X2，B2)是(X1，B1)的父概念。

2 面向对象概念格的压缩

本文提出的面向对象概念格的压缩方法是通过引入n阶上下近似算子，产生n阶面向对象概念，进而由n值的大小来控制压缩后的节点个数，最终实现对面向对象概念格的动态压缩。

2.1 压缩方法

定义5 设(G，M，I)为形式背景，对于X⊆G及B⊆M，定义算子“□n”与“◇n”如下:

X□n={a∈ M||a'－ X|≤ n}=

{a∈ M||a'|－|a'∩ X|≤ n}，

B◇n={x∈G||x*∩B|＞ n}。

n=0，1，…，max{|G|－1，|M|－1}，|·|表示集合的基数。

定义5表明，如果具有属性a的对象个数最多有n个不在对象集X中，则属性a属于X□n;如果对象x所拥有的属性在属性集B中的元素个数多于 n个，则对象x属于B◇n。

定理3 设(G，M，I)为一个形式景，∀X，X1，X2⊆ G及 ∀B，B1，B2⊆ M，算子“□n”与“◇n”有以下性质:

1)X□0=X□;B◇0=B◇;

2)∅◇n= ∅，G□n=M;当n≠0时，a◇n=∅;

3)X1⊆X2⇒

4)(X1∩ X2)□n⊆

5)若 n≥ m，则:X□n⊇ X□m，B◇n⊆ B◇m;

证 明 1)，2)可直接由定义得出。

3)∀a∈X1□n，有|a'－ X1|≤ n。如果X1⊆X2，则 |a'－X2|≤ |a'－X1|≤n，所以a。因此有。第二式可类似证明。

4)因为X1∩X2⊆ X1，X1∩X2⊆ X2，所以由3)可知:(X1∩X2)□n⊆X1□n，(X1∩ X2)n⊆，于是，(X1∩ X2)□n⊆ X1□n∩。类似地，(B1∪B2)◇n

5)∀a∈ X□m，有|a'－ X|≤ m。如果 n≥m，则 |a'－ X|≤m≤n，即a∈X□n。因此，X□n⊇X□m。∀x∈B◇n，有|x*∩B|＞ n。如果n≥m，则|x*∩B|＞ n≥m，即x∈B◇m。

对比定理1发现，算子“□n”与“◇n”不具备类似于定理1中的性质3)和性质4)，这可通过下面的例题得出。

例1 设形式背景(G，M，I)如表1所示，对象集G={1，2，3，4，5，6}，属性集M={a，b，c，d，e，f}。其中 × 表示(x，a)∈ I。其面向对象概念格如图1所示。为简便起见，本文中内涵与外延皆用相应集合的元素序列表示。

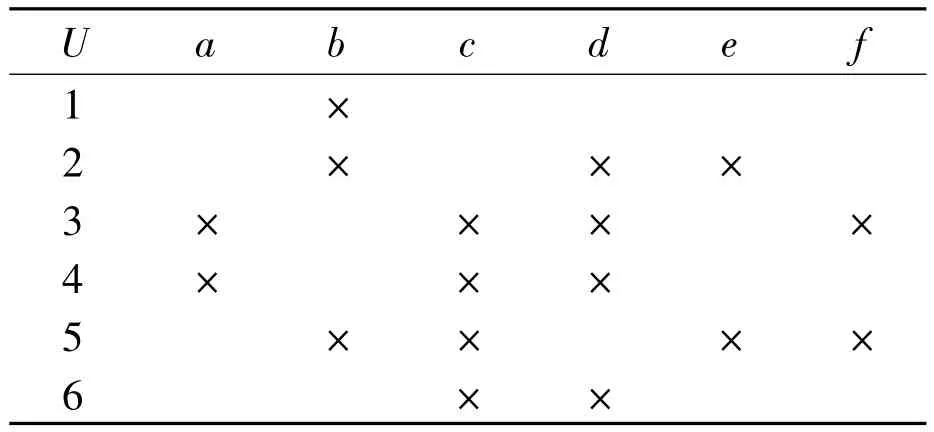
表1 形式背景T=(G，M，I)Tab.1 T=(G，M，I)

图1 LO(G，M，I)Fig.1 LO(G，M，I)

不失一般性，这里取n=1。

令 X=3456，则

X□1={a∈M||a'－ 3456|≤1}=acdef。而 X□1◇1=acdef◇1={x∈G| |x*∩acdef| ＞1}=23456。同时 X□1◇1□1=23456□1=M。所以X□1◇1⊄ X，X□1◇11≠ X1。

令 B=ad，则B◇1={x∈G| |x*∩ad|＞ 1}=34。

而 B◇1□1=34□1={a∈ M||a'－ 34|≤1}=af。同时 B◇1□1◇1=af◇1=3。所以 B ⊄ B◇1□1，B◇1□1◇1≠ B◇1。

为便于下文叙述，记

O(G，M，I)={∩Xi∈XXi|X ⊆ LOG(G，M，I)}，

A(G，M，I)={∪Bi∈BBi|B ⊆ LOM(G，M，I)}。

定义6 设LO(G，M，I)是面向对象概念格。若X=B◇n，B=X□n，n ＞ 0，则称(X，B)为压缩后的n阶面向对象概念。

定义6即是将原面向对象概念的内涵压缩为一些概念内涵的并，将原面向对象概念的外延压缩为一些概念外延的交。

例2 本例针对例1中的形式背景，研究n=1及n=2时，面向对象概念格的压缩，以达到简化概念格的目的。

当n=1时，其面向对象概念格的压缩步骤如下:

1)∀X ∈ O(G，M，I)，计算 X□1:

∅□1，= ∅，3□1=34□1=af，

5□1=ef，2□1=e，

35□1=23□1=aef，25□1=125□1=bef，

235□1=1235□1=abef，345□1=acef，

346□1=acdf，

23□1=adef，2346□1=3456□1=acdef，

2345□1=23456□1=12345□1=M。

2)∀B ∈ A(G，M，I)，计算 B◇1:

∅◇1=a◇1=e◇1=f◇1= ∅，af◇1=3，

be◇1=bef◇1=25，aef◇1=35，ef◇1=5，

ad◇1=34，acf◇1=acef◇1=345，

abef◇1=235，

ade◇1=234，adcf◇1=3456，

abcef◇1=abdef◇1=2345，

acdef◇1=M◇1=23456。

3)由定义6可得到压缩后的所有概念:

(23456，M)，(235，abef)，(345，acef)，(35，aef)，(25，bef)，(3，af)，(5，ef)，(∅，∅)。

压缩后的1阶面向对象概念的Hasse图如图2所示。

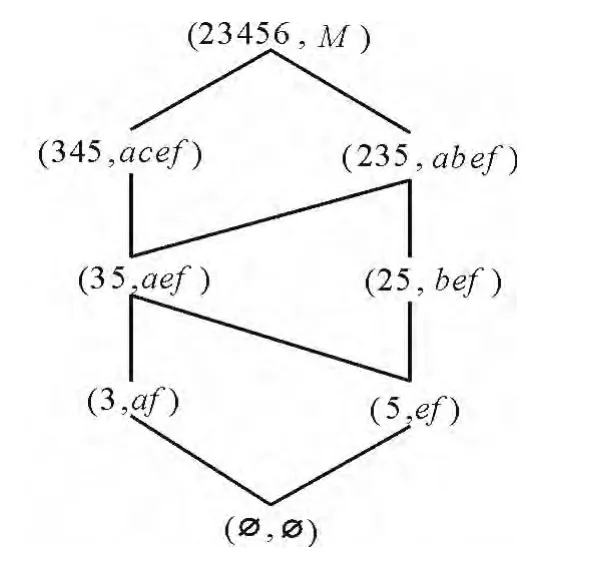
图2 LO1(G，M，I)Fig.2 LO1(G，M，I)

当n=2时，由类似的计算过程可得到2阶面向对象概念，其Hasse图如图3所示。

对比压缩后的n阶面向对象概念的Hasse图与原形式背景的面向对象概念格可知，本文的压缩实质是:如果形式背景中的对象x满足|x*|≤n，则作n阶压缩时，将该对象去掉;如果形式背景中的属性m满足|m'|≤n，则作n阶压缩时，n阶面向对象概念的内涵都有该属性。

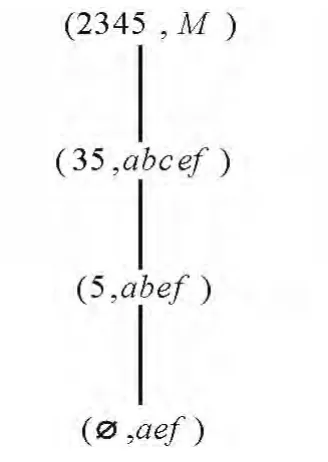
图3 LO2(G，M，I)Fig.3 LO2(G，M，I)

2.2 相关性质

以下两个定理将给出LO(G，M，I)的概念外延和内涵分别作n阶算子后的特征。

定理4 设(G，M，I)为形式背景，∀(X，B)∈ LO(G，M，I)，X ≠ G，(Xi，Bi)是(X，B)的超概念。如果 |Xi|－|X|≤ n(i∈ τ)，则:X□n= ∪τBi。

证 明 因X ⊆Xi，且|Xi|－|X|≤n，所以 ∀a ∈ Bi，有 a'⊆ Xi，因此 |a'－ X|≤ n，即 a∈ X□n，所以Bi⊆ X□n。由i的任意性得，∪τBi⊆X□n。

下面证明 X□n⊆∪τBi。如果 X□n⊄ ∪τBi，那么∃d0∈ X□n，且 d0∉ ∪τBi，即 d0∈ M －∪τBi。由于 |d0'－X|≤n，记C1=d0'－X，D1={d∈M|d'－X⊆C1}，则有d0∈D1。下面证明序对(X∪C1，B∪D1)是一个面向对象概念。由于∀x∉X∪C1，x*∩(B∪D1)=∅，所以只需对X∪C1中的对象作*算子。∀x∈X∪C1，有x*∩(B∪D1)≠∅;同样地，∀b∉B∪D1，因此也只要对B∪D1中的属性作'算子。∀b∈B∪D1，如果b∈ B，则 b'⊆ X∪C1显然，若b∈D1，由D1的定义可知b'⊆X∪C1;从而(X∪C1，B∪D1)是面向对象概念，而且是(X，B)的超概念，满足|X∪C1|－|X|≤ n，且 d0∈ B∪ D1。这与假设 d0∉∪τBi矛盾。所以 Xn⊆ ∪τBi。综上得 Xn= ∪τBi。

推论1 设(G，M，I)为形式背景，∀(X，B)∈ LO(G，M，I)，X≠G，(Xi，Bi)是(X，B)的父概念，如果 |Xi|－|X|＞ n(i∈ τ)，则 X□n=B。

证 明 如果X□n⊄ B，则∃d0∈M －B，有d0∈X□n，|d0'－ X|≤n。同样地，令C2=d0－ X，D2={d∈M|d'－X⊆ C2}，类似的，由定理4可知，概念(X∪C2，B∪D2)是概念(X，B)的超概念，且|X∪C2|－|X|≤n，与题设矛盾，所以不存在属性d0∉B，且d0∈ X□n。因此X□n⊆ B。又因为 B=X□⊆ X□n。得 X□n=B。

例3 在例1中，概念(235，ef)有5个超概念，它们的外延与该概念的外延关系为:

|1235|=|235|+1，|2345|=|235|+1，

|12345|=|23456|=|235|+2，|G|=|235|+3。

则根据定理4得:

235□1={bef}∪ {aef}={abef}，

235□2={aef}∪{bef}∪{abef}∪{acdef}=M，

235□3=M。

概念(∅，∅)有3个父概念，它们的外延与该概念的外延关系为:

|25|=|34|=|35|=2 ＞0。

因此满足推论1的条件，则根据推论1得

∅□2=∅。

定理5 设(G，M，I)为形式背景，∀(X，B)∈ LO(G，M，I)，X ≠∅，(Xj，Bj)是(X，B)的亚概念，j∈ τ。如果|B|－|Bj|≤n，n ＞ 0，则B◇n= ∩τXj。

证 明 因为B ⊆Bj，且|B|－|Bj|≤n。所以∀x ∈B◇n，有x*∩Bj≠∅，又(Xj，Bj)是面向对象概念，从而x∈Xj。由j的任意性，得B◇n⊆∩τXj。下面证明 ∩τXj⊆ B◇n。如果 ∩τXj⊄ B◇n，那么存在 g0∈ ∩τXj，但 g0∉ B◇n，即 |g0*∩B|≤ n。记D1=g0*∩B，C1={g∈G|g*∩B⊆D1}，则g0∈C1。下面证明序对(X －C1，B －D1)是面向对象概念，因为X－C1⊆X，所以只要对X－C1中的对象作* 算子。∀x∈X－C1，若 x*∩D1≠∅，则x∈ C1，显然矛盾，因此x*∩(BD1)≠∅;同样的，由于B－D1⊆B，所以只要对B－ D1中的属性作'算子。∀b∈B －D1，若b'⊆C1，那么b∈ D1，因此 b'∉X －C1。所以(X －C1，B －D1)是面向对象概念，也是(X，B)的亚概念，且满足|B|－|B － D1|≤n，同时g0∉X － C1，但是由假设 g0∈∩τXj，可知矛盾，故得 ∩τXj⊆ B◇n。得 ∩τXj=B◇n。

推论2 设(G，M，I)为形式背景，∀(X，B)∈ LO(G，M，I)，X≠∅，(Xj，Bj)是(X，B)的子概念。如果 |B|－|Bj| ＞ n(j∈ τ)，则 B◇n=X。

证 明 因为X=B◇，所以B◇n⊆X显然。如果 X ⊄ B◇n，则 ∃g0∈ X，但|g0*∩B|≤n，类似的，记D2=g0*∩B，C2={g∈G|g*∩B⊆ D2}，则g0∈C2。由定理5的证明可知(X－C2，B－D2)是概念(X，B)的亚概念，且满足|B|－|B－D2|≤n，与题设矛盾，所以不存在g0∈X，但g0∉ B◇n，因此 X ⊆ B◇n，综上得 B◇n=X。

例4 在例1中，概念(2345，aef)有6个亚概念，它们的内涵与该概念的内涵关系为

|aef|=|ef|+1=|af|+1，

|aef|=|a|+2=|e|+2=|f|+2，

|aef|=|∅ |+3。

则根据定理5得

aef◇1={235}∩{345}={35}，

aef◇2={235}∩{345}∩{34}∩{35}∩{25}=∅，

aef◇3= ∅。

概念(23456，acdef)有3个子概念，它们的内涵与该概念的内涵关系为

|acdef|－|aef|＞ 1，|acdef|－|ad|＞ 1，

|acdef|－|acf|＞ 1。

因此满足推论2的条件，则根据推论2得

acdef◇1={23456}。

由这两个定理可知，LO(G，M，I)中的概念不管从外延出发还是从内涵出发进行压缩，都能得到压缩后的n阶面向对象概念。也就是说任给一个LO(G，M，I)中的概念，都能找到压缩后的唯一的n阶面向对象概念。

3 结 语

概念格作为一种概念数据分析和知识处理的数学工具，已被广泛应用于众多领域。本文主要研究了基于n阶算子的面向对象概念格压缩方法，根据引入的n阶算子进行压缩，并且压缩后的概念的外延为原概念外延的交集，压缩后的概念的内涵为原概念的内涵的并集。通过这种方法，可动态的压缩面向对象概念格，删减不重要的概念，为知识库的压缩提供了一种新的方法。

[1]WILLE R.Restructuring lattice theory:an approach based on hierarchies of concepts[C]∥RIVAL I.Ordered Sets.Dordrecht:Reidel，1982:445-470.

[2]GANTER B，WILLE R.Formal Concept Analysis[M].New York:Mathematical Foundations Springer-Verlag，1999.

[3]CARPINETO C，ROMANO G.A lattice conceptual clustering system and its application to browsing retrieval[J].Machine Learning，1996，10:95-122.

[4]CHEN Y，YAO Y.A multiview approach for intelligent data analysis based on data operators[J].Information Sciences，2008，178(1):1-20.

[5]HU K，SUI Y，LU Y，et al.Concept approximation in concept lattice [J].Lecture Notes in Computer Science，2001，2035:167-173.

[6]KENT R E.Rough concept analysis:a synthesis of rough sets and formal concept analysis[J].Fundamenta Informaticae，1996，27:169-181.

[7]DUNTSCH I，GEDIGA G.Approximation operators in qualitative data analysis[C]//Theory and Application of Relational Structures as Knowledge Instruments.Heidelberg:Springer，2003.

[8]Yao Y Y.A comparative study of formal concept analysis and rough set theory in data analysis[J].Lecture Notes in Artificial Intelligence，2004，3066:59-68.

[9]CHEUNG K S K，VOGEL D.Complexity reduction in lattice based information retrieval[J].Information Retrieval，2005，8:285-299.

[10]ASWANI KUMAR CH，SRINIVAS S.Concept lattice reduction using fuzzy K-Means clustering[J].Expert Systems with Applications，2010，37(3):2696-2704.

[11]魏玲，李强.面向属性概念格基于覆盖的压缩[J].电子科技大学学报，2012，41(2):299-304.

[12]YAO Y Y，LIN T Y.Generalization of rough sets using modal logic[J].Intelligent Automation and Soft Computing，1996，2(2):103-120.

[13]LIU CAIHUI，MIAO DUOQIAN.Graded rough set model based on two universes and its properties[J].Knowledge-Based Systems，2012，33:65-72.

[14]魏玲.粗糙集与概念格约简理论与方法[M].西安:西安交通大学出版社，2005.

[15]张文修，仇国芳.基于粗糙集的不确定性决策[M].北京:清华大学出版社，2005.