Bootstrap法在机电引信解除保险距离试验中的应用

刘 刚，王 侠，陈 众，赵 新

（中国华阴兵器试验中心，陕西 华阴 714200）

正系数。

将N 个W1 样本w11，w12，w13，…，w1 N 及W2 样本w21，w22，w23，…，w2 N 分别 按照从小到大的 顺 序进行排序，得到整理后的样本。对于W1，变为w1（1），w1（2），w1（3），…，w1（N），对 于W2，变 为w2（1），w2（2），w2（3），…，w2（N），据此我们可构造出引信解除保险距离上下限分位数的单侧置信区间，引入置信度γ，则：

对于p1 分位数，定义：

0 引言

引信解除保险距离试验涉及引信安全性，历来受到靶场的高度重视。近些年来，引信解除保险后立即起爆的试验方法在实践中应用较多，具体实施程序是对引信进行改装后对空射击，一旦解除保险，立即起爆。采用光学经纬仪测量炸点坐标，结合炮位坐标，可直接解算出引信解除保险距离。该方法在诸多引信定型试验中得到成功应用，其优点在于试验简便，可控性强。

假设引信解除保险距离总体为正态分布N（μ，σ2），记xp1为总体p1分位数，称为下限分位数，xp2为总体p2分位数，称为上限分位数，实际中一般取p1=0.05，p2=0.95。在引信解除保险后立即起爆试验中，若干发引信可视为从总体中随机抽取的样本，我们的任务是利用样本数据估计总体的上下限分位数。现行数据处理方法为计算样本均值和标准差，以样本均值和标准差代替总体均值和标准差，从而直接计算得到总体上下限分位数。这种方法简单易行，但显而易见，样本均值和标准差可能无法准确反映总体均值和标准差，从而在计算上下限分位数时出现较大散布，造成试验误判。

Bootstrap法在武器系统试验数据处理方面已得到大量应用，但在引信解除保险距离试验领域尚未见报道。为解决现行方法存在的问题，本文提出了基于Bootstrap法的机电引信解除保险距离试验数据处理方法。

1 现行方法原理及仿真计算

1.1 现行方法原理

引信解除保险距离X 可视为一随机变量，服从正态分布（根据以往经验，引信解除保险后立即起爆试验数据均能通过正态性分布检验），即X～N（μ，σ2），根据统计原理［1］有：

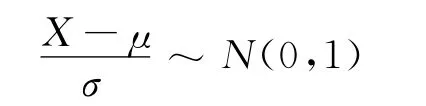
因此，N（μ，σ2）的ρ分位数xρ是以下方程的解

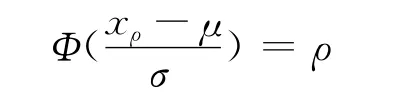
式中Φ（·）为标准正态分布函数，进一步得：

式中μρ为标准正态分布的ρ 分位数，进一步得：

设引信解除保险即起爆试验中获得的样本序列为x1，x2，x3，…，xn，那么μ 的估计为：

σ的估计为：

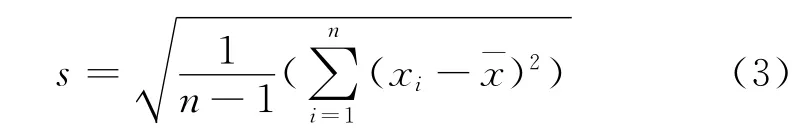
将式（2）、式（3）代入式（1），可得：

式（4）即为n个样本条件下正态分布总体的p分位数估计公式。

1.2 现行方法仿真计算

仿真计算的一般流程为：

1）假设总体分布已知，即正态分布N（μ，σ2）的两个参数μ、σ已知；

2）在N（μ，σ2）下生成3 000组随机样本，样本量为n；

3）计算每组样本的样本均值和标准差；

4）按式（4）计算每组样本的总体上下限分位数。

令μ=120，σ=10，n=10，下限分位数取x0.05，下限分位数取x0.95。编制仿真程序，计算结果如表1。同时给出其中一次仿真计算结果，见表2。

从表1中可看出，平均来说，现行方法对于总体参数μ、σ、x0.05、x0.95的估计结果是较理想的，然而，这一结论只在“平均意义”成立，由于抽样的随机性，造成^x0.05、^x0.95有较大的散布，单次样本下^x0.05与x0.05真值之间的差值在（-18.37，15.38）间变化；^x0.95与x0.95真值之间的差值在（-15.55，17.67）间变化，而试验只对单次抽样负责，这意味着单次试验散布较大，可能存在比较严重的估计偏差。

表1 现行方法仿真结果

表2 现行方法单次仿真结果Tab.2 Single Simulation recsult

对于x0.05，术语可表达为引信在距炮口103.55m以内解除保险的概率为0.05，但在单次试验中，计算结果可能表达为引信在距炮口103.55+15.38=118.93m 以内解除保险的概率为0.05，人为地把引信保险距离扩大了15.38 m；对于x0.95，可表达为引信在距炮口136.44m 以外解除保险的概率为0.95，同样在单次试验中，计算结果可能表达为引信在距炮口136.44-15.55=120.89m以外解除保险的概率为0.95，人为地把引信可靠解除保险距离减小了15.55m。

1.3 对判定引信解除保险距离上下限的讨论

对于引信解除保险距离下限，意味着在此距离以内，引信解除保险的可能性较低，估计值应尽量避免冒进，我们关心的是估计值的置信下限，这样才能有把握为部队使用提供更多的安全余量；对于引信解除保险距离上限，意味着在此距离以外，引信解除保险的可能性较高，我们关心的是估计值的置信上限，这样才能有把握保证引信完全解除保险，进而不影响战术使用。

以上述讨论内容为出发点，根据所谓新单侧容限系数法［2］，将总体p1、p2分位数分别视为一随机变量，表达式分别为：

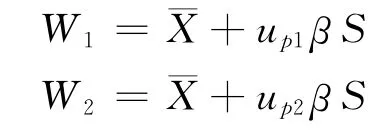
正系数。

将N 个W1样本w11，w12，w13，…，w1N及W2样本w21，w22，w23，…，w2N分别 按照从小到大的 顺 序进行排序，得到整理后的样本。对于W1，变为w1（1），w1（2），w1（3），…，w1（N），对 于W2，变 为w2（1），w2（2），w2（3），…，w2（N），据此我们可构造出引信解除保险距离上下限分位数的单侧置信区间，引入置信度γ，则：

对于p1分位数，定义：

式（5）称为在置信度γ下，引信解除保险距离p1分位数的置信下限。

对于p2分位数，定义：

式（6）称为在置信度γ下，引信解除保险距离p2分位数的置信上限。

2 Bootstrap法在引信解除保险距离上下限估计中的应用

2.1 Bootstrap法简介

Bootstrap法是斯坦福大学Efron教授提出的一种逼近复杂统计量估计值分布的通用方法，该方法摆脱了传统统计方法对分布假定的限制，只依赖于给定的观测样本，适合于任何分布和任何感兴趣的参数估计。

Bootstrap法的核心工作流程是利用经验分布函数代替总体分布函数［3］，从经验分布函数中随机抽取样本以估计统计量的抽样分布。相当于从样本x1，x2，x3，…，xn中进行有放回再抽样，其中x1，x2，x3，…，xn中每一个xi以等概率出现。其基本步骤为：

1）由样本x1，x2，x3，…，xn构造经验分布Fn。

3）用θ＊=θ＊（X＊，Fn）的分布去逼近θ=θ（X，F）的分布（θ＊的分布称为Bootstrap分布）。

从以上关于Bootstrap 法原理的介绍可看出，Bootstrap法解决的恰恰就是前文中N 个W1样本w11，w12，w13，…，w1N及W2样本w21，w22，w23，…，w2N的构造问题，因此Bootstrap法可用于计算引信解除保险距离p1分位数的置信下限及引信解除保险距离p2分位数的置信上限。

由于以上置信上下限估计方法在概率收敛性方面还存在一些不足，Efron提出了改进，即纠偏百分位法，其思路简述为若出现大部分Bootstrap 估计量^θt=θ（X＊t），t=1，2，3，…，T 小于实际样本统计量，则意味着Bootstrap 模拟低估了实际样本统计量，为纠正这一偏差，置信上下限必须向大值调整；相反，如果大部分Bootstrap 估计量大于实际样本统计量，则意味着Bootstrap 模拟高估了实际样本统计量，为纠正这一偏差，置信上下限必须向小值调整。该纠偏过程由纠偏量d0实现［4-6］。

式（7）中，Φ-1［·］为标准正态分布函数的反函数，I（·）为示性函数，其定义为：

当需计算引信解除保险距离的这p1分位数置信下限时，

这样，上文提到的引信解除保险距离p1分位数的置信下限修正为m1（1-γ+2d0）。

当需计算引信解除保险距离的p2分位数置信上限时，

这样，上文提到的引信解除保险距离p2分位数的置信上限修正为m2（1-γ+2d0）。

2.2 具体实施步骤及仿真计算

Bootstrap法的简要计算流程为：

1）假设正态分布N（μ，σ2）的两个参数μ、σ已知，从总体中随机生成n个样本x1，x2，x3，…，xn，方便起见，与前文例子保持一致，取μ=120，σ=10，n=10；

2）计算以上n个样本的p1分位数估计=+以及p2分位数估计=+，取p1=0.05，p2=0.95；

3）以样本x1，x2，x3，…，xn为基础，进行T（T=1 000）次Bootstrap抽样，获得T 个样本，，，…，，计算每个Bootstrap样本的p1分位数估计=¯x＊+μp1βs＊以及p2分位数估计=+μp2βs＊；

4）按照式（7）分别计算两个纠偏量；

6）考虑到随机性因素，重复1）-4）k 次（本文取k=3 000）。

编制相应仿真程序，计算结果如表3。

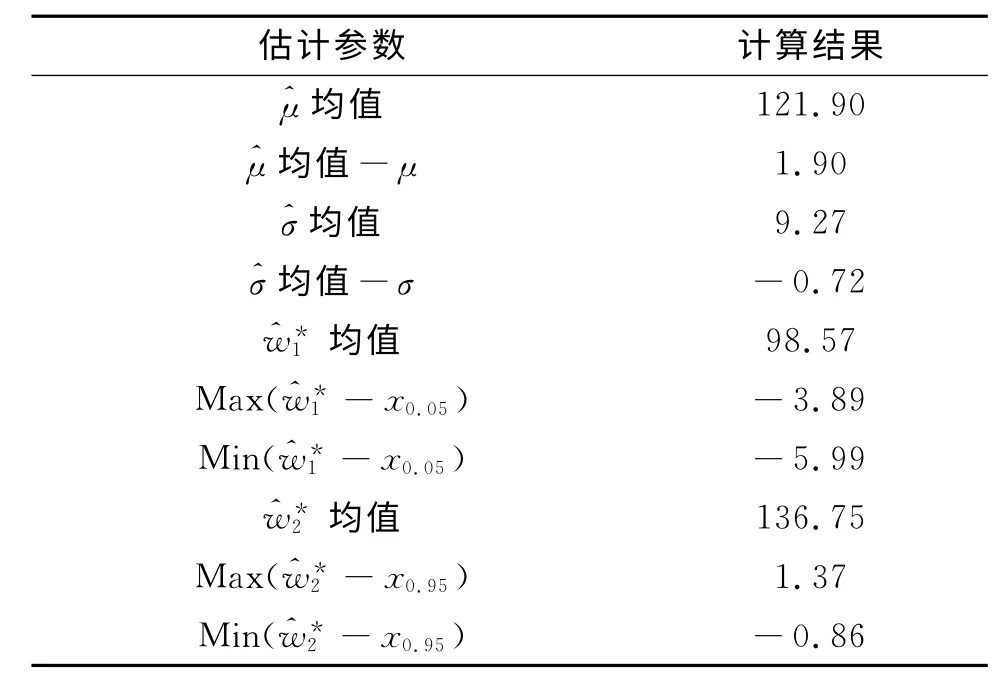
表3 Bootstrap法仿真结果

同时给出其中一次仿真计算结果，见表4。

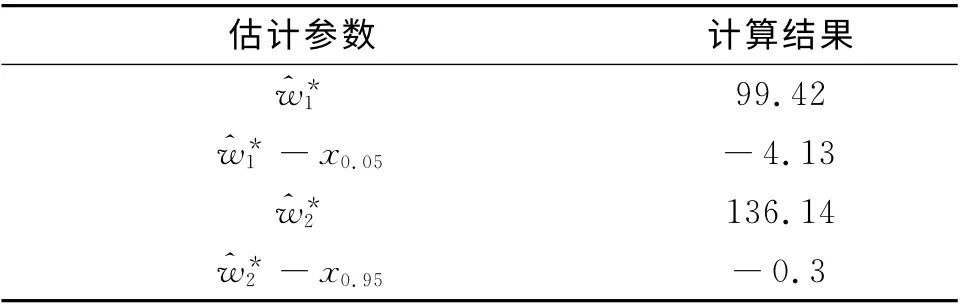
表4 Bootstrap法单次仿真结果Tab.4 Single simulation result of Bootstrap

从表3中可看出，相对于现行方法，Bootstrap法对于总体参数μ、σ、x0.05、x0.95的估计结果均值基本一致，但对于x0.05、x0.95的估计，单次样本下^w＊1与x0.05真值之间的差值在（-5.99，-3.89）间变化；^w＊2与x0.95真值之间的差值在（-0.86，1.37）间变化，最大偏差率由17.7%降低为5.8%，估计结果的单次散布较现行方法大为减小，从而降低了试验误判的可能性。

3 结论

本文提出了基于Bootstrap法的机电引信解除保险距离试验数据处理方法，该方法可有效克服现行方法中单次试验估计偏差大的缺陷。仿真计算结果表明Bootstrap 法上下限分位数单次散布较小，大大降低了试验误判的可能性。

［1］峁诗松.统计手册［M］.北京：科学出版社，2003.

［2］李洪双，吕震宙.小子样场合下估算母体百分位值置信下限和可靠度置信下限的Bootstrap 方法［J］.航空学报，2006，27（5）：789-794.

［3］Wendy L.Martinez.Computational Statistics Handbook with MATLAB［M］.London：Chapman ＆ Hall，2002.

［4］Efron B.The jack knife，the bootstrap，and other resampling plans［M］.Philadelphia：The Society for Industrial and Applied Mathematics，1982.

［5］Efron B.Tibshirani R J.Bootstrap methods for standard errors，confidence intervals，and other measures of statistical accuracy［J］.Statistical Science，1986（1）：54-77.

［6］Efron B.Tibshirani R J.An introduction to the bootstrap［M］.London：Chapman and Hall，1993.