一类常系数非齐次线性微分方程特解的矩阵表示
李 岚
(闽西职业技术学院 基础部,福建 龙岩 364021)
一类常系数非齐次线性微分方程特解的矩阵表示
李 岚
(闽西职业技术学院 基础部,福建 龙岩 364021)
运用微分逆算子移位定理和矩阵运算将一类一阶常系数非齐次线性微分方程的特解用矩阵的形式表示,并在此基础上利用欧拉公式将另一类一阶常系数非齐次线性微分方程的特解也用矩阵的形式表示,用此方法不仅可以简便快捷地计算出这些微分方程的特解,且容易掌握,还可推广到求高阶常系数非齐次线性微分方程的特解.
常微分方程; 特解; 矩阵; 不定积分; 欧拉公式; 算子多项式; 逆算子; 移位定理
n阶复常系数非齐次线性微分方程的一般形式是
y(n)+p1y(n-1)+p2y(n-2)+…+pn-1y′+pny=f(x),
(1)
一阶复常系数非齐次线性微分方程
y′+py=exp(zx)Qn(x),
(2)
y′+py=exp(αx)Qn(x)cosβx,
(3)
y′+py=exp(αx)Qn(x)sinβx,
(4)
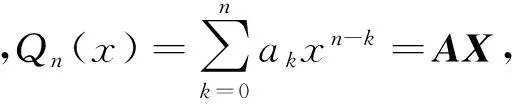
微分方程的特解的求法通常采用:常数变易法、待定系数法、算子解法和拉普拉斯变换法等,各具特色.如待定系数法虽然解题思路简单,易于掌握,但不具有一般性,计算比较繁琐,容易出错.根据微分方程(2)中的自由项的特点可知,该方程的特解仍然是指数函数exp(zt)与一个多项式的乘积,且此多项式的次数与多项式Qn(x)的次数相同或高一次,是n次或(n+1)次多项式,因此求微分方程(2)的特解只需求出此多项式的系数即可.利用参考文献[1]中给出的结论,通过逆算子移位定理和矩阵计算,将微分方程(2)的特解用矩阵的形式表示,并在此基础上利用欧拉公式将微分方程(3)和(4)的特解也用矩阵的形式表示,从而可以根据微分方程的特征根以及自由项的特点选择相应的公式,用矩阵的方法计算出此类微分方程的特解.此方法不仅较为简便,容易掌握,还可以多次重复使用该方法,求出自由项与式(2)、(3)和(4)中的自由项相同的高阶复常系数非齐次线性微分方程的特解.
逆算子移位定理
(5)
引理1[1]不定积分
(6)
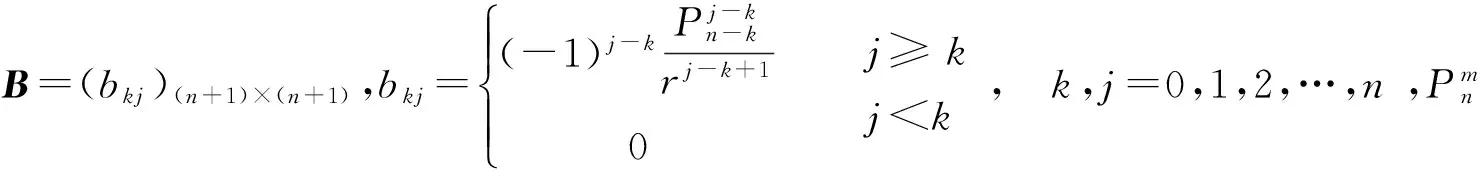
引理2[1]不定积分
(7)

引理3[1]不定积分

(8)
1 主要定理
定理1如果一阶常系数非齐次线性微分方程(2)对应的齐次方程的特征根为r, 则
1)当z≠r时, 微分方程(2)的一个特解为
y*=AB1Xexp(zx),
(9)

j 2)当z=r时, 微分方程(2)的一个特解为 y*=AEXxexp(zx) , (10) 证明1)当z≠r时,根据移位定理和引理1可得 2)当z=r时, 根据移位定理可得 所以结论成立. 定理2如果一阶常系数非齐次线性微分方程(3)对应的齐次方程的特征根为r=α1+iβ1, 则 1)当α+iβ≠r时, 微分方程(3)的一个特解为 y*=exp(αx)/2[A(B2+B3)Xcosβx+iA(B2-B3)Xsinβx], (11) 2)当α+iβ=r时, 微分方程(3)的一个特解为 y*=exp(αx)/2[A(Ex+B4)Xcosβx+iA(Ex-B4)Xsinβx], (12) 1)当α+iβ≠r时 2) 当α+iβ=r时, 所以结论成立. 定理3如果一阶常系数非齐次线性微分方程(4)对应的齐次方程的特征根为r=α1+iβ1, 则 1) 当α+iβ≠r时,微分方程(4)的一个特解为 (13) 2) 当α+iβ=r时, 微分方程(3)的一个特解为 (14) 推论1 如果一阶常系数非齐次线性微分方程(3)对应的齐次方程的特征根为实数r, 则 y*=(AC3Xcosβx+AC4Xsinβx)exp(αx) , (15) 证法一由于 (AC3Xcosβx+AC4Xsinβx)exp(αx) . 所以结论成立. 证法二根据移位定理和引理2 可得 所以结论成立. 推论2 如果一阶常系数非齐次线性微分方程(4)对应的齐次方程的特征根为实数r, 则 y*=(AC3Xsinβx-AC4Xcosβx)exp(αx) . (16) 根据移位定理和引理3,类似推论1即可证明. 由式(9)~(16)可知只须通过简单的矩阵运算即可简便快捷地求出微分方程(2)、(3)和(4)的特解,具体步骤如下: 步骤2根据微分方程(2)中z及对应齐次方程的特征根r求出(n+1)阶方阵矩阵B1=(bkj)(n+1)×(n+1)或E(或根据微分方程(3)和(4)中的α,β及对应齐次方程的特征根r,求出矩阵B2,B3或B4); 步骤3求出矩阵A与矩阵B1的乘积AB1,所求出的一行(n+1)列矩阵,即为微分方程(2)的特解中的多项式的各次项的系数(若是微分方程(3)和(4)则同时求A(B2+B3)和iA(B2-B3),代入式(11)或(12)即可求出该微分方程的特解). 如果是高阶常系数线性微分方程,则可多次重复使用上述步骤求出方程的特解. 当自由项的形式如式(2)的m阶微分方程,可先求出对应齐次方程的m个特征根,再按照定理1,求出这m个特征根对应的(n+1)阶方阵矩阵B11B12…B1m(其中B1k,k=1,2,…,m,表示第k个特征根对应的矩阵),最后将矩阵A与它们全部相乘(即AB11B12…B1m)便可求出m阶微分方程的特解. 当自由项的形式如式(3)和(4)的二阶实常系数线性微分方程,先求出对应齐次方程的2个特征根,再根据推论1、2求出2个特征根对应的(n+1)阶方阵矩阵C31C41C32C42(其中C3k,C4k,k=1,2表示第k个特征根对应的2个矩阵),最后分别求出A(C31C32-C41C42)和A(C31C42-C41C32),便可求出微分方程的特解. 例1求微分方程y′-4y=exp(2x)(x4-3x2-x2+5x-3)的特解. 解微分方程对应的齐次方程的特征根为r=4,由微分方程中的自由项exp(2x)(x4-3x2-x2+5x-3)可知:A=(1 -3 -1 5 -3),z=2,z≠r, 例2求微分方程y′+(-1+i)y=exp(x)(3x2+x-1)sin 2x的特解. 解微分方程对应的齐次方程的特征根为r=1-i,α1=1,β1=-1,由微分方程中的自由项exp(x)(3x2+x-1)sin2x,可知:A=(3 1 -1),α=1,β=2,1+2i≠r, 依据定理3的式(13)可得微分方程的特解为 例3求微分方程y‴-3y″+7y′-5y=exp(x)(4x2+2x-3)的特解. 解微分方程对应的齐次方程的特征根为r1=1+2i,r2=1-2i,r3=1,由微分方程中的自由项exp(x)(4x2+2x-3)可知:A=(4 2 -3),z=1,z=r3, 例4求微分方程y″-y′-2y=exp(2x)(x2+2x-1)cosx的特解. 依据推论1和2的式(15)和(16)可得微分方程的特解为 针对微分方程(2)、(3)和(4),运用逆算子移位定理和矩阵运算推导出求这类微分方程的特解的矩阵计算方法,由于该方法是将微分方程的特征根、自由项中的多项式的系数以及指数式中的次数等数值提取,进行简单的矩阵计算,不仅较为简便,容易掌握,还能为求自由项与此类函数相同的高阶常系数线性微分方程的特解提供解题依据. [1] 李岚.一类函数积分的矩阵表示及其推广[J].海南大学学报(自然科学版),2014,32(1):39-44. [2] 高泽图.关于Euler 数与Stirling 数的几个恒等式[J].海南大学学报(自然科学版), 2002,20(1):12-14. [3] 丁同仁, 李承志.常微分方程教程[M].北京: 高等教育出版社, 1991. [4] 陈纪修,於崇华,金路.数学分析(上、下册)[M].第2版.北京: 高等教育出版社,2004. [5] Hubbard J H, West B H.Differential Equations[M].[S.l.]:Springer-Verlag, 1993. [6] Leon S J.线性代数[M].第8版.张文博,张丽静,译.北京: 机械工业出版社,2010. [7] 阿诺尔德 B N.常微分方程[M]. 沈家骐, 周宝熙, 卢亭鹤,译.北京: 科学出版社, 1985. [8] 方保镕,周继东,李医民.矩阵论[M].北京: 清华大学出版社,2004. [9] Horn R A,Johnson C R.Matrix Analysis[M].Cambridge:Cambridge University Press,1985. [10] 华东师范大学数学系.数学分析(上、下册)[M].第3版.北京: 高等教育出版社,2002. [11] 同济大学教研室.高等数学(上、下册)[M].第4版.北京:高等教育出版社,1996. [12] Lancaster P,Tismenetsky M.The Theory of Matrices[M].2nd ed.[S.l]:Academic Press,Inc,1985. [13] 史荣昌,魏丰.矩阵分析[M].第3版.北京: 北京理工大学出版社,2010. [14] 丘维生.高等代数(上册)[M].北京:高等教育出版社,1996. [15] 王高雄, 周之铭, 朱思铭, 等.常微分方程[M].北京: 高等教育出版社, 2006. [16] 居余马.线性代数[M].第2版.北京: 清华大学出版社,2002. Matrix Representation for a Particular Solution to a Class of Inhomogeneous Linear Differential Equation with Constant Coefficients Li Lan (Department of Basic Courses, Western Fujian Vocational and Technical College, Longyan 364021, China) In the report, the differential inverse operator shift theorem and matrix operation were used to show the particular solution for a class of 1st-order inhomogeneous linear differential equation with constant coefficients in the form of matrix, and on which Euler’s formula was used to show the particular solution for another class of 1st-order inhomogeneous linear differential equation with constant coefficients in the form of matrix. The method, which is easy to master, not only work out the particular solution to such differential equations very easily, but also can be applied to seeking a particular solution to a higher-order homogeneous linear differential equation with constant coefficients. ordinary differential equation; particular solution; matrix; indefinite integral; Euler’s formula; operator polynomial; inverse operator; shift theorem 2015-05-11 李岚(1964- ),男,福建永定人,副教授,研究方向:微分方程,E-mail:1090615490@qq.com 1004-1729(2015)04-0310-08 O 175.1 A DOl:10.15886/j.cnki.hdxbzkb.2015.0055

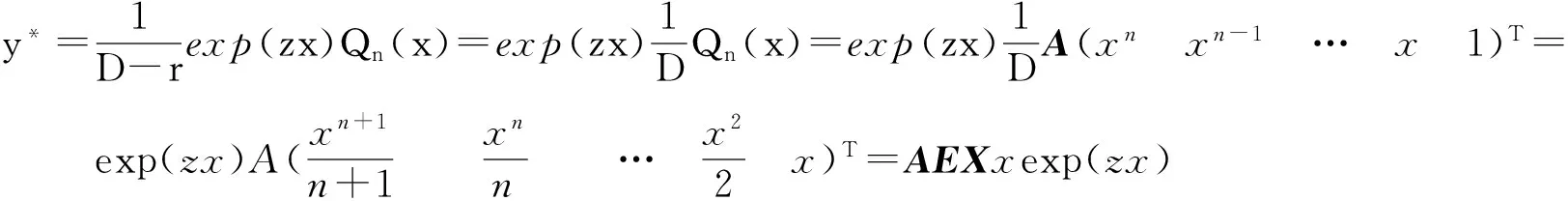



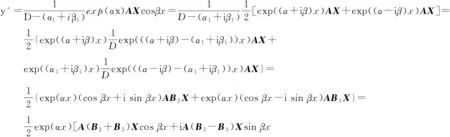

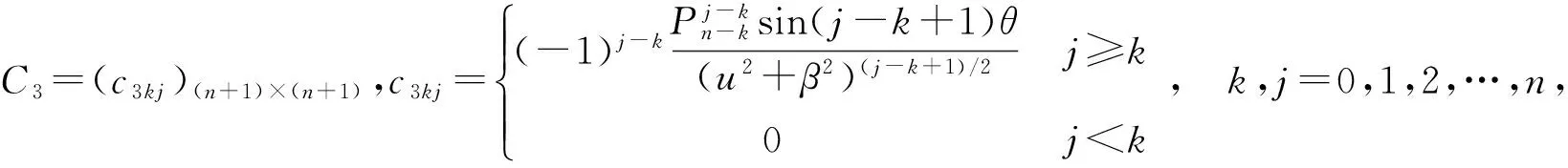

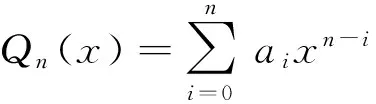
2 应用举例



3 小 结

