Dynamic Response of a Riser Under Excitation of Internal Waves

LOU Min, YU Chenglong, and CHEN Peng



Dynamic Response of a Riser Under Excitation of Internal Waves

LOU Min*, YU Chenglong, and CHEN Peng

,,266580,

In this paper, the dynamic response of a marine riser under excitation of internal waves is studied. With the linear approximation, the governing equation of internal waves is given. Based on the rigid-lid boundary condition assumption, the equation is solved by Thompson-Haskell method. Thus the velocity field of internal waves is obtained by the continuity equation. Combined with the modified Morison formula, using finite element method, the motion equation of riser is solved in time domain with Newmark-β method. The computation programs are compiled to solve the differential equations in time domain. Then we get the numerical results, including riser displacement and transfiguration. It is observed that the internal wave will result in circular shear flow, and the first two modes have a dominant effect on dynamic response of the marine riser. In the high mode, the response diminishes rapidly. In different modes of internal waves, the deformation of riser has different shapes, and the location of maximum displacement shifts. Studies on wave parameters indicate that the wave amplitude plays a considerable role in response displacement of riser, while the wave frequency contributes little. Nevertheless, the internal waves of high wave frequency will lead to a high-frequency oscillation of riser; it possibly gives rise to fatigue crack extension and partial fatigue failure.

dynamic response; marine riser; internal waves

1 Introduction

With increasing decline of petroleum resources, especially onshore resources, oil and gas exploration and development in deepwater have become the hot spot of the world energy industry (Li., 2010). However, in South China Sea the internal waves occur frequently as the seawater is deep and with serious density stratification (Moore and Lien, 2007), and the large amplitude waves are believed to be responsible for a great deal of damage in marine structures (Bole, 1994). Internal waves are buoyancy waves caused by variations in density, propagating at the interface between a layer of warmer water and a layer of cooler water beneath. It can propagate in a number of ways, including short regular waves, cnoidal and solitary waves, wave rays and internal tides (Walker, 1998). So far, a considerable number of accidents caused by internal waves have been reported. Osborne and Burch (1980) mentioned that an oil rig located at the Andaman Sea was displaced 30.48m and swung 90˚ for being subjected to strong internal waves; they have been also reported to displace oil platforms as much as 200m in the horizontal direction and 10m in the vertical direction (Chakrabarti, 2005). It follows that the internal wave should be considered in the ocean structure analysis and design.

The research concerning the effects of internal waves on offshore structures is not much available in recent years. Cai. (2003) first introduced Morison empirical formula to estimate the force and torque exerted by internal solitons on cylindrical piles. Ye and Shen (2005) calculated and analyzed the force of internal waves on small- scale cylinder in different frequencies and then compared with that of surface waves and currents. Du.(2007) found that the maximum total force caused by a soliton of a current with a speed of 2.1ms−1is nearly equal to that by a surface wave with a wave length of 300m and a wave height of 18m. A lot of studies have been conducted on the effects of internal solitons on marine risers in time domain by experimental, numerical and even CFD methods (Song, 2011; Chen, 2011; Liu, 2011). Jiang(2012) estimated the dynamic characteristics of a top tension riser (TTR) under internal solitary and non-uniform current by mKDV theory in a two-layer fluid. Guo(2013) computed the dimensionless displacement and stress of a top tensioned riser (TTR) under combined excitation of internal solitary waves, surface waves and vessel motion in time domain. For all of this, most of these studies are concentrated on the internal solitons or internal solitary waves, but few are on the linear internal waves.

This paper aims to explore the effects of linear internal waves on dynamic behavior of a marine riser. The schematic diagram for a top tensioned riser conveying fluid in internal wave field is shown in Fig.1. In Section 2, the differential equation of motion of a marine riser, the governing equation of internal waves and the solution methods are presented, in Section 3 the computational results are discussed, and the conclusions are given in Section 4.

2 Mathematical models and Methods

2.1 Differential Equation of Motion of Riser

The following assumptions are stipulated in the present mathematical models: firstly, the risers are so sufficiently thick-walled that, ideally, their cross-sections remain circular after change of cross-sectional size due to the Poisson’s ratio effect, so that the elastic rod theories are usable, and Brazier effect of flattening of bent tubes is negligible; secondly, longitudinal strain is large, but shear strain is insignificant for elastic rods with high slenderness ratio; thirdly, the internal and external fluids are inviscid, incompressible, and irrotational.

In theplane of Cartesian coordinate system, the horizontal displacement=() in-direction is considered to define the deformation of any points on the neutral axis of the static equilibrium configuration that was obtained from the static analysis. According to mathematical model and strain-displacement relationship, the curvature of the riserand the axial strainare obtained, whereis the arc length of riser element, the superscriptrepresents the derivative of the parameter with respect towith,is the initial axial strain due to the top tension. Then based on the principle of virtual work, the differential equation of motion of a marine riser transporting fluid is (Chucheepsakul., 2003):

where the effective mass per unit length=m+m+m, the subscripts,,standing for the marine riser, the internal flow and the added mass, respectively; the small dot () represents the derivative with respect to time;is the structural damping coefficient;,are the internal flow’s velocity and acceleration, respectively. The effectivetension,hereis the Young’s modulus,is the area of the cross-sec- tion,is the Poisson’s ratio,is the hydrostatic pressure. The additional subscriptsandrefer to the exterior and interior of the riser, the sign function is defined assgn()=0 if<0, else, sgn()=1;is the moment of inertia of the cross-section andFis hydrodynamic force due to the internal waves. Generally,Fis calculated by Morison formula:

, (2)

Herein both ends of the marine riser are assumed to be hinged, and the boundary conditions are by:

2.2 Governing Equation of Internal Waves

In a two-dimensional Cartesian,coordinate system, with the linear approximation, Cai and Gan (1995) gave the second-order differential equation governing the wave function() of internal waves:

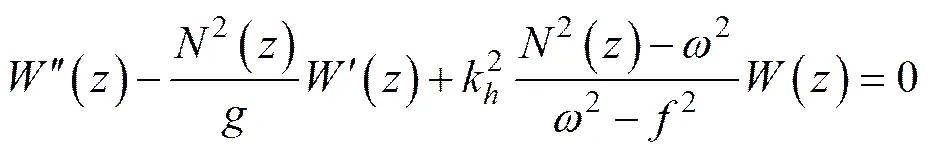
where() is the vertical velocity of internal waves versus depth,is taken vertically upwards,is the gravitational acceleration,kis the horizontal wave number,is the internal wave frequency andis inertial frequency,is the Brunt-Väisälä or buoyancy frequency which is related to the density gradient:

, (5)

in whichis the dimensional density of seawater.

Herein imposing rigid-lid hypothesis at the sea surface, and taking the wall function to model the seabed, then the boundary condition is:

Internal wave dispersion and wave function are determined by Eqs. (4)–(6). Since it is difficult to express() analytically, Cai and Gan introduced the Thompson- Haskell numerical method to solve the governing equation of internal waves.

With the small amplitude wave theory, the vertical velocity of internal waves can be expressed in the form (Ye and Shen, 2005):

where() is the normalized dimensionless amplitude of vertical velocity distributed along the depth in ocean andis the maximum amplitude of vertical velocity.

According to the relation between the vertical displacement of water particlesand vertical velocity, one obtains:

Note that=max, it means that once the maximum wave amplitudemaxis determined, the vertical velocity profile is obtained.

Based on the continuity equation for incompressible flow, the horizontal relative velocityand accelerationof internal waves are obtained with some manipulation:

. (10)

2.3 Solving Method

Discretize Eq. (1) by Hermite interpolation function, obtaining the general form of the finite element method:

where [], [], [] and [] represent the total mass matrix, the total damping matrix, the total stiffness matrix, and the external force matrix, respectively. Eq. (11) is solved directly in time domain with Newmark-method, and the integration constants used are=0.25,=0.5.

3 Numerical Simulations

3.1 Example Data

Consider the dimensional density, which is assumed as in Holmboe model and given by (Ye and Shen, 2005):

where0is the density of seawater in0,0is vertical coordinate of the middle of pycnocline,is half of the thickness of pycnocline,andare dimensionless coefficients correlating with the density. The parameters of seawater model are given in Table 1. Then the density and buoyancy frequency of seawater are obtained as shown in Fig.2.

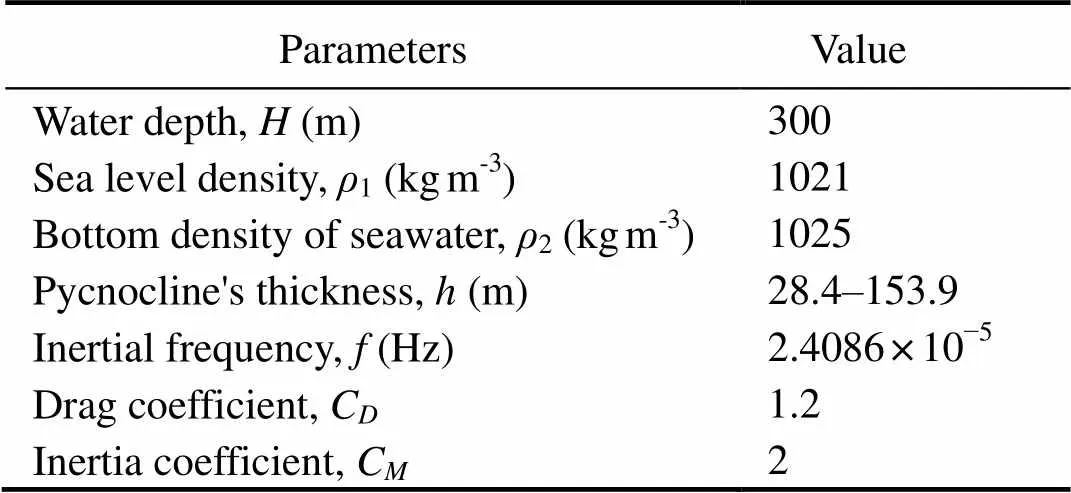
Table 1 Model properties of seawater

Fig.2 Distribution of density ρ and buoyancy frequency N versus depth.

According to vast field observations and investigations of the internal waves in the South China Sea in recent decades (Ebbesmeyer., 1991; Bole., 1994; Qiu., 1996; Fang., 2000; Li., 2003), the internal waves of high frequency (about 3–5cph) and huge amplitude (about 15–100m) are commonly observed. In this study, a typical internal wave with frequency of 5.2358× 10−3rads−1and maximum amplitude of 30m is selected for the calculation.

By solving the governing differential equation of internal wave using the Thompson-Haskell method with a vertical resolution of 1m, the distribution of waves eigenfunction for the first three modes are obtained. The horizontal wave numberkare 0.00378, 0.01553 and 0.02628m−1, respectively. Meanwhile, the wave amplitudes of 2ndand 3rdmodes are assumed as 1/2 and 1/3 that of 1stmode (Ye and Shen, 2005), thus, the horizontal velocity distribution of internal waves versus depth is computed and shown in Fig.3. It is found that the internal waves result in a shear flow in the sea water.

Fig.3 Horizontal velocity amplitude of internal waves corresponding to the first three modes.

The riser parameters and their values employed in the calculation are presented in Table 2. The total water depth is 300m while the riser is 20m above the water surface.

Table 2 Model parameters of marine riser

3.2 Dynamic Responses of Riser under Internal Waves

Program resp.m in MATLAB is developed to solve the dynamic responses in internal wave field, and the data given in Tables 1 and 2 are employed to the compiled code. In addition, the pipe59 element in ANSYS software is used to simulate the movement of riser, the force of internal wave is computed by Morison formula, and finally the prestress method is taken in transient analysis. The results of time history of riser under internal waves and the maximum transfiguration are shown in Figs.4 and 5, respectively. Apparently, the results obtained are in very good agreement.

Fig.4 Time history of riser displacement under internal waves: (a) 1st mode, H=−50m; (b) 2nd mode, H=−100m; (c) 3rd mode, H=−115m.

Fig.5 Maximum deformation of riser: (a) 1st mode; (b) 2nd mode; (c) 3rd mode.

It can be seen from Fig.4 that the oscillating cycles of riser in different modes of internal wave are the same as the wave period. However, Fig.5 displays that the configurations of riser appear in different shape. Meanwhile, the reversal point is located in upper layer in the 1stmode while it shifts downward to the mixing layer in the higher mode. Furthermore, the maximum displacements of riser under the first three modes of internal waves are 0.21, 0.10 and 0.002m, respectively. Apparently, it suggests that the first mode of internal wave plays the dominant role in the dynamic response of marine riser.

3.3 Effect of Wave Amplitude

In order to ascertain the dynamic behavior of marine riser under internal waves with different amplitudes, the variation of wave amplitude is taken to be between 15 and 100m. Fig.6 portrays the effect of wave amplitude on the dynamic response of marine riser in internal wave field. To show the nonlinearity more clearly, we use non- dimensional displacement (displacement divided by wave amplitude, D/A) in this graph. It is found that the wave amplitude has a considerable influence on the dynamic responses of riser. As the wave amplitude increases, the response displacements of riser increase greatly. And the phenomenon is more apparent with high value of wave amplitude.

Fig.7 shows the relation between riser displacement and wave amplitude of internal waves. As witnessed previously, the wave amplitudes quadratically increase the res- ponse displacements.

Fig.6 Time history of riser displacement under internal waves of different amplitudes.

Fig.7 The function relation between riser displacement and internal wave amplitudes.

3.4 Effect of Wave Frequency

To study the effect of wave frequency on the response performance of marine riser in internal wave field, the circular frequency of internal waves is calculated from 1.745×10−3to 1.047×10−2rads−1 in this section. Fig.8 depictsthe time history of maximum displacement of riser under internal waves of different frequencies. In all cases, the response frequencies of riser are always the same as the wave frequencies. From low to high wave frequency, the response displacements of riser are reduced in some degree; this is more apparent with high value of displacement. However, compared with the wave amplitude, the wave frequency has less effect in the response displacement of riser. Nevertheless, the internal waves of high wave frequency will result in a high-frequency oscillation of riser; it possibly gives rise to the fatigue crack extension and the partial fatigue failure, even leakage.

Fig.8 Time history of riser displacement under internal waves of different frequencies.

4 Conclusions

In this paper, the dynamic behavior of a marine riser under excitation of internal waves is presented. Based on the linear approximation, the horizontal velocity fields of internal waves are obtained. Combined with the Morison formula, the differential equation of marine riser motion is solved. We get the riser’s response displacement and transfiguration. The effect of parameters of internal waves is discussed in detail. The following conclusions are drawn:

1) Internal waves of the first two modes play a dominant role in dynamic responses of a marine riser. The response performance of the riser diminishes rapidly with higher modes.

2) The deformations of riser have different shapes under different modes of internal waves. The location of maximum displacement shifts downward.

3) The wave amplitude of internal waves quadratically increases the response displacement of marine riser. It plays a considerable role in response displacement of riser, while the wave frequency contributes little.

Acknowledgements

This research is funded by the Fundamental Research Funds for the Central Universities (No. 11CX04018A) and the National Natural Science Foundation of China (No. 51309241).

Bole, J. B., Ebbesmeyer, J. J., and Romea, R. D., 1994. Soliton currents in South China Sea: Measurements and theoretical modeling.. Houston, Texas, 367-375.

Cai, S. Q., and Gan, Z. J., 1995. A numerical method of internal waves dispersion relation., 14 (1): 22-29 (in Chinese with English abstract).

Cai, S. Q., Long, X. M., and Gan, Z. J., 2003. A method to estimate the forces exerted by internal solitons on cylindrical piles., 30 (5): 673-689.

Chakrabarti, S., 2005.Elsevier Ltd., Vol. 1, 105-106.

Chen, W. M., Zheng, Z. Q., and Zhang, L. W., 2011. Vortex-induced vibration of deepwater flexible riser experiencing internal-wave-induced shear flow., 28 (12): 250-256.

Chucheepsakul, S., Monprapussorn, T., and Huang, T., 2003. Large strain formulations of extensible flexible marine pipes transporting fluid., 17 (2): 185-224.

Du, T., Sun, L., and Zhang, Y. J., 2007. An estimation of internal soliton forces on a pile in the ocean., 6 (2): 101-106.

Ebbesmeyer, C. C., Coomes, C. A., and Hamilton, R. C., 1991. New observation on internal wave (solutions) in the South China Sea using an acoustic Doppler current profiler.. New Orleans, 165-175.

Fang, X. H., Jiang, M. S., and Du, T., 2000. Dispersion relation of internal waves in the western equatorial Pacific Ocean., 19 (4): 37-45.

Guo, H. Y., Zhang, L., and Li, X. M., 2013. Dynamic responses of top tensioned riser under combined excitation of internal solitary wave, surface wave and vessel motion., 12 (1): 6-12.

Jiang, W. J., Lin, Z. Y., and You, Y. X., 2012. Dynamic characteristic of a top tension riser under combined excitation of internal solitary wave and non-uniform current., 27 (4): 424-435 (in Chinese with English abstract).

Li, P. L., Zuo, J. C., and Li, L., 2003. Characteristics of the transition layer in the South China Sea., 21 (1): 27-33 (in Chinese with English abstract).

Li, X. D., Zhao, Z., and Wen, Z. X., 2010. Development trends of world upstream oil and gas industries., 37 (5): 623-627.

Liu, B.T., Li, W., and You, Y. X., 2011. Numerical simulation of interaction of internal solitary waves with deep-sea risers., 29 (4): 1-7.

Moore, S. E., and Lien, R. C., 2007. Pilot whales follow internal solitary waves in the South China Sea., 23 (1): 193-196.

Osborne, A. R., and Burch, T. L., 1980. Internal solitons in the Andaman Sea., 208 (4443): 451-60.

Qiu, Z., Xu, X. Z., and Long, X. M., 1996. A preliminary analysis on internal tide characteristics at an observation point in Northern South China Sea., 15 (4): 63-67 (in Chinese with English abstract).

Song, Z. J., Teng, B., and Gou, Y., 2011. Comparisons of internal solitary wave and surface wave actions on marine structures and their responses., 33 (2): 120-129.

Walker, S. A., Martin, A. J., and Easson, W. J., 1998. Velocity fields in solitary internal waves.. Montreal, Canada, 11-17.

Ye, C. S., and Shen, G. G., 2005. Numerical calculation and analysis about internal wave’s force on small-scale cylinder., 38 (2): 102-108 (in Chinese with English abstract).

(Edited by Xie Jun)

DOI 10.1007/s11802-015-2701-2

ISSN 1672-5182, 2015 14 (6): 982-988

© Ocean University of China, Science Press and Spring-Verlag Berlin Heidelberg 2015

(July 4, 2014; revised September 30, 2014; accepted September 15, 2015)

* Corresponding author. Tel: 0086-532-86981701 E-mail: shidaloumin@163.com