6次单位根时小q Schur代数uq（2，r）的生成元与关系式

高文婷

（同济大学 数学系，上海200092）

1 代数U（n）

设v是不定元，令A＝Z[v，v－1].k是一个包含l′次本原单位根ε的域，其中l′≥3.设l＞1且

特别地，当v取值ε时，k可以看成一个A－模.根据文献[1]，记U（n）是 Q（v）上gln的量子包络代数，生成元是Ei，Fi（1≤i≤n－1）和K±1j（1）≤j≤n）.对于m，t∈N和c∈Z，令

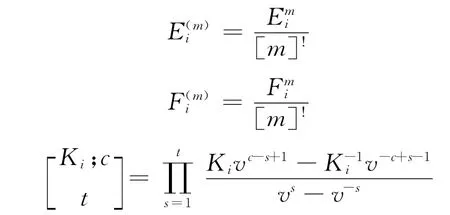
根据文献[2－3]，令UA（n）为由所有Ki生成的U（n）的A－子代数.令Uk（n）＝UA（n）⊗Ak，仍使用相同的符号来记Ei，Fi，Kj在Uk（n）中的像.根据文献[2]，令是由所有Ei，生成的Uk（n）的k－子代数.文献[1]给出了代数的生成元和关系式表现.

2 q－Schur代数

根据文献[4]，令Aq（n）由n2个不定元cij（1≤i，j≤n）生成的k－代数，其中q＝ε2，满足以下关系式：

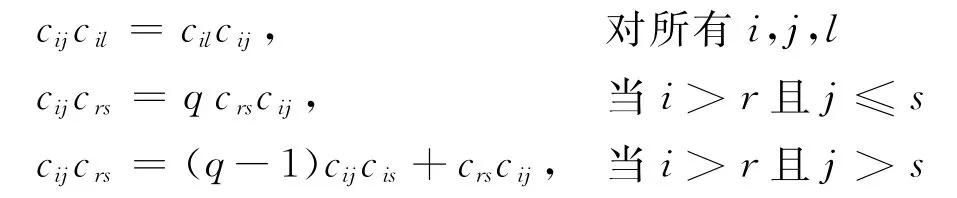
则Aq（n）具有余代数结构

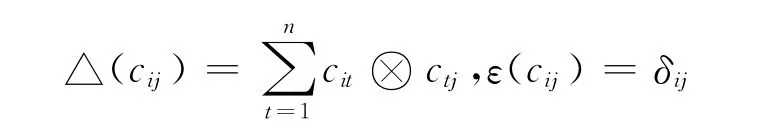
记Aq（n，r）为Aq（n）的r次齐次部分，对所有的r，Aq（n，r）是Aq（n）的子余代数，因此Aq（n，r）＊是k－代数，称为q－Schur代数.

对于A＝（aij）∈Ξ，令

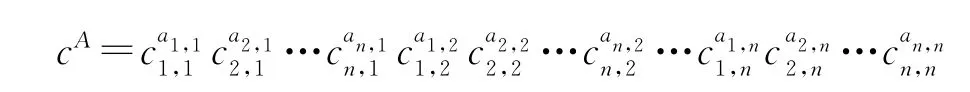
根据文献[4]，集合｛cA｜A∈Ξr｝形成了Aq（n，r）的一组基.若ξA：＝（cA）＊，得到q－Schur代数的一组对偶基｛ξA｜A∈Ξr｝.

令UA（n，r）是文献[5]中定义的A上的代数，它有一组正规A－基｛[A]｝A∈Ξr.记Uk（n，r）＝UA（n，r）⊗Ak，根据文献[4，6]，有

记U（n，r）＝UA（n，r）⊗AQ（v），给定r＞0，A∈Ξ±，j＝（j1，j2，…，jn）∈Zn，定义

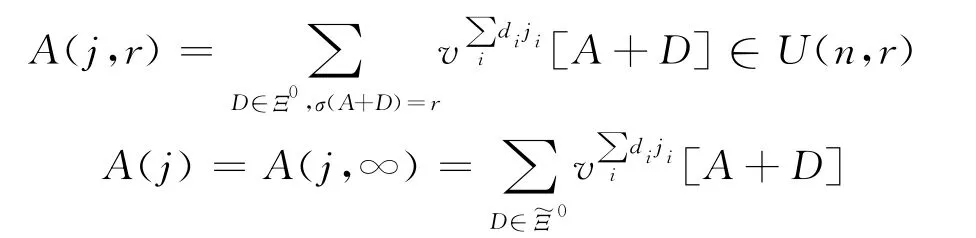
其中Ξ0（或0）为Ξ（或）中的对角矩阵构成的子集合，D是对角矩阵，根据文献[5]有下面的结果.

定理1U（n）与U（n，r）之间有一个代数满同态ζr：U（n）U（n，r），满足

记ei，fi，kj分别是Ei，Fi，Kj在ζr下的像，其中1≤i≤n－1，1≤j≤n.记Λ（n，r）＝｛λ＝（λ1，λ2，…，r）＝｛λ∈Λ（n，r）｜λ1≥λ2≥…≥λn｝.对于t＝（t1，t2，…，tn）∈Nn，令

3 小q－Schur代数uq（n，r）

在文献[6]中已经证明ζr（UA（n））＝UA（n，r），因此ζr诱导了一个满同态：

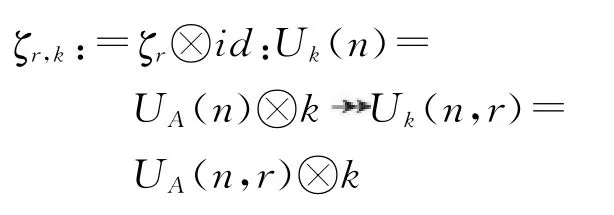
令hi＝（0，…，0，1i，0，…，0）∈Zn，αi＝hi－hi＋1.根据文献[7]，有如下结论.

（1）若存在μ∈Λ（n，r）使得且μi＋1≥1，则；否则

（2）若存在μ∈Λ（n，r）使得且μi≥1，则

4 主要结果

以下假定n＝2，l′＝6，从而，研究6次单位根时小q－Schur代数uq（2，r）的生成元与关系式，有如下结果：

命题2（1）r≥1且r≠5，6，7，8时，uq（2，r）由e，f和生成，其中，并且满足如下关系：

把由命题2（1）（或者命题2（2））中的生成元与关系式定义的代数记作s′.令s′＋，s′－，s′0分别是由在s′中生成的子代数.根据关系①～④（或者⑤～ ⑧），s′＝s′＋s′0s′－.s′可 由

4.1 r＝1，2，3，4

引理1r分别取值1，2，3，4时，集合M′：＝，其中μ∈Λ（2，r），满足均张成s′.

证明 首先，根据关系①～④，s′由张成，其中其 次，对 于，其中μ∈Λ（2，r），满足｝中的

元素，均可由M′中的元素表示.

（1）对于r＝1，根据关系②，a，b∈｛0，1｝.

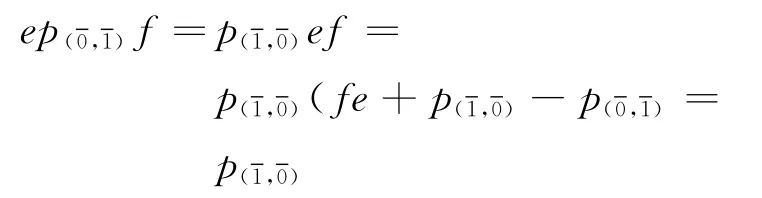
因此结论成立.

（2）对于r＝2，根据关系②，a，b∈｛0，1，2｝.

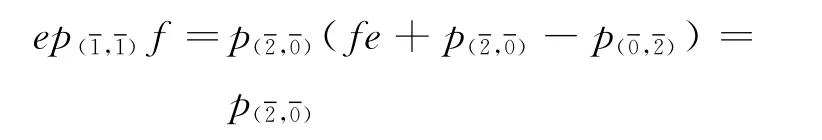
余下的由关系④知结论成立.

（3）对于r＝3，根据关系②，a，b∈｛0，1，2｝.

因此结论成立.

（4）对于r＝4，根据关系②，a，b∈｛0，1，2｝.

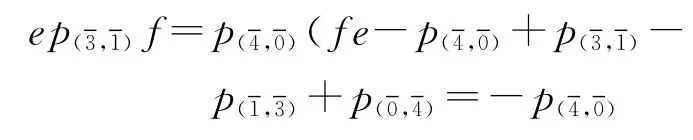
因此结论成立.

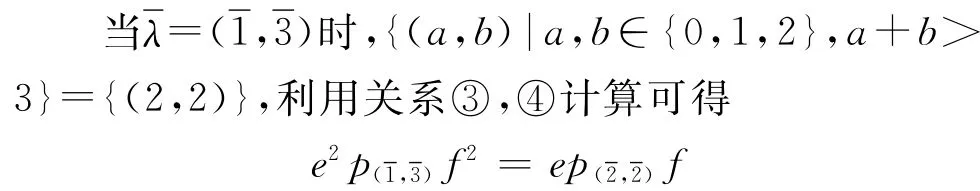
因此结论成立.

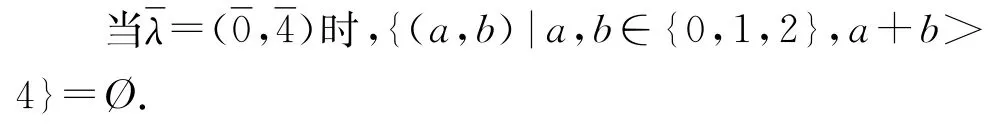
命题4r分别取值1，2，3，4时，均有代数之间的同构s′≌uq（2，r）满足并且M′是uq（2，r）的一组基.

证明 当r分别取值1，2，3，4时，在uq（2，r）中，关系①～④成立.从而得到代数满同态η：s′→uq（2，r）满足η（e）＝e，η（f）＝f，.根据文献[1]，当r分别取值1，2，3，4时，经计算可分别得到dimuq（2，r）等于4，10，18，27；而相应地，＃M′分别等于4，10，18，27，因此命题得证.

4.2 r＝5，6，7，8

引理2r分别取值5，6，7，8时，集合M′：＝，其中μ∈Λ（2，r），满足张成s′.

证明 首先，根据关系⑤～⑧，s′由张成，其中a，b∈ ｛0，1，2｝，.其次，对于，其中μ∈Λ（2，r），满足中的元素，均可由M′中的元素表示.

（1）对于r＝5

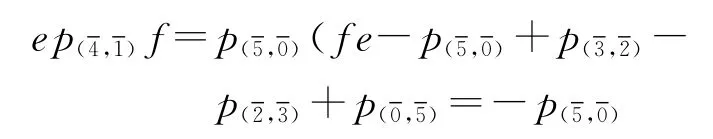
余下的由关系⑧知，结论成立.

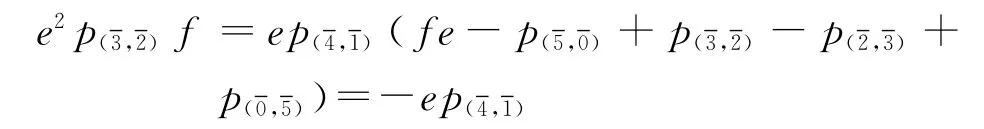
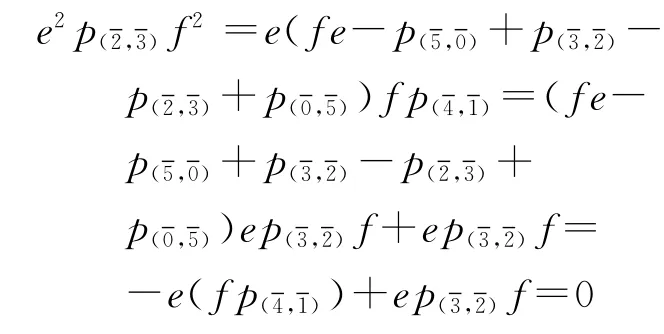
因此结论成立.

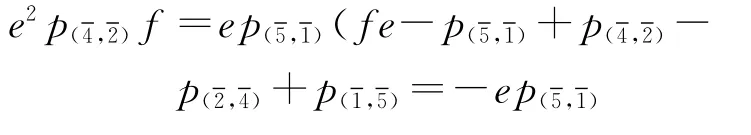
（4）对于r＝8

命题5r分别取值5，6，7，8时，均有代数之间的同构s′≌uq（2，r）满足并且M′是uq（2，r）的一组基.

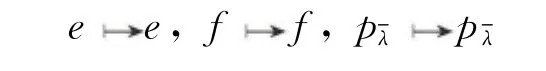
证明 在uq（2，r）中，关系⑤～⑧成立.

在uq（2，5）中，关系⑨显然成立.

在uq（2，6）中，有同理可得到，所以关系⑨对于r＝7成立.

从而当r分别取值5，6，7，8时，均有代数满同态η：s′uq（2，r）满足根据文献[1]，当r分别取值5，6，7，8时，经计算可分别得到dimuq（2，r）等于36，44，50，53；而相应地，＃M′分别等于36，44，50，53，因此命题得证.

4.3 r＝9，10，11，12，13，14

根据文献[1]经计算可得到，dimuq（2，9）＝dimuq（2，10）＝ dimuq（2，11）＝dimuq（2，12）＝dimuq（2，13）＝dimuq（2，14）＝54.可知这6个小q－Schur代数的基有一个统一“形式”，其中a，b∈｛0，1，2｝.但是它们的生成元不一样，不难得出它们的生成元与关系式.

4.4 r＞14

根据文献[8]知，取n＝2，l′＝6，则有，当r≥9时，uq（2，r）≌uq（2，r＋6）.再结合文献[8]知，当r＞14时，uq（2，r）的生成元与关系式可以由uq（2，9），uq（2，10），uq（2，11），uq（2，12），uq（2，13），uq（2，14）中得到.

[1] Fu Q.Little q－Schur algebras at even roots of unity[J].Journal of Algebra，2007，311（1）：202.

[2] Lusztig G. Finite－dimensional Hopf algebras arising from quantized universal enveloping algebra[J].Journal of the American Mathematical Society，1990，3：257.

[3] Lusztig G.Canonical bases arising from quantized enveloping algebras[J].Journal of the American Mathematical Society，1990，3（2）：447.

[4] Dipper R，Donkin S.Quantum GLn[C]∥Proceedings of the London Mathematical Society.London：[s.n.]，1991，63：165.

[5] Beilinson A A，Lusztig G，Macpherson R.A geometric setting for the quantum deformation of GLn[J].Duke Mathematical Journal，1990，61（2）：655.

[6] Du J.A note on the quantized Weyl reciprocity at roots of unity[J].Algebra Colloquium，1995，2：363.

[7] Du J，Fu Q，Wang J P.Infnitesimal quantum glnand little q－Schur algebras[J].Journal of Algebra，2005（1）：199.

[8] Du J，Fu Q，Wang J P.Representations of little q－Schur algebras[J].Pacific Journal of Mathematics，2011，257（2）：343.