陶瓷梭式窑的混杂智能控制

朱永红，赵一峰，熊 朦，王 伟

（景德镇陶瓷学院机械电子工程学院，江西 景德镇 333403）

陶瓷梭式窑的混杂智能控制

朱永红，赵一峰，熊 朦，王 伟

（景德镇陶瓷学院机械电子工程学院，江西 景德镇 333403）

针对陶瓷梭式窑控制系统存在系统不稳定，控制方法落后的问题，提出了一种陶瓷梭式窑的混杂智能控制方法。根据陶瓷梭式窑的烧结工艺，利用有限状态机建立了陶瓷梭式窑烧制过程的智能混杂模型。通过专家控制系统，从知识库中获取了一种陶瓷制品的烧成温度曲线。给出了卡尔曼滤波算法,将传统的PID控制方法与卡尔曼滤波方法相结合，设计了基于卡尔曼滤波器的PID混杂智能控制器，较好地实现了对陶瓷梭式窑烧成带温度的智能控制。最后，基于Matlab进行仿真研究，仿真结果表明所设计的控制器是有效和可行的。

陶瓷梭式窑；有限状态机；专家系统；PID混杂智能控制；卡尔曼滤波

0 引 言

在我国，每年都会产出很多各种各样的陶瓷制品，并且出口到其他国家和地区。但是，和一些发达国家相比，在陶瓷生产的过程中，我国陶瓷窑炉生产能耗极大，尤其是在窑炉的结构、燃烧系统、能量的循环利用以及控制系统方面相对落后。因此，国家有关部门把提高窑炉热工效率作为研究开发的关键技术之一。陶瓷梭式窑[1-4]是陶瓷工业应用最广的现代间歇式窑炉之一，广泛应用于卫生洁具、日用陶瓷、艺术瓷和特种陶瓷的烧成，其检测与控制方式直接影响着陶瓷产品质量和能源利用效率。

陶瓷梭式窑是具有大时滞、强非线性、多变量耦合变参数的复杂对象，炉内温度、气氛、压力等受多种因素的影响，其生产过程既受连续时间信号驱动，又受离散事件信号驱动，是个典型的混杂系统。目前，我国陶瓷梭式窑大多采用辅以人工观火的半自动化控制方式，控制方法仍相对比较落后，生产不稳定,工人劳动强度大，严重影响产品质量，所以有必要研究新的控制策略来保证陶瓷梭式窑生产稳定开展。在工业过程控制中常用的控制方法就是 PID 控制[5-6]，传统的PID控制方法在小滞后的情况下效果还可以，但对于本文研究的非线性纯滞后混杂对象而言，采用传统的PID控制就很难达到理想的控制效果。相对于其他的滤波算法而言，卡尔曼滤波算法[8-9]具有很强的差错控制能力，能够将误差控制在很小的范围内，所以本文将卡尔曼滤波方法和PID控制方法结合起来实现对陶瓷梭式窑烧成带温度混杂智能控制。 到目前为止，将这种控制方法应用于陶瓷梭式窑炉温度控制的研究尚未见诸报道。基于以上情况，本文提出了基于卡尔曼滤波器的PID混杂智能控制方法，并对其进行了仿真研究，结果表明所提出的方法是可行和有效的。

通信联系人：朱永红(1965-)，男，博士，教授。

Correspondent author:ZHU Yonghong(1965-), male, Dc., Professor.

E-mail:zyh_patrick@163.com

1 烧制过程模型的建立

1.1 陶瓷梭式窑烧制工艺

陶瓷梭式窑对烧成制品的适应性很强，其炉内温度受多种因素的影响，而烧成制品的质量大多由烧成的工序决定，这就与制品的烧成工艺温度有很大关系。 其主要的烧制过程包括：低温阶段、氧化及还原期、高温阶段和冷却阶段。具体的烧制工艺过程如下：

⑴低温阶段：该阶段一般在400 ℃以前，其升温的速度主要取决于坯体的厚度以及坯体进窑前的含水率，此阶段主要是去除坯体中的水分，若升温太快，可能会导致坯体内部水蒸气压力过大，从而使得坯体开裂。

⑵氧化及还原期：这个温度段一般在900 ℃之前，其升温速度主要取决于泥土的混合比例，火焰性质以及气流的速度。该阶段为成瓷阶段，可以开始加大供气量以及送氧量，窑内温度迅速增加。

⑶高温阶段：这一阶段的最终温度取决于陶瓷的种类，其升温速度取决于窑内的结构以及装窑密度。窑体较大时，升温过快会导致窑内的温差较大，从而导致坯体的收缩成度不一，坯体变形。

⑷冷却阶段：冷却阶段停火进行急冷和缓冷抽风使温度逐渐降低得到陶瓷产品。

1.2 烧制温度曲线的获取

专家控制系统是一种智能计算机程序，它的内部包含了一些领域的专家给出的专门知识和实际经验，能够解决专门的问题。一个具体的专家系统主要包括知识库、推理机、工作数据库、解释机、知识获取机以及用户界面。它们之间的关系如图1所示。

本文针对陶瓷梭式窑烧制温度设计的专家控制系统知识库中包含了卫生洁具、日用陶瓷、艺术瓷和特种陶瓷等各种陶瓷的烧制温度曲线，存储着该领域中所需的专门知识及数据，它是专家系统的组成基础。该专家系统知识库一些数据是从陶瓷窑炉专家在长期的工作过程中所获得的实践经验提炼获取的。专家系统的知识库主要包括理论知识和实践经验。工作数据库是用于存储该领域的初始数据和推理过程中产生的数据。推理机用于记忆所采用的规则，使得整个专家系统可以协调的工作。解释机是用来为用户解释专家系统的行为。

图1 专家控制系统Fig.1 Expert control system

由于受陶瓷种类、大小、泥土混合比例、坯体厚度、坯体含水量以及窑内结构的影响，陶瓷烧制曲线不尽相同。所以由这些不同因素构成了各种各样的陶瓷制品，根据专家经验，将它们不同的烧制曲线存储在知识库中，对某一特定的艺术瓷烧制，利用专家控制系统可得到较为准确的温度烧制曲线。利用专家控制系统得到某种陶瓷产品的温度烧制曲线如图2所示。该温度烧制曲线将作为陶瓷梭式窑控制系统的温度参考输入。

1.3 有限状态机建模

有限状态机是指系统中存在有限个状态，当事件发生时，这些有限个状态进行转移和动作的数学模型。因而，状态的变化是由事件驱动，该事件可以是外部输入的信号，也可以是系统内部的信号，并且在任一时刻，系统只能处于其中的一个状态。在陶瓷梭式窑中， 温度的上升过程可分为各个阶段的工作状态，而在温度上升的过程中，喷嘴的个数的逐个增加又可视为是外部输入的信号，所以，陶瓷梭式窑的生产过程既受时间信号驱动，又受离散事件信号驱动，可以通过有限状态机将烧制过程进行建模。

图2 烧制温度曲线Fig.2 Firing temperature curve

一个完整的有限状态机的设计，应该包括3元素的设计：状态，事件，动作。状态是一种模式，它用于描述事件驱动的系统，其基于事件和条件而改变，处在活动和非活动态之间。事件是动作产生的对象，系统在接收到事件时，就会产生对应的动作。动作是状态间转换的一部分，它是基于状态的活动情况执行，并指示状态的变化。

在有限状态机中，可以通过一种状态转换到另一种状态的条件，并对可转换的状态提供状态迁移事件，从而构造出状态迁移图。在stateflow[7]中，状态和状态转换是最基本的元素，有限状态机的示意图如图3所示，图3中C表示Condition。

针对以上陶瓷梭式窑烧制过程的特征，采用有限状态机进行建模。系统大致分为两个状态，即梭式窑的工作状态和停止状态。工作状态作为三个不同温度状态(High，Middle，Low)的父状态，Low表示低温阶段，Middle表示氧化还原期，High表示高温期。利用Stateflow建模如图4所示。

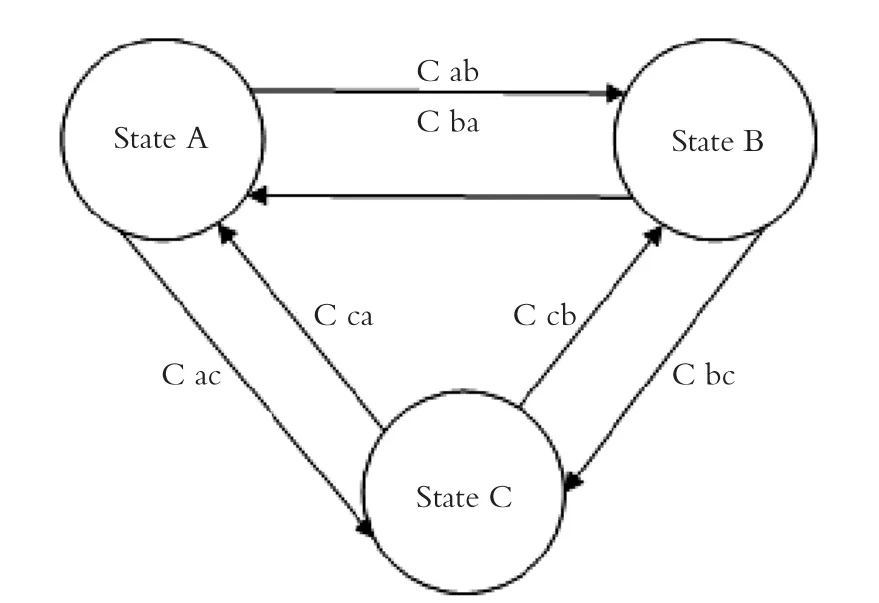
图3 有限状态机示意图Fig.3 Schematic diagram of finite state machine

图4 Stateflow模型Fig.4 Stateflow model

图4为某种陶瓷梭式窑烧制过程Stateflow模型。当梭式窑处于工作状态时，首先是四个喷嘴开始工作，即窑温处于低温阶段；当温度达到800℃时，另两个喷嘴开始工作，此时共有六个喷嘴同时工作，即窑温处于氧化还原期；当温度达到940℃时，最后两个喷嘴开始工作，此时共有8个喷嘴同时工作，即窑温进入高温期。

2 控制器的设计

2.1 数字PID控制

PID模拟控制器控制规律为：

式中，比例环节作用是加快系统的响应速度，当系统产生偏差时，在控制器的作用下，来减小误差。积分环节的作用是消除系统的稳态误差。微分环节的作用是改善系统的动态特性，加快系统的动作速度，减少调节时间。

在计算机控制系统中，必须将模拟PID控制器进行离散化得到数字PID控制器。对式(1)用采样时刻点kT代替连续时间t，用矩形法数值积分近似代替积分，用一阶向后差分近似代替微分，即：

将式(2) 代入式(1) 得到数字PID的位置控制算法为：

2.2 基于卡尔曼滤波器的PID混杂智能控制

在考虑过程噪声和测量噪声作用的情况下，线性离散系统的一般模型为：

式中，x ( k ) 是k时刻的被估计状态变量；yv( k ) 是观测变量；A ( k )是状态转移矩阵；B ( k ) 是噪声输入矩阵；C (k )是测量矩阵；w ( k ) 是过程噪声信号和 v ( k ) 是测量噪声信号。

针对以上模型，卡尔曼滤波器的递推公式为如下式(5)—式(9)：

估计协方差：

滤波器增益：

均方误差矩阵：

状态变量的最优估计值：

其中：Q ( k ) 表示观测噪声协方差，R ( k ) 表示测量噪声协方差，I 表示单位矩阵。

基于式(5)—式(9)，得到如下卡尔曼滤波器算法：

⑴ 计算初始状态x (0)

⑵ 计算 p ( 1 ) 和Mn(1)此时 p ( 1 ) = A ( 1 ) P ( 0 ) AT( 1 ) + B ( 1 ) Q ( 0 ) BT( 1 ) ， M(1)= P(1)CT(1)[C(1)p(1)CT(1)+ R(1)]−1n

⑶ 计算最优估计值

⑷ 计算均方误差矩阵P (1)

根据已知的 p ( 0 ) 和 Mn( 1 ) ，再根据P(1)= [I−Mn(1)C(1)]p(1)求得P(1)。

⑹ 最后利用 ye( k ) =求出每一时刻的输出值。

图5 基于卡尔曼滤波器的PID控制系统结构Fig. 5 PID control system structure based on Kalman filter

基于卡尔曼滤波器的陶瓷梭式窑PID控制系统结构如图5所示。通过前面设计的专家控制系统得到该系统的温度参考输入r，将数字PID控制器和卡尔曼滤波器结合实现对图5中陶瓷梭式窑的烧制温度控制。

3 仿真研究

陶瓷梭式窑是具有大时滞、强非线性、多变量耦合、变参数的复杂对象，其参考模型为：

采用Z变换将以上对象模型进行近似线性离散化，于是得到考虑过程噪声时陶瓷梭式窑控制系统离散状态空间方程为：

带有测量噪声的被控对象输出为：

控制干扰信号 和测量噪声信号 幅值均为0.002的白噪声信号。取w的协方差 ，取v的协方差 。

利用MATLAB软件进行仿真研究，得到基于PID控制的陶瓷梭式窑烧制温度曲线如图6所示。

从图6中可以看出，系统存在较大的超调，且调节时间较长。为了减少超调量，改善烧制温度控制效果，将卡尔曼滤波方法与PID控制方法结合起来用于陶瓷梭式窑烧制温度的控制。基于MATLAB仿真得到基于卡尔曼滤波器的PID控制陶瓷梭式窑烧结温度曲线如图7所示。图7中的虚线为基于卡尔曼滤波器的PID控制获得的烧制温度响应曲线。从仿真图中可以看出，系统不再有超调，并且调节时间缩短，具有较好的鲁棒性。仿真结果表明基于卡尔曼滤波器的PID控制比单纯的PID控制效果更好。

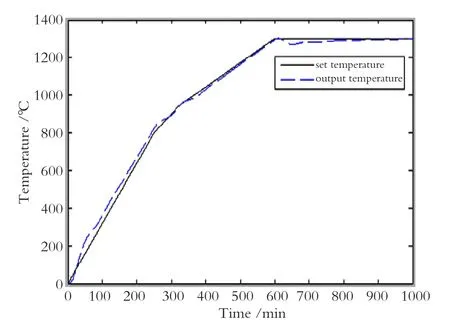
图6 PID控制烧制温度响应曲线Fig.6 Firing temperature response curve based on PID control

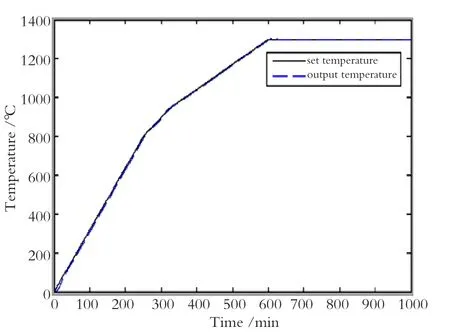
图7 带有卡尔曼滤波器的PID控制烧制温度响应曲线Fig.7 Firing temperature response curve based on PID control with Kalman filter

4 结 论

通过利用有限状态机对陶瓷梭式窑烧制过程进行建模，并利用专家控制系统得到陶瓷梭式窑的温度烧制曲线。将专家控制系统与基于卡尔曼滤波器的PID控制相结合，提出了基于卡尔曼滤波器陶瓷梭式窑混杂PID控制方法，同时给出了卡尔曼滤波算法。最后，针对陶瓷梭式窑模型，并利用基于卡尔曼滤波器的PID混杂控制方法对陶瓷梭式窑烧成带温度控制进行仿真研究，结果表明基于卡尔曼滤波器的PID混杂控制方法比单纯PID控制方法控制效果更好。这一控制方法将为陶瓷梭式窑过程有效控制提供理论依据并具有重要的应用价值，为陶瓷梭式窑温度智能控制提供一种新途径和新方法。

[1] SAIDUR R, HOSSAIN M S, ISLAM M R, et al. A review on kiln system modeling [J]. Renewable and Sustainable Energy Reviews, 2011, 15: 2487-2500.

[2] 江毅. 基于模糊神经网络的梭式窑自适应控制系统应用研究[J]. 机械设计与制造, 2011, 09(09): 60－62.

JIANG Yi. Mechanical Design and Manufacturing, 2011, 09(09): 60-62.

[3] 黎洪生, 苗青, 周瑞敏. 陶瓷窑炉温度控制系统控制算法研究[J]. 武汉理工大学学报, 2014, 36(10): 135-139.

LI Hongsheng, et al. Journal of Wuhan University of Technology, 2014, 36(10): 135-139.

[4] DINH N Q, AFZULPURKAR N V. Neuro-fuzzy MIMO nonlinear control for ceramic roller kiln [J]. Simulation Modelling Practice and Theory, 2007, 15: 1239-1258

[5] WU Ying, JIANG Hang, ZOU Min. The research on fuzzy PID control of the permanent magnet linear synchronous motor [J]. Physics Procedia, 2012, 24: 1311-1318.

[6] SHI Dequan, GAO Guili, GAO Zhiwei, et al. Application of expert fuzzy PID method for temperature control of heating furnace [J]. Procedia Engineering , 2012, 29: 257-261.

[7] 侯世旺, 朱慧明, 李瑞琴, 等. 制造过程不确定质量异常诊断的Stateflow方法[J]. 系统工程理论与实践, 2013, 33(3): 733-740.

HOU Shiwang, et al. System Engineering Theory and Practice, 2013, 33(3): 733-740.

[8] EVENSEN G. The Ensemble Kalman Filter: theoretical formulationand practical implementation [J]. Ocean Dynamics, 2003, 53: 343-367.

[9] 杜航原, 郝燕玲, 赵玉新. 基于模糊自适应卡尔曼滤波的SLAM算法[J]. 华中科技大学学报(自然科学版), 2012, 40(1): 58-62.

DU Hangyuan, et al. Journal of Huazhong University of Science and Technology (Natural science edition), 2012, 40(1): 58-62.

Hybrid Intelligent Control of Ceramic Shuttle Kiln

ZHU Yonghong, ZHAO Yifeng, XIONG Meng, WANG Wei
(School of Mechanical & Electronic Engineering, Jingdezhen Ceramic Institute, Jingdezhen 333403, Jiangxi, China)

To solve the instable and backward control of ceramic shuttle kiln, a hybrid intelligent control method for ceramic shuttle kiln is proposed. A hybrid intelligent model for the sintering process of ceramic shuttle kiln is also established. Sintering temperature curve of a kind of ceramic products is obtained from the knowledge base of expert control system. In the meantime, Kalman filtering algorithm is given. Kalman filter-based PID hybrid intelligent controller is designed by combining traditional PID control method with Kalman filtering method, so as to realize the intelligent temperature control for the sintering zone of ceramic shuttle kiln. MATLAB-based simulation results demonstrate the effectiveness and feasibility of the controller designed.

ceramic shuttle kiln; finite state machine; expert system; PID hybrid intelligent control; Kalman filtering

date: 2015-06-22. Revised date: 2015-07-22.

10.13957/j.cnki.tcxb.2015.06.017

TQ174.6

A

1000-2278(2015)06-0668-05

2015-06-22。

2015-07-22。

国家自然科学基金(61164014，61563022)；江西省自然科学基金(20152ACB20009)；江西省研究生创新基金(YC2014-S316)。