另类“数形结合”帮助学生理解几何证明*——由平行四边形判定教学引发的一点思考

☉广东省广州市景中实验中学 吴颖接

☉广东省广州市第七十八中学 梁 倩

另类“数形结合”帮助学生理解几何证明*
——由平行四边形判定教学引发的一点思考

☉广东省广州市景中实验中学 吴颖接

☉广东省广州市第七十八中学 梁 倩

恩格斯曾说过：“数学是研究现实世界中量的关系与空间形式的科学.”数形结合就是根据数学问题的条件和结论之间的内在联系，既分析其代数意义，又揭示其几何直观，使数量的精确刻画与空间形式的直观形象巧妙、和谐地结合在一起，充分利用这种结合，寻找解题思路，使问题化难为易、化繁为简，从而得到解决.其实按笔者的理解，初中的几何证明就是一个数形结合的好例子.它让学生用文字与符号，对图形进行分析与解释.让学生在思考图形的来龙与去脉的过程中，逐步学会逻辑思考，慢慢学会理性思维.但也因此让许多学生感到十分头痛，易产生畏难情绪.

一、原由

在2014年初二下学期的数学教学中，笔者所任教的初二（1）班的学生学习水平较低.当教到“平行四边形”时，按传统要求，如果证明时要用到初学的定理，必需要写理由.这种做法的原因是：为了加强学生对初学定理的记忆与理解.但几何课上，笔者察觉学生不是心不在焉，就是无精打采，更甚的有一两个在打瞌睡.到了测验时，他们的水平自然是不过关的.这让笔者相当苦恼.笔者试想原因何在？经观察，他们的原因可能有以下几个：（1）不理解；（2）有点理解，但由于定理过多，容易产生混淆；（3）证明的过程太长，再加上要写明理由（注1），嫌烦琐，不想写，久而久之，生疏不会写.面对这一难题，笔者反复思量，结果从全等三角形的几个判定的表述中，得到启发.

全等三角形的几个判定，其表现形式极为简洁，它甚至将判定简化成为字母.如：SSS、SAS、ASA、AAS.这几个定理的简写，给全等三角形的教与学带来很大的帮助.让初学几何的学生，在阅读时更容易得到清晰的形象，而在书写证明表达时，则可以更简便清楚地写出证明的过程.而有些老师甚至会形象地教学生，尖尖的A就是角，而S就是边，以此帮助学生记忆.

二、转化

因为全等三角形的判定具有简洁性、形象性，使绝大部分学生对全等三角形的判定的基础运用是比较容易理解与记忆的.所以笔者认为，四边形边的判定应该也可以进行类似的简化.利用平行四边形的表达符号“▱”，笔者把平行四边形的五个判定方法分别进行了以下的简化：

（1）如图1，两组对边分别平行的四边形是平行四边形.（同向箭头的两直线表示为平行关系）

（2）如图2，两组对边分别相等的四边形是平行四边形.（同向加标注的两直线表示为相等关系）

（3）如图3，一组对边平行且相等的四边形是平行四边形.

（4）如图4，两组对角分别相等的四边形是平行四边形.

（5）如图5，两条对角线互相平分的四边形是平行四边形.

图1

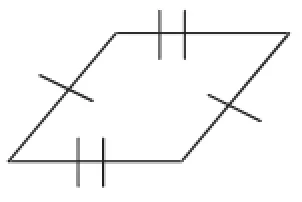
图2

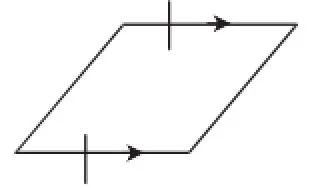
图3

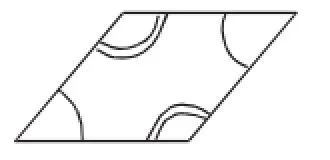
图4

图5

相类似地，特殊平行四边形的判定也可以类似地进行简化.

如矩形的判定：

（1）▱+对角线相等——对角线相等的平行四边形是矩形.

（2）▱+90°——有一个90度角的平行四边形是矩形.

（3）3个90°——有三个90度角的四边形是矩形.

菱形的判定：

（1）▱+邻边相等——一组邻边相等的平行四边形是菱形.

（2）▱+对角线垂直——对角线互相垂直的平行四边形是菱形.

（3）4边等——四条边都相等的四边形是菱形.

这种用简图代替定理的表述文字的做法，笔者给了它一个名称：“以图代理”.

如此，学生在书写相关证明的理由时，可以用这些简图代替相应的文字理由.小小的简图，把长长的文字简略掉了.笔者的学生都感觉很开心，对于平行四边形的很多题目，他们就不再觉得很难了，特别是在初学这些几何定理时，这种做法，对记忆定理和区分这些定理有相当大的帮助.（当然，初学时，还是要求学生看简图，背定理，以巩固和加深理解）

三、应用与反思

不仅学生使用这些图形方便，而且在后面解题时，笔者发现这些简图还有更重要的作用.让我们看一看以下运用简图的证明过程.

图6

例1已知：如图6，AD平分∠BAC，E、F分别为AB、AC上的点且DE∥AC，DF∥AB.求证：四边形AEDF为菱形.

证明：因为DE∥AC，DF∥AB，

又因为AD平分∠BAC，

所以∠EAD＝∠FAD.

因为DE∥AC，

所以∠FAD＝∠EDA，

所以∠EDA＝∠EAD，

所以四边形AEDF是菱形.（▱+邻边相等）

通过上面的例题可以看出，上题中的“以图代理”的做法，既简化了书写，又形象地用图像代替定理的文字表达，帮助了学生理解记忆定理.而实际上这种做法，是将原图中无关的线段省去，并将重要的线段与角抽取出来进行分析，它就完成了一次较完整图形的抽象过程.这使学生明白几何的证明，就是将原图进行分拆，然后抽取出关键的基本图形出来后再重组，并用之对原图进行解释的过程.

另外，根据皮亚杰的儿童认知心理学的理论，儿童认知新事物的能力分为四个阶段，而初中学生的认知水平应属于第三阶段末、或第四阶段（注2）.而新皮亚杰学说则认为，个体是有差异的.在同一年龄段，有些人的认知还在第三阶段，有些人却已在第四阶段了.而且常识告诉我们，在同一班中，学生的认知能力总会有人更强，而有些人则更弱一些.能力较强的学生，能开始脱离具体事物，具有较好的抽象能力，这部分学生的数学能力较强，并不用老师太费心.但相当多的学生的认知能力尚处于认知能力第三阶段末，他们处于具体事物运算阶段，太抽象的东西对他们来讲，是很困难的（注3）.所以如果能以“图”代“理”进行教学，这些简图可以帮助他们对几何图形进行抽象的思考.使他们明白复杂的图形是由几个简单的“基础”图形组成，只要在原图中把这些基础图形找出来，证明的思路就可以相应建立.所以笔者觉得，这种以“图”代“理”的做法，对这一阶段思维能力较弱的学生来理解和巩固几何知识有重大的帮助.

四、效果与拓展

在平行四边形判定的教学中，应用这种以“图”代“理”的方法，笔者所任教初二（1）班的几何成绩有了相当大的提高，在学期的期末考试中，初二（1）班比另一老师教的初二（3）班多了近5分，其中（1）班为81.8，（3）班为77.3.（注4）

在期末考之后，笔者思考到，以“图”代“理”，数形结合的这种方法，不但可以在“平行四边形的判定”中应用，而且在其他的几何内容也可以用到.如初一的“平行线的判定”，到初三“圆”的学习，都可以用到.如平行线与圆的一些重要定理，可尝试作如下表示.

（1）如图7，内错角相等，两直线平行.

（2）如图8，同位角相等，两直线平行.

（3）如图9，同旁内角相等，两直线平行.

（4）如图10，垂径定理.

（5）如图11，圆周角等于同弧所对的圆心角的一半.

（6）如图12，同弧所对的圆周角相等.

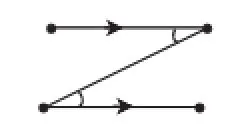
图7

图8

图9

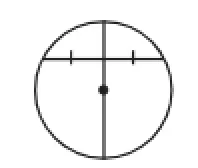
图10

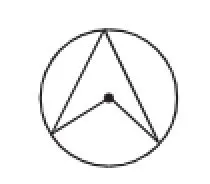
图11

图12

这些简图，在学生初学这些定理时，可以帮助他们更方便地书写证明过程，同时也能更好地记忆定理，更直观地让学生明白，证明几何题实质上是一个分解图形.让他们明白，学几何并不是死背定理.证明应该是一个将复杂的图形拆分为几个基本的图形后，并对之进行解释的过程.这对他们明白几何是怎样建构公理体系的过程，这对学生的逻辑分析能力，都有着很大的帮助.

注1：在中考，几何证明的理由是不用书写的.但在初学一个几何定理时，按传统要求，在初学应用时，要以文字的形式书写几何定理.但学生往往嫌烦琐，不愿写，但矛盾的是，如果不要求学生书写几何理由，学生对定理忘记得很快，遗忘率非常高.

注2：皮亚杰将儿童思维的发展划分为四个大的年龄阶段.这四个阶段分别是：

（1）感知运动阶段（从出生到两岁左右）.这一阶段是思维的萌芽期，是以后发展的基础.皮亚杰认为这一阶段的心理发展决定着未来心理演进的整个过程.

（2）前运算阶段（两岁左右到六七岁）.这一阶段又称前逻辑阶段，这时儿童开始以符号作为中介来描述外部世界，表现在儿童的延缓模仿、想象或游戏之中.

（3）具体运算阶段（六七岁到十一二岁）.在这个阶段，儿童已有了一般的逻辑结构.

（4）形式运算阶段（十一二岁到十四五岁）.此时儿童的智慧发展趋于成熟，思维能力已超出事物的具体内容或感知的事物，思维具有更大灵活性.

注3：根据广州中考数学的相关数据，满分为150分的考试中，每年10万考生，有近1万的考生数学成绩在30分以下.

注4：在初二上学期末，（1）班与（3）班的数学成绩基本相同，相差不到1分.

1.【瑞士】皮亚杰，著.心理发生和科学史［M］.姜志辉，译.上海：华东师范大学出版社，2005.

2.【瑞士】皮亚杰，著.发生认识论原理［M］.北京：商务印书馆，1981.

3.【瑞士】皮亚杰，著.可能性与必然性［M］.熊哲宏，译．上海：华东师范大学出版社，2005.H

*本文系广州市教育科学“十二五”规划（第二批）课题《初中数学有意义学习的课堂教学实践研究》（课题编号12B063）的研究成果之一.