小议复习教学中不等式综合问题探索

筅江苏省徐州第一中学　杜芬

小议复习教学中不等式综合问题探索

筅江苏省徐州第一中学杜芬

函数、数列、不等式考题是高考的传统项目，经久不衰，常考常新，尤其是函数与数列相结合，数列与不等式相结合，函数、数列、不等式三者相结合的题都有一定的难度，综合性较强，但不偏、不怪，思路广、方法多，具有较强的区分层次和选拔功能.从近几年各地试卷压轴题的取材情况来看，归结起来可分为三大类，即函数与不等式型，递推数列与数学归纳法型，以及解析几何型，而且它们明显呈“三足鼎立”的态势.若以数列为载体进行压轴问题的考查，则最后一题都是以点列为载体设制有关数列的问题，重点考查了递推数列、数学归纳法、不等式，它们新颖别致、神奇美妙，而且解题方法独特，别有洞天.高中数学要求的三大能力——思维能力、运算能力和分析解决问题的能力都在这些压轴题的考查中得到了充分的、立体的、集中的体现.这些试题难度较大、综合性强，本文对不等式相关的综合性问题进行分类，引导学生对不同类型的题目进行总结和剖析.

定义：若函数f（x）在x∈I时的值域为开区间（a，b），则称b为f（x）的上确界，a为f（x）的下确界.

恒成立相关性质：

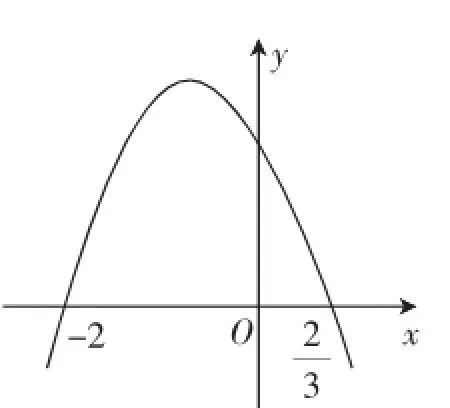
（1）不等式f（x）

（2）不等式f（x）>k在x∈I时恒成立圳f（x）min>k，x∈I，或f（x）的下确界大于或等于k.

存在性相关性质：

（3）不等式f（x）

（4）不等式f（x）>k在x∈I时有解圳f（x）max>k，x∈I，或f（x）的上确界大于k.

一、恒成立问题

不等式综合问题中最常见的是“恒成立”综合试题，通常以函数为载体给出，通过函数的性质、图像等研究函数的最值，不等式在其中主要扮演了“桥梁的作用”，相对于一个变量，两个变量的恒成立成为综合性问题中更需要理解和掌握的.

例1已知两个函数f（x）＝8x2+16x-k，g（x）=2x3+5x2+ 4x，其中k是常数.

（1）对任意x∈［-3，3］，都有f（x）≤g（x）成立，求k的取值范围；

（2）存在x∈［-3，3］，都有f（x）≤g（x）成立，求k的取值范围；

（3）对任意的x1，x2∈［-3，3］，都有f（x1）≤g（x2）成立，求k的取值范围.

解析：（1）设h（x）=g（x）-f（x）=2x3-3x2-12x+k，于是问题就转化为x∈［-3，3］时，h（x）≥0恒成立，故h（x）min≥0.令h′（x）=6x2-6x-12=0，得x=-1或x=2，所以h（x）在［-3，-1］和［2，3］上是增函数，在［-1，2］上是减函数.h（-1）= 7+k，h（2）=-20+k，h（-3）=k-45，h（3）=k-9.h（x）min=k-45，由k-45≥0得k≥45.

（2）由题意知，存在x∈［-3，3］，使得f（x）≤g（x）成立，即h（x）=g（x）-f（x）≥0在［-3，3］内有解，故h（x）max≥0，由（1）知，h（x）max=k+7，于是k≥-7.

（3）本题属于双变量恒成立问题，对任意的x1、x2∈［-3，3］，都有f（x1）≤g（x2）成立，不等式的左右两端函数的自变量不同，x1、x2的取值在［-3，3］上具有任意性，因而使原不等式恒成立的条件是f（x）max≤g（x）min，x∈［-3，3］，f（x）max=f（3）=120-k，g（x）min=g（-3）=-21，即120-k≤-21，解得k≥141.

说明：第（1）（2）问均为单变量恒成立问题，可以利用函数性质或参变分离的方式解决，对于第（3）问，笔者认为双变量恒成立或存在性问题，教师首先要正确加以引导学生的理解，用恰当的类比去理解双变量恒成立是问题解决的关键.

二、存在性问题

图1　

例2设f（x）=ax3+bx2+cx的极小值为-8，其导函数y=f′（x）的图像经过（-2，0）、2两点，如图1所示.

（1）求f（x）的解析式；

（2）若对x∈［-3，3］都有f（x）≥m2-14m恒成立，求实数m的取值范围.

解析：（1）因为f′（x）=3ax2+2bx+c，且y=f′（x）的图像经过（-2，0）、两点，所以，所以f（x）=ax3+2ax2-4ax，由图像可知函数y=f（x）在（-∞，-2）上单调递减，在上单调递增，在2上单调递减，故（fx）=（f-2）=-8，解得a=-1，极小值所以（fx）=-x3-2x2+4x.

（2）要使对x∈［-3，3］都有f（x）≥m2-14m恒成立，只需f（x）min≥m2-14m即可.由（1）可知函数y=f（x）在［-3，-2）上单调递减，在2上单调递增，在3上单调递减，且f（-2）=-8，f（3）=-33-2×32+4×3=-33<-8，所以f（x）min=f（3）=-33，-33≥m2-14m圯3≤m≤11，故所求实数m的取值范围为｛m|3≤m≤11｝.

说明：本题中涉及了导数，试题难度虽然不大，但是运用了数形结合的思想方法，是一道培养能力的好题.我们可以看到以函数为载体，结合不等式相关“桥梁”作用，成为不等式背景下的综合性问题的典型考查方向，这样的试题既是热点也是一个小小的难度.科学方法的掌握立足于平时的学习，在知识的形成、联系和应用中养成科学的态度，平时解题，切忌就题论题，要多方法、多方位、多角度寻求解题途径，在可行方案中求异、求简、求新、求巧.要“借题发挥”将相似的数学情景或相关的数学知识罗列在一起，创造一个可以类比、启发的智能环境，拓开思路，使思维过程发生连锁反应，得出相关的思路和方法，逐步总结出规律性的东西.

三、递归数列的结合

不等式与数列的结合是典型的热点和难点问题.对于数列的研究，本质而言其实依旧是特殊的函数角度的思考，结合不等式进行处理.

例3已知定义域为［0，1］的函数f（x）同时满足：①f（1）=3；②f（x）≥2恒成立；③若x1≥0，x2≥0，x1+x2≤1，则有f（x1+x2）≥f（x1）+f（x2）-2.

（1）试求f（x）的最值；

解析：（1）函数（fx）的最大值是3，最小值是2（.过程略）

用户在使用时，首先呈现的是登录/注册页面，成功登录后进入健康档案主界面。该模块负责管理患者的头像、姓名、身高、体重、年龄、疾病史、体检信息等个人基本信息。

（2）在条件③中，令x1=即故当n∈N*时，有=，即f

（3）对一切x∈［0，1］都有（fx）<2x+2，总存在n∈N，使得，根据（1）（2）可知（fx）≤f且2x+2>2·，故有（fx）<2x+2.

综上所述，对任意x∈［0，1］，（fx）<2x+2恒成立.

说明：观察是认识的开始，是解决问题的基础，可以说科学上的发现大多起源于观察，一般地，通过观察可寻找研究对象的特点和规律，同时观察也是进行比较、类比、联想和归纳的基础，在本题中，我们将传统的、典型的解法进行延拓、整合和创新"-2这种形式平时遇到的比较少，但在数列中，我们经常遇到.根据类比，我们得到f，然后进行迭代，显得一气呵成.解题过程中要把题目所给的信息与基础知识和抽象思维有机地结合起来，形成规律性的解题思路和策略，从而使解题规律化、简明化.

四、导数与不等式

引入了导数工具后，很多以往不能解决的不等式的证明变得轻而易举了，导数工具的使用，将不等式一些证明问题演变成了函数构造及最值的处理，这是导数工具性作用的良好体现.

例4设函数f（x）=（1+x）2-ln（1+x）2.

（1）求函数f（x）的单调区间；

（3）关于x的方程f（x）=x2+x+a在［0，2］上恰有两个相异实根，求a的取值范围.

解析：（1）函数定义域为（-∞，-1）∪（-1，+∞），因为f′（x）=2，由f′（x）>0，得-20，由f′（x）<0，得x<-2或-1

（3）方程（fx）=x2+x+a，即x-a+1-ln（1+x）2=0.记g（x）= x-a+1-ln（1+x）2，则g′（x）=1-由g′（x）>0，得x<-1或x>1，由g′（x）<0，得-1

说明：导数是解决不等式证明问题的利器，从最经典的不等式证明入手：0

总之，“授之以鱼，不如授之以渔”，合理地思考问题解决的方式、积累各种数学思想才能让学生数学学习获得成就.笔者以为，从做题中寻找问题、从问题中进行反思、从反思中提炼归纳，找寻这些问题所反映的知识链接和整合处的收获，目的就是提高解题训练的有效性，从而达到高效低耗的目的；也就是说，通过解答有限道数学题目以获得解答无限道数学问题的解题智慧、解题技能与解题方法，要在做中学，学中思，思后悟.

1.赵栋.数学习题设计与创造性思维培养［J］.中学数学月刊，2012（7）.

2.金凤明.庖丁解牛与数学解题［J］.上海中学数学，2008（4）.

3.殷康康.不等式教学中以形辅数的运用与思考［J］.中学教研，2013（3）.F