导数视角下曲线切线的求解及应用——以解析几何为例说明

筅江苏省宜兴市和桥高级中学　戴栋焱

导数视角下曲线切线的求解及应用——以解析几何为例说明

筅江苏省宜兴市和桥高级中学戴栋焱

众所周知，解析几何中直线与圆锥曲线位置关系是高考数学的重要内容之一.纵观近几年的各省、市的高考试题，直线与圆曲线相切问题经常映入我们的眼帘，对于此类问题的求解关键是切线方程的引入.本文从导数的视角来引入解析几何中曲线的切线.

一、圆的切线方程

过圆x2+y2=r2上的点（x0，y0）的切线方程：对x求导得2yy′=-2x，所以切线的斜率为k=y′=-y0≠0时），所以切线方程为y-y0=-（x-x0），整理得x0x＋y0y＝r2（当y0=0时，亦满足）.同理可得圆（x-a）2+（y-b）2=r2的切线方程为（x-a）（x0-a）+（y-b）（y0-b）=r2.

例1圆x2＋y2＝4的切线与x轴正半轴，y轴正半轴围成一个三角形，当该三角形面积最小时，切点为的坐标P为________.

图1　

解析：如图1，设切点坐标为（x0，y0）（x0>0，y0>0），则切线方程为x0x＋y0y＝4，此时两个坐标轴的正半轴与切线的交点分别为，故其围成的三角形的面积S＝知，当且仅当x0＝y0＝时，x0y0有最大值2，此时S有最小值4，因此点P的坐标为

二、椭圆的切线方程

例2在平面直角坐标系xOy中，点P（x0，y0）（y0≠0）

（Ⅰ）求椭圆C的离心率；

（Ⅱ）若直线l与x轴、y轴分别相交于A，B两点，试求△OAB面积的最小值.

分别相交于A，B两点，所以x0≠0，y0≠0.

所以△OAB的面积S△OAB=

因为点P（x0，y0）在椭圆C所以

三、双曲线的切线方程

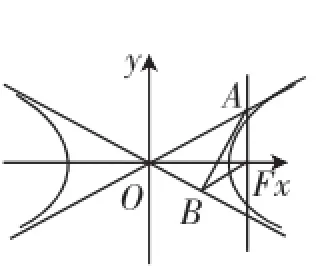
图2　

（Ⅰ）求双曲线C的方程；

（Ⅱ）过C上一点P（x0，y0）（y0≠0）的切线l与直线AF相交于点M，与直线x＝相交于点N，证明：当点P在C上移动时恒为定值，并求此定值.

又P（x0，y0）是C上一点，则

四、抛物线的切线方程

过抛物线y2=2px（p>0）上的点（x0，y）0的切线方程：对x求导得2yy′=2p，所以切线的斜率k=（y≠0时），所以0切线方程为y-y=x-x），整理得yy=p（x+x）（y=0时亦00000成立）.同理焦点在x负轴上的切线方程为yy0=-p（x+x0）；焦点在y轴正半轴上的抛物线的切线方程为：xx0=p（y+y0）；焦点在y轴负半轴上的切线线方程为xx0=-p（y+y0）.

图3　

例4已知抛物线C：y=x2，过点M（1，2）的直线交C与A、B两点，抛物线C在点A处的切线与点B处的切线相交于点P，求△PAB面积的最小值.

解析：如图3，设A（x1，y1），B（x2，y2），则P可以看成是两切线的交点，故可以先求两条切线方程，再求P点坐标.

综上所述，处理圆锥曲线的切线问题，利用导数的几何意义，即在切点的导数值即为在该点的切线的斜率，从而直接引出切线方程.在具体解答时应将切线的推导过程加入解答过程中.Z