一道解析几何最值问题的探究

筅湖北省孝感高级中学　徐运丽

一道解析几何最值问题的探究

筅湖北省孝感高级中学徐运丽

解析几何最值问题是高考常考题型之一，问题求解的基本策略是利用平面几何的几何性质及坐标法将几何问题代数化，进而构造出目标函数，再利用函数最值问题的求解方法解决问题.下面引例说明此类问题的解答.

一、问题展示

题目在平面直角坐标系xOy中，以点A（2，0），曲线y=上的动点B，第一象限内的点C，构成等腰直角△ABC，且∠A=90°，则线段OC长的最大值是______.

本题是以圆为背景的平面解析几何最值问题，根据题意，构造出几何图形，将题目条件与所求直观地展示出来，为后续问题的求解奠定了基础.本题解答中利用三角形全等关系来建立未知点与已知点的联系，进而化未知为已知.

二、分析解答

1.借助图形寻找思维切入点

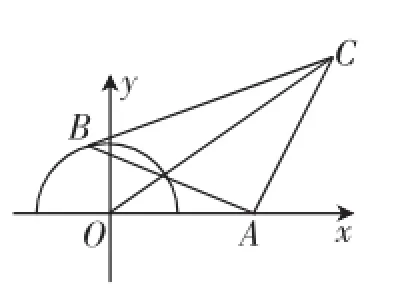
图1　

欲求线段OC长的最大值，应先确定点C的坐标，而点C由定点A与动点B确定，故可从A、B入手，寻找点C的轨迹.

2.挖掘平面几何性质寻找解题思维

图2　

如图2，分别过点B、C作x轴的垂线BD、CE.由角BAC=90°，得∠BAD+∠CAE=90°.而在Rt△CAE中∠ECA+∠CAE=90°，所以∠ECA=∠BAD.

又在Rt△BAD与Rt△ACE中，AB=AC，所以Rt△BAD≌Rt△ACE，所以BD=AE，AD=CE.

设点B的坐标为（m，n），且m2+n2=1，则点C的坐标为（2+n，2-m），所以|OC|=又因为n=所以|OC|=

至此构造出目标函数，将问题转化为函数最值问题来处理.

3.多角度探究目标函数最值

建立平面直角坐标系xOt，如图3考虑平行直线系t=x+b与半圆t=有公共点，则-1≤b≤，即-1≤y≤，所以y的最大值为

解法3：设m=cosθ（0≤θ≤π），则1-m2=sin2θ，故

当x>0，即0

当x<0，即-x>0时，由不等式（*）得1-x2>x2，解得-

三、变式演练

（Ⅰ）求椭圆C的方程；

（Ⅱ）若圆P与x轴相切，求圆心P的坐标；

（Ⅲ）设Q（x，y）是圆P上的动点，当t变化时，求y的最大值.

本题是圆与椭圆的综合问题，解题中需要充分结合圆与椭圆的几何性质，将几何问题代数化，进而构造目标函数来求最值.

（Ⅱ）由题意知，P（0，t）（-1

（Ⅲ）由（Ⅱ）知，圆P的方程x2+（y-t）2=3（1-t2）.因为点Q（x，y）在圆P上，所以y=t±

总之，高考命题常考常新，只要我们充分把握相关问题的处理策略，即可以不变应万变.另外在相关最值问题的求解中，除了上述几种方法外，还有分离常数法、二次函数配方法等，解题中要仔细斟酌、灵活应用.Z

图3