例谈平面几何法解决解析几何问题的几种途径

筅江苏省启东市吕四中学　周华

例谈平面几何法解决解析几何问题的几种途径

筅江苏省启东市吕四中学周华

众所周知，解析几何是高中数学的主要内容，也是历年高考的首选题型.解析几何的本质是用代数方法研究几何问题，数形结合是其主要特征.因此，灵活运用代数知识的同时，充分利用问题中的“几何性质”，往往是解决解析几何问题的关键.在解决高中解析几何问题时，若能够巧妙地运用平面几何知识，不仅能够有效解决问题，而且会使问题变得简洁明了.特别是在高三复习过程中，能将相关知识点联系起来，将平面几何与解析几何融为一体，在提高解题的技能和速度的同时，也使学生解题中感受到数学的无限魅力.下面笔者就从平面几何的一些性质出发，探讨几类解析几何问题的巧妙解法.

一、运用中位线的性质解题

中位线定理是平面几何中较容易掌握和理解的结论，在解析几何题中经常含有中点一类的信息，若能在解析几何中巧妙地加以运用，则会使有关问题变得更加简单容易，利于解题.

解析：如图1，设F′为椭圆的右焦点，连接PF′.

图1　

评注：本解法是从几何角度入手，巧妙地利用了三角形的中位线的性质，充分发挥了数形结合的作用，揭示了题目的本质.

二、运用点的对称性质解题

解析几何经常是点、线之间的关系，经常会涉及点、线的对称问题，若能巧妙用好直线与点的对称问题，就能轻松求解.

例2如图2，使抛物线y=ax2-1（a≠0）上总有关于直线l：x+y=0对称的两点，试求实数a的取值范围.

解析：设P1（x1，y1），P2（x2，y2）是抛物线上关于直线l对称的两点，直线P1P2的方程为y=x+b.

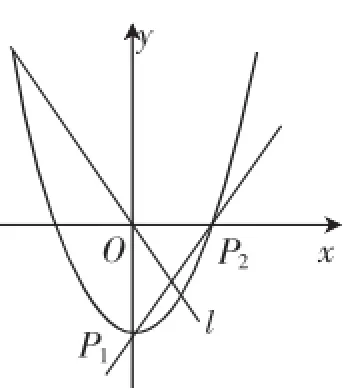
图2　

由韦达定理知x1+x2=

由对称性质知，线段P1P2的中点既在直线P1P2上，又

三、运用矩形图形的性质解题

在解析几何题中，常常会有过已知曲线内某一个定点，作互相垂直的直线一类题，从几何图形看，构造了矩形，就可以用矩形里的性质解题，取得意想不到的效果.

例3已知AC、BD为圆：x2+y2=4的两条相互垂直的弦，垂足为M（1，），则四边形ABCD的面积的最大值为______.

解法一：如图3，S四边形ABCD=

当且仅当AC=BD时取“=”号，且Smax=此时圆心O到AC、BD的距离OE、OF相等，在正方形OEMF中，由OM=，得到OE=

图3　

解法二：如图4，设E、F分别为

AC、BD的中点，则在矩形OEMF中，

OE2+OF2=OM2=3.又AC2+BD2=4（4-

OE）2+4（4-OF）2=20，则S四边形ABCD=当且仅当AC=BD时，取“=”号.

图4　

评注：在解题时，需要灵活思考，解法一巧用基本不等式及特殊的纯几何图形直接求解，解法二是在解法一的基础上优化了解题过程，变正方形为矩形.可见，在解决解析几何题时，我们不妨考虑得细致一点儿，方法多样一点儿，则能灵活解决相关问题.

四、运用线段垂直平分线性质解题

垂直平分线定理是平面几何中常见并且运用较为广泛的定理，也是我们熟知的定理，若能在解析几何中巧妙运用，则可避开复杂运算，使解答直观容易.

例4如图5，A、B是两个定点，且|AB|=2，动点M到点A的距离是4，线段MB的垂直平分线l交MA于点P，直线k垂直于直线AB，且点B到直线k的距离为3.求证：点P到点B的距离与到直线k的距离之比为定值.

证明：以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系，则A（-1，0），B（1，0）.

图5　

因为直线l为线段MB的垂直平分线，所以|PM|=|PB|，所以|PA|+|PB|= |PA|+|PM|=|MA|=4.

所以点P的轨迹是以A、B为两焦点，长轴为4的椭圆，易求其方程为=1，直线k是椭圆的准线.根据定义知，点P到点B的距离与到直线k的距离之比为e=

评注：本题巧妙地运用垂直平分线定理及椭圆定义很快使问题获解.

五、运用圆和三角形有关性质解题

圆和三角形是平面几何中的基本图形，也是解析几何问题中常见的“构造”元素，所以圆和三角形的有关性质的应用，在解析几何问题中是十分重要的.例如，解析几何中曲线上的两动点连线过定点问题是高考考查的重点内容之一，是近年来高考、竞赛的常见题.此类问题定中有动，动中有定，常与轨迹问题、曲线系问题相结合，深入考查直线与圆、圆锥曲线的关系等相关知识，若利用图形中的几何特征来解题能起到事半功倍的作用.

例5如图6，在平面直角坐标系xOy中，已知圆C：x2+y2=r2和直线l：x=a（其中r和a均为常数，且0＜r＜a），M为l上一动点，A1、A2为圆C与x轴的两个交点，直线MA1、MA2与圆C的另一个交点分别为P、Q，求证：直线PQ过定点，并求出该定点的坐标.

图6　

分析：此题解法很多，若按照解析几何的基本思路循规蹈矩，即用代数方法解决几何问题，设出点的坐标，找出题目中的关系，转化为代数关系式，解得结果.思路简单、清晰，学生易上手，但由于题中涉及的未知量较多，因此运算过程复杂，计算量大，需要学生有足够的耐心和细心，一般学生很难解到最终结果（具体解法略），若能关注到图形的几何特征即可很快得到结果.

证明：运用圆直径所对的圆周角是直角，建立代数关系，列出动点P、Q满足的曲线系方程，求出动直线PQ的方程，得出定点.

由题设可知，A1（-r，0），A2（r，0），设M点的坐标为（a，t），直线MA1的斜率为k1，MA2的斜率为k2，则MA1的方程为y=k1（x+r），过点M（a，t），则t=k1（a+r），得到k1=

MA2的方程为y=k2（x-r），过点M（a，t），则t=k2（a-r），得到k2=.连接AQ并延长交直线x=a与N，如图6所示，

由于A1A2是圆C的直径，A1Q⊥MQ，所以直线A1Q的方程为y=-

（x+r），将k2代入，即y=-x+r），得N点坐标为

同理，连接PA2并延长交直线x=a于点N′，得直线PA2的方程为y=-可知N′的坐标为⊥，所以N和N′实际为同一点.

根据几何特征，P、Q、N、M四点共圆，P、Q在以MN为直径的圆上，即（x-a）2+（y-t）

所以PQ为两圆的交线，求得PQ的方程为（x-a）2+（y-令 y=0，得x=，故直线PQ恒过定点

评注：在解析几何题设中均隐藏着一些特定的几何特征.利用图形中的几何特征，寻找代数关系，真正体现了数形结合的思想.避开烦琐复杂的整理、转化的过程，而借助于几何特征建立曲线系，设而不解，运算的量小，不易出错.这种方法在很多题目中都可应用，在解析几何繁杂的运算中利用图形的几何特征解题将起到事半功倍的作用.

六、利用平行线分线段成比例的性质解题

平行线分线段成比例是初中几何的一个重点内容，而在解析几何中若能巧用此定理，则可减少计算量，降低解题难度.

图7　

（Ⅰ）求椭圆C的方程；

（Ⅱ）求线段MN的长度的最小值；

（Ⅲ）当线段MN的长度最小时，在椭圆C上是否存在这样的点T，使得△TSB的面积为？若存在，确定点T的个数；若不存在，说明理由.

（Ⅱ）如图8，过点S作SE垂直于x轴，设S（x0，y0），显然SE∥l，则有

图8　

评注：第（Ⅱ）问巧妙运用平行线分线段成比例，找出线段与线段的相等关系，从而得到结论，大大减小运算量，使解题速度大大提高.此解法体现的另一思路是圆锥曲线中与顶点相关的线段可以考虑将圆锥曲线的方程变形，然后用平方差公式得到相关比例，使解题的运算量大大减小.

七、利用角平分线有关性质解题

角平分线定理在初中虽然仅出现在习题中，但它在高中内容中时常出现，若作为结论加以介绍，并学会应用，将使解决有关问题变得简单易行.

图9　

解析：如图9，因为I为△F1F2P的内心，连接F1I，F2I，则F1I、F2I、PI分别是三角形F1F2P的角平分线，由角平分线的性质定理可得，即所以

评注：本题结合角平分线定理，使问题简单明了，角平分线定理可以用正弦定理证明，便于理解和记忆.

总之，解析几何中，“解析”只是方法，“几何”才是本质.平面几何在教学目标上侧重于培养学生的作图识图能力和逻辑推理能力.只有利用平面几何相关知识，正确把握问题中各个对象的位置关系，并转化出其内在的数量关系，才能用解析的方法顺利解决问题.教学中若利用平面几何知识可避免烦琐计算，收到意想不到的解题效果；这样不仅能起到变难为易、化繁为简的作用，还有助于打破学生学习过程中易于形成的一种思维定势，有益于学生的发散性思维的培养.F