一道立体几何最值问题的拓展探究

筅江苏省丹阳高级中学　朱炜俊

一道立体几何最值问题的拓展探究

筅江苏省丹阳高级中学朱炜俊

立体几何中体积最值问题能有效考查学生的空间想象能力、数形结合能力，以及函数与方程思想的理解和掌握程度，因此在高考中备受命题人的关注，本文以一道课本练习题为引例，就此类问题的求解拓展探究.

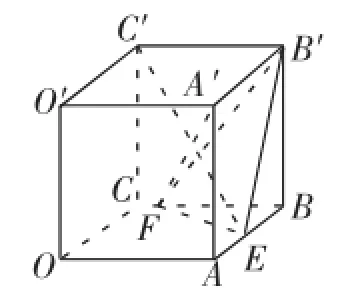
图1　

图2　

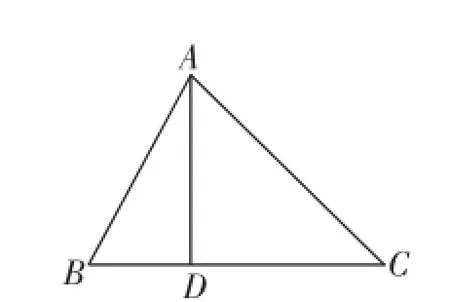
例1（课本练习题）如图1，在棱长为a的正方体OABC-O′A′B′C′中E、F分别是棱AB、BC上的动点，且AE=BF.

（1）求证：A′F⊥C′E；

（2）当三棱锥B′-BEF的体积取最大时，求二面角B′-EF-B的正切值.

解析：（1）略.

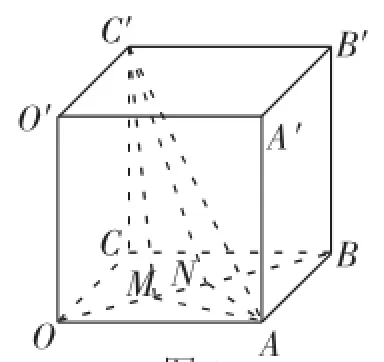
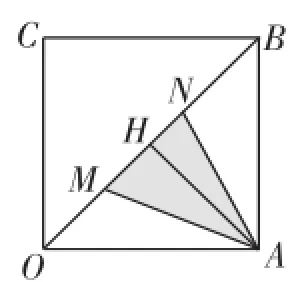
（2）已知三棱锥B′-BEF的高BB′为定值，欲使其体积最大，则其底面积BEF最大.如图2所示，在正方形OABC中，设AE=BF=x（0

方法1：利用二次函数的性质，可知当x=a时，S取得2最大值

以下利用空间向量法求二面角B′-EF-B的正切值.（过程略）

评注：解答此类问题的关键是据所给的条件，构造目标函数，再利用函数求最值的方法求解，如二次函数配方法、均值不等式法、三角函数最值法、分离常数法、导数法等方法求解.下面对此题进行变式探究.

一、变化动点位置

图3　

例2如图3，在棱长为2的正方体OABC-O′A′B′C′中，M、N分别为线段OB上的点，若∠MAN= 30°，则三棱锥C′-AMN体积的最大值为______.

解析：因为三棱锥C′-AMN的高为定值，则其体积最大时，其底面积AMN取最大值.

VC′-AMN=AN.

过点A作AH垂直OB于点H，如图4，易知，当MN取最大值时，三角形AMN的面积最大.不妨设∠MAH＝

图4　

评注：本题将例1中动点的位置置于对底面的对角线OB上，将空间问题平面化后，利用解三角形知识求解，使体积最值转化为三角形面积最值问题，通过面积公式构造三角函数关系，再借助函数y=Asin（ωx+φ）的性质求解，求解过程中注意角的范围变化，防止错解.

二、改变求解结论

例3如图3，在棱长为2的正方体OABC-O′A′B′C′中，M、N分别为线段OB上的点，若∠MAN=30°，则三棱锥C′-AMN体积的最小值为_______.

同例2解答，如图4，过点A作AH垂直OB于点H，易知，当MN取最小值时，三角形面积最小，不妨设∠MBH＝ α，∠NBH=β，由AH=所以，当且

评注：本题将例2所求结论改为最小值，同样利用例2的解答方法，即构造三角函数求最值.在一道题目解答完毕后，通过对题目的条件或结论进行变式探究，能有效地考查同学们利用所学知识灵活解答问题的能力.

三、变换求解方法

例4同例3.

图5　

由面积公式得S△AMN=xysin30°，所以S△AMN=·MN=xysin30°，所以xy=2MN.

由余弦定理可得MN2=x2+y2-2xycos30°=x2+y2-

所以VP-BMN的最小值为

评注：对一道题通过从不同角度进行分析解答，即一题多解训练，有利于培养同学们的发散思维，有利于建立不同知识点之间的关联，从而形成解题思维和解题能力的提高.

四、问题拓展延伸

例5如图6，∠ACB＝45°，BC＝3，过动点A作AD⊥BC，垂足D在线段BC上且异于点B，沿AD将△ABD折起，使∠BDC＝90°，连接BC（如图7所示）.

图6　

图7　

（1）当BD的长为多少时，三棱锥A-BCD的体积最大？

（2）当三棱锥A-BCD的体积最大时，设E、M分别为棱BC、AC的中点，试在棱CD上确定一点N，使得EN⊥BM，并求EN与平面BMN所成角的大小.

解析：（1）在如图6所示的△ABC中，设BD＝x（0＜x＜3），则CD＝3-x.

由AD⊥BC，∠ACB＝45°，知△ADC为等腰直角三角形，所以AD＝CD＝3-x.

由折起前AD⊥BC，知折起后，AD⊥DC，AD⊥BD，且BD∩DC＝D，所以AD⊥平面BCD.又∠BDC＝90°，所以，当且仅当2x＝3-x，即x＝1时，等号成立.

故当x＝1，即BD＝1时，三棱锥A-BCD的体积最大.

（2）略.

评注：据题构造出目标函数后，利用均值不等式的三元形式，即a，b，c>0，a+b+c

（当且仅当a=b=c时，“=”成立）求函数最值.

总之，求立体几何最值问题的方法是根据所给条件确定目标函数，再利用相关方法求目标函数的最值，除本文所述的几种方法外，同学们在学习中要不断进行归纳总结，以不变应万变，提高自己的应试能力.F