三角形背景下的最值问题探究

筅江苏省扬中市第二高级中学　蔡飞

三角形背景下的最值问题探究

筅江苏省扬中市第二高级中学蔡飞

解三角形问题中的最值（取值范围）问题是高考重点题型之一，它不仅与解三角形自身的常见的基础知识密切相关，而且与代数及一些几何中的有关性质密切联系.这类问题综合性较强，解法灵活，对考生能力要求较高.本文针对近几年来高考试题中涉及解三角形问题中的面积、角、角的三角函数值、边长、周长的最值（取值范围）问题的求解策略进行归纳，以提高同学们的思维能力和解题能力.

一、利用均值不等式

例1设△ABC中的内角A，B，C所对的边长分别为a，b，c，且cosB=，b=2.

（2）求△ABC面积的最大值.

因为a＜b，所以A是锐角，所以A=30°.

因为b2=a2+c2-2accosB，所以4=a2+c2-ac.

因为a2+c2≥2ac，所以2ac-ac≤4，所以ac≤10，当a=c=时等号成立.

所以△ABC面积的最大值为3.

评注：均值不等式是高考重要考查点之一，其主要形式是a+b≥2（a，b>0）及a2+b2≥2ab（a，b∈R），应用其解题时要注意定理的适用条件，即“正”“定”“等”的判断.本题求解中将余弦定理与均值不等式相结合.

变式在△ABC中，a，b，c分别是角A，B，C的对边，且a+c=2b.

（1）求cosB的最小值；

（2）略.

二、构造三角函数

例2如图1，在等腰直角△OAB中，∠OAB＝90°，OA＝2，M、N分别为线段OB上的点，若∠MAN=30°，则△AMN面积的最小值为_______.

如图1，过点A作AH垂直OB于B点H，不妨设∠MAH＝α，∠NAH=β.

图1　

评注：本题求解中通过引入角度α，β，利用解三角形相关知识，构造出面积函数，进一步再将其转化为y= Asin（ωx+φ）型求最值.另外本题也可利用均值不等式法求解：如图1，设AN=x，AM=y，因为OB=2，所以OB上的高h=，由面积公式得S=xysin30°，所以S=△AMN△AMN所以xy=2MN.由余弦定理可得所以MN≥，当且仅当x=y时取等号.所以S△AMN≥

三、利用二次函数

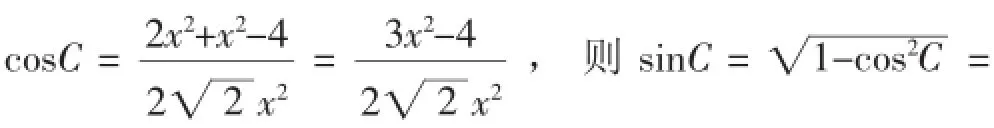
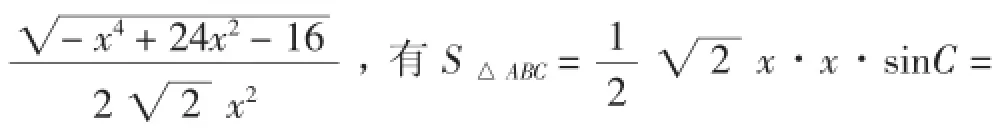
图2　

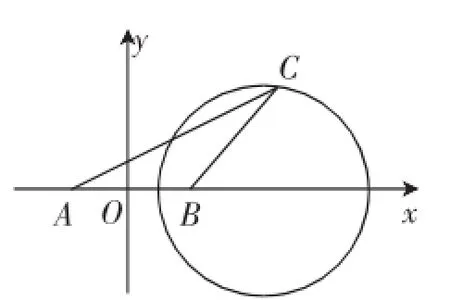
图3　

评注：求解最值（取值范围）问题，有时可先把所求解的问题转化为二次函数问题，再利用配方法求最值.另外注意到S=AB×h=h（h为BC边上的高），问题转化为求h的最大值，可以尝试判断满足AC=BC的动点C的运动轨迹，即借助解析法求解：如图3，以AB边所在直线为x轴，AB边的中垂线为y轴建立平面直角坐标系，则A（-1，0）、B（1，0）.设C（x，y）.由条件AC=BC，得整理得（x-3）2+ y2=8（x≠0），即动点C的轨迹是以点（3，0）为圆心、2姨2为半径的圆（不含与x轴的两个交点）.所以S=AB·|y|= |y|≤2，即x=3时，△ABC的面积最大，最大值为2

四、利用导数

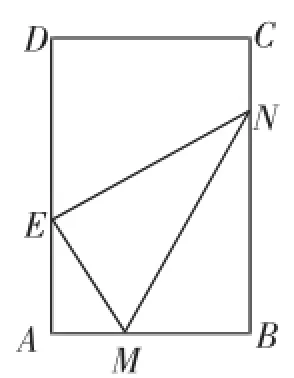
图4　

例4已知矩形纸片ABCD中，AB=6cm，AD=12cm，将矩形纸片的右下角折起，使该角的顶点B落在矩形的边AD上，且折痕MN的两端点M、N分别位于边AB、BC上，设∠MNB=θ，MN=l.

（1）试将l表示成θ的函数；

（2）求l的最小值.

解析：（1）如图4所示，∠MNB=θ，则∠ENB=2θ，在四边形MBNE中，∠ENB+∠BME=180°，∠EMA+∠BME=180°.所以∠AME=2θ，根据锐角三角函数定义，知MB=lsinθ，AM=l·sinθcos2θ.

由题设得lsinθ+l·sinθ·cos2θ=6，从而可得l=

评注：导数法是求函数单调区间、极值、最值、零点等问题的有力工具.在解答解析几何最值问题时，将几何问题代数化后，构造出的目标函数若为高次函数，则可借助导数法求解.

综上，三角形边、角、面积等取值范围或最值问题是高考考查的重、难点之一.此类问题的形式灵活，且注重与函数、不等式和几何等知识的交汇融合.求解时往往需要结合平面几何的几何性质、基本不等式，以及函数值域与最值等相关知识，并充分利用正余弦定理、面积公式、三角形的内角和定理等，以实现几何问题与代数问题的有效转化.F