引射吸水室对离心泵性能的影响

牟介刚，王荣，谷云庆，郑水华，刘菲，汪洋

(浙江工业大学 机械工程学院，浙江 杭州，310014)

引射吸水室对离心泵性能的影响

牟介刚，王荣，谷云庆，郑水华，刘菲，汪洋

(浙江工业大学 机械工程学院，浙江 杭州，310014)

以IS100−80−160离心泵为模型载体，提出一种引射吸水室离心泵。基于RNG k−ε湍流模型对不同引射参数下离心泵内部流场进行数值模拟，研究引射口直径和引射角度对离心泵汽蚀及水力性能的综合影响，并对数值计算模型进行实验验证。研究结果表明：在设计工况下，随着引射口直径的增大，泵汽蚀余量先减小后增大，扬程和效率略有下降；当引射口直径为3 mm时，引射吸水室的增压效果最好，泵汽蚀性能最佳；随着引射角度的增大，泵汽蚀余量逐渐增大，扬程和效率略微下降，合理的引射角度为15°～30°；实验与数值模拟结果的变化趋势相吻合，验证了数值模拟的准确性。

离心泵；引射；汽蚀；数值模拟

离心泵汽蚀不仅影响泵的工作特性，还产生振动、噪声等，甚至直接导致泵停止运行，其一直是离心泵研究中致力解决的难点之一[1−2]。目前，国内外主要从使用耐汽蚀材料和优化设计叶轮结构2方面来研究离心泵汽蚀，其中对结构参数的研究尤为显著。在耐汽蚀材料研究方面，STELLA等[3]通过不同的铸造方式，对CuSnNi合金的表面磨损和耐汽蚀性能进行了实验研究。LAGUNA−CAMACHO等[4]对不同的工程材料如纯铝、1045钢、铝合金等进行了大量的汽蚀实验。NEVILLE等[5]研究了液体中含有的固体颗粒和气泡汽蚀对钛合金的损害。王飚等[6]利用光学显微镜、扫描电镜、电子探针和X线衍射对一些材料的汽蚀和磨蚀后样进行了微观分析研究。在结构参数研究方面，郭晓梅等[7]对不同结构参数的双叶片诱导轮进行了内部三维不可压湍流流动数值计算。崔宝玲等[8]采用闭式流体输送试验台，对具有前置诱导轮的高速离心泵进行了汽蚀特性实验研究，探讨了无诱导轮、单个及串联诱导轮这3种工况下诱导轮对离心泵性能及汽蚀的影响。曹卫东等[9]在不同结构模型下对叶轮内的空化进行数值模拟，表明径向回流平衡孔能够明显改善离心泵的汽蚀性能。AIFAYEZ等[10−11]应用声发射、振动分析等先进实验技术对汽蚀进行了深入研究。ESCALER等[12]认为，应当根据介质、泵比转速以及叶轮外径进行修正才能更准确地描述泵的汽蚀特性。近年来，引射技术[13−14]日臻成熟，并成功运用于国民经济的多个领域，取得了较好的发展成果。崔宝玲等[15]通过实验研究表明：在吸水室加设1个引射装置可以明显改善离心泵汽蚀性能，不同的引回流量对离心泵的汽蚀性能有较大影响。吴昱等[16]通过理论分析认为在吸水室增置一引射结构，将泵出口的少量高能液体引回到泵入口可以改善离心泵的汽蚀性能。尽管目前已有一些引射吸水室改善离心泵汽蚀性能的研究成果，但对于引射吸水室的关键参数，如引射口直径、引射角度等确定的方法还不成熟，并忽略了引射吸水室改善离心泵汽蚀时其对离心泵水力性能等的综合影响[17]。针对以上原因，本文作者结合数值模拟方法，对引射离心泵汽蚀和内部流场进行数值模拟，分析引射吸水室对离心泵汽蚀及水力性能的综合影响，确定最佳引射口直径及引射角度。

1　模型建立及参数设置

1.1引射结构计算模型

图1所示为引射吸水室结构示意图。引射管将离心泵出口处的少量高压液体引回后，在离心泵吸入口的混合区域通过引射口喷射与低压液体汇集，汇集的混合液体通过质点间的相互碰撞来传递能量，并随着流动的连续最终提高泵入口处液体的压力，减小泵进口前后的压力降，进而降低泵汽蚀余量。其中，引射吸水室的重要参数有引射口直径d和引射角度β等。

图1　引射吸水室结构示意图Fig. 1 Schematic diagrams of ejector suction chamber

选取单级单吸离心泵IS100−80−160为计算原模型，其基本性能参数如表1所示。

表1　IS100−80−160离心泵基本性能参数Table 1 Basic performance parameters of IS100−80−160 centrifugal pump

分别以β=30°，d=2，3，4和5 mm及d=3 mm，β=15°，45°，60°和75°为研究方案，应用CFX对模型泵的扬程H、效率η以及汽蚀余量进行预测，分析引射吸水室对离心泵性能的影响，确定最佳的d和β。

1.2计算方程

涉及的计算方程主要有控制方程、湍流模型、气泡动力学模型和汽蚀模型这4种。对于不可压缩流体，流体流动过程中满足以下连续性方程和动量方程：

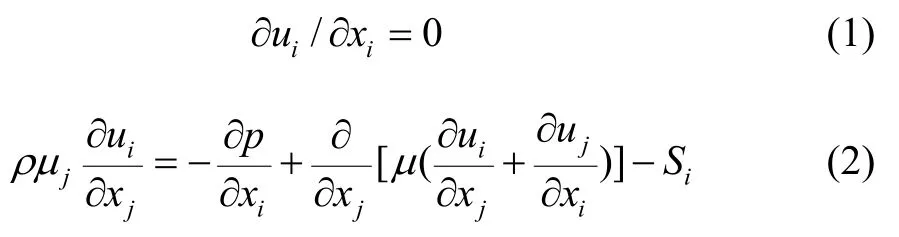
式中：ρ为流体密度；xi和xj为坐标(i和j为坐标轴方向)；ui和uj为时均流速；p为流体压力；μ为流体动力黏度；Si为广义源项。

对于离心泵的数值模拟，RNG k−ε湍流模型可以更好地处理高应变率及流线弯曲程度较大的流动，其湍动能和湍流耗散率的约束方程分别为：

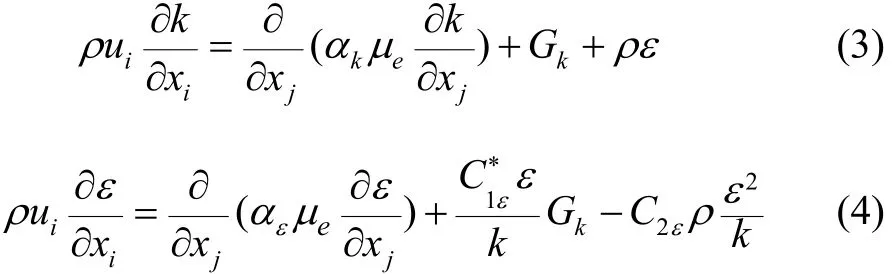
其中的增项为：

式中：k为湍动能；ε为耗散率；Gk为平均速度梯度引起的k的产生项；μe为湍流黏性系数；为控制项；其余为常数，Cμ=0.084 5，αk=αε=1.39，C1ε=1.42，C2ε=1.68，η0=4.377，γ=0.012。

采用Rayleigh−Plesset方程模拟气泡的生长和溃灭，方程为

二阶项和表面张力相对于方程整体来说很小，可忽略不计，故式(8)可变为

式中：R为气泡半径；t为时间；pv为常温液体的汽化压力；σ为气体与液体之间的表面张力系数。

1.3网格划分及参数设置

计算流体域采用分块化网格划分的方法，流道复杂、扭曲程度较高的叶轮、蜗壳及引射管采用非结构化网格，进水管、吸水室、回流管和出水管采用结构化网格。采用四面体或四面体与六面体网格共用以防止网格畸形，对隔舌进行局部加密处理。各区域网格在交界面上点对点搭接，在保证方便处理的同时可保证方程守恒。考虑计算机的性能，对计算模型进行网格无关性分析。选取7组不同网格数量的实验组进行数值模拟，通过逐渐加密流体域网格的方式，直到扬程和效率受网格数影响较小为止，其结果如表2所示。

由表2可知：当网格数大于1.17×106之后，扬程和效率的变化受网格数影响相对较小，趋于稳定。故选定模型泵的计算单元总数为1 170 823个，其中进水管单元为156 001个，叶轮单元为295 940个，蜗壳单元为545 181个，出水管单元为173 701个。

表2　网格数对H和η的影响Table 2 Influence of numbers of grids on H and η

计算流体为25 ℃的清水和25 ℃的空气，pv= 3.574 kPa，气泡的平均直径为2 μm，参考压力设为0 Pa，求解控制时间步长设置为物理时间3.3 ms，收敛精度为1×10−4。进口边界条件采用总压进口，液体的体积分数设为1，气体的体积分数设为0，通过不断降低进口压力的方式使离心泵发生汽蚀，出口边界条件采用质量流量出口，以保证泵运行时流量恒定，固壁边界条件采用无滑移边界。

2　结果与分析

2.1引射口直径对离心泵性能的影响

图2所示为不同d时的数值模拟曲线。由图2可知：d对汽蚀余量影响较大；汽蚀余量随着d的增大呈先减小后增大的趋势；当d=3 mm时，汽蚀余量达最小值2.46 m，此时泵的汽蚀性能最佳，与原模型泵汽蚀余量为4.00 m相比，降低了1.54 m，但随着d的增大，H和η都略有下降；当d≥4 mm时，汽蚀余量的状况就会有所恶化。这是由于当d较大时，引回液体流量增加，使吸水室和管路中的水力损失和冲击损失增大，吸入口液流流动更加紊乱等，造成η和H下降、汽蚀余量恶化。

图3和图4所示分别为泵进口总压为26 kPa，在设计工况下，不同d时，叶轮中截面的静压云图和气泡体积分布云图。由图3和图4可知：叶轮进口静压分布不均匀，d不同时叶轮中截面的静压分布趋势一致，从叶轮出口到叶轮进口的静压逐渐降低。但是，随着d的增大，同一半径处的静压先增大后减小，当d=3 mm时，静压达到最大。叶轮进口低压区域也随着d的增大呈现先减小后增大的趋势，当d=3 mm时，叶轮进口低压区域最小。这是因为气泡只在叶片进口背面很小的区域内产生和溃灭，这也验证了当d=3 mm时，引射吸水室的增压效果最好，泵的汽蚀性能最佳。且汽蚀初生时，气泡只在叶片进口背面一个很小的低压区域内产生，当d不同时，叶轮中截面的气泡体积分布趋势一致。叶轮进口背叶面处气泡体积分数最大，因为此处的曲率半径最大，过流面积最小，液流速度最大，静压最低，故产生的气泡最多。与静压分布趋势相似，叶轮流道产生气泡的区域随着d的增大先变小后变大，当d=3 mm时，叶轮流道产生气泡的区域最小。另一方面，在同一半径处，气泡体积分数先减小后增大，当d=3 mm时，叶轮流道气泡体积分数最小。

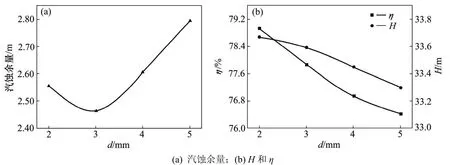
图2　不同d时的数值模拟曲线Fig. 2 Numerical simulation curves under different d

图3　不同d时叶轮中截面的静压云图Fig. 3 Static pressure contours of cross section of impeller under different d

2.2引射角度对离心泵性能的影响

图5所示为不同β时的数值模拟曲线。由图5可知：汽蚀余量随着β的增大而逐渐增大。当β较小时，汽蚀余量较小，H和η较高。随着β增大，H和η略微下降，但是下降的幅度很小，在β=15°和30°的情况下，H和η分别只下降0.2 m和0.19%，因此，可以认为，H和η受β的影响有限。当β增大到一定程度后继续增大时，汽蚀余量几乎呈指数关系增大，直到β超过75°时，汽蚀余量超过2.94 m，汽蚀性能恶化。这是由于当β过大时，引回的高压液体与低压液体产生冲击、碰撞等，进而产生气泡、漩涡，不但加大了能量损失，更使气泡被吸入。显然，β越小越好，但在兼顾水力性能、工艺难度等多因素情况下，β的合理范围为15°～30°。

图4　不同d时叶轮中截面的气泡体积分布云图Fig. 4 Bubble volume distribution contours of cross section of impeller under different d

图5　不同β时的数值模拟曲线Fig. 5 Numerical simulation curves under different β

图6和图7所示分别为泵进口总压为26 kPa，在设计工况下和不同β时，叶轮中截面的静压云图和气泡体积分布云图。由图6和图7可知：同一半径处静压随着β的增大而逐渐降低，当β=75°时静压最低，当β=15°时叶轮进口低压区域最小。叶轮进口低压区域的面积随着β的增大而逐渐变大，证实了β越小，引射吸水室的增压效果和离心泵的汽蚀性能越好。气泡体积分数在叶轮进口叶片背面处最大，不同β时叶轮中截面的气泡体积分数分布趋势一致，并且在叶轮流道内向叶片工作面逐渐降低。与静压分布趋势相似，叶轮流道产生气泡的区域面积随着β的增大而逐渐变大，当β=75°时，叶轮流道产生气泡的区域最大。另一方面，同一半径处气泡体积分数也随着β的增大逐渐增大，当β=75°时的叶轮流道气泡体积分数最大。这说明，若β过大，引射吸水室不但达不到增压效果，还可能会恶化离心泵的汽蚀性能。

图6　不同β时叶轮中截面的静压云图Fig. 6 Static pressure contours of cross section of impeller under different β

图7　不同β时叶轮中截面的气泡体积分布云图Fig. 7 Bubble volume distribution contours of cross section of impeller under different β

3　实验结果及分析

3.1实验装置及方法

实验在浙江水泵总厂有限责任公司进行，该公司的实验装置符合国家标准GB/T 3216—2005[18]，测试精度为1级，采用闭式回路。在设计工况下，分别取β=30°，d=2，3，4和5 mm及d=3 mm，β=15°，45°和60°进行汽蚀及性能实验，以验证数值模拟的准确性。在密闭容器内用抽真空的方法来逐渐降低装置汽蚀余量，使泵发生汽蚀空化。直至恒定流量下的扬程下降3%，此时汽蚀余量近似等于临界汽蚀余量。在实验过程中需测量进出口压力、扭矩、转速等参数。

3.2实验分析

图8所示为不同d时实验值曲线与数值模拟值曲线的对比。由图8可知：实验结果与数值模拟结果的变化总趋势一致。其中，汽蚀余量数值模拟值与实验值的差值范围为−0.17～0.05 m，最大偏差为6.47%，发生在d=2 mm处。H数值模拟值与实验值的差值范围为1.11～1.97 m，η数值模拟值与实验值的差值范围为0.79%～2.92%；当d=5 mm时，H和η的最大偏差分别为5.92%和3.82%。

图9所示为不同β时实验值曲线与数值模拟值曲线的对比。由图9可知：实验结果与数值模拟结果的变化总趋势相吻合。不同β时汽蚀余量数值模拟值与实验值的差值范围为−0.18～−0.05 m，最大偏差为7.12%，发生在β=45°处。H数值模拟值与实验值差值范围为0.73～2.22 m，η的差值范围为0.16%～1.95%，当β=60°时，H和η的最大偏关分别为6.63%和2.51%。

图8　不同d时的数值模拟曲线与实验曲线的对比Fig. 8 Comparisons between numerical simulation curves and experimental curves under different d

图9　不同β时的数值模拟曲线与实验曲线的对比Fig. 9 Comparisons between numerical simulation curves and experimental curves under different β

在设计工况下，汽蚀余量的实验值略高于数值模拟值，H和η的实验值略低于数值模拟值，这是因为数值模拟时简化了计算模型，忽略了过流部件的粗糙度等因素的影响。再者，离心泵的性能实验是比较复杂的过程，还受多种因素如操作误差、设备误差、环境条件等方面的影响。从对比结果来看，数值模拟值与实验值的最大偏差为7.12%。

4　结论

1) 引射吸水室可有效提升离心泵汽蚀性能，但扬程和效率略有下降。引射口直径和引射角度对离心泵性能影响较大，为引射吸水室的重要参数。

2) 随着d的增大，泵汽蚀余量先减小后增大，当d=3 mm时，叶轮进口低压区域和流道产生气泡体积分数最小，引射吸水室的增压效果最好，泵汽蚀性能最佳。

3) 随着β的增大，泵汽蚀余量、气泡体积分数和叶轮进口低压区域的面积逐渐增大，同一半径处的静压逐渐降低，最佳β的范围为15°～30°。

4) 在设计工况下，泵汽蚀余量，H及η的实验值与数值模拟值的变化趋势相吻合。数值模拟值与实验值的最大偏差为7.12%，数值模拟具有正确性。

[1] ASKEW J. Centrifugal pumps: avoiding cavitation[J]. World Pumps, 2011, 2011(7/8): 34−39.

[2] 潘中永, 倪永燕, 汤跃, 等. 离心泵汽蚀余量计算与预测[J].农业机械学报, 2008, 39(12): 206−209. PAN Zhongyong, NI Yongyan, TANG Yue, et al. The calculation and prediction of centrifugal pump NPSH[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(12): 206−209.

[3] STELLA J, GERKE L, POHL M. Study of cavitation erosion and adhesive wear in CuSnNi alloys produced by different casting processes[J]. Wear, 2013, 303(1/2): 541−545.

[4] LAGUNA−CAMACHO J R, LEWIS R, VITE−TORRES M, et al. A study of cavitation erosion on engineering materials[J]. Wear, 2013, 301(1/2): 467−476.

[5] NEVILLE A, MCDOUGALL B A B. Erosion-and cavitationcorrosion of titanium and its alloys[J]. Wear, 2001, 250(1): 726−735.

[6] 王飚, 王宇栋, 张自华, 等. 抗磨蚀材料失效过程的微观特性[J]. 中国工程科学, 2001, 3(8): 82−86. WANG Biao, WANG Yudong, ZHANG Zihua, et al. Failure processes micro-characteristic studies of two materials to resist cavitation erosion and to resist erosion and abrasion[J]. Engineering Science, 2001, 3(8): 82−86.

[7] 郭晓梅, 朱祖超, 崔宝玲, 等. 诱导轮内流场数值计算及汽蚀特性分析[J]. 机械工程学报, 2010, 46(4): 122−128. GUO Xiaomei, ZHU Zuchao, CUI Baoling, et al. Analysis of cavitation and flow computation of inducer[J]. Chinese Journal of Mechanical Engineering, 2010, 46(4): 122−128.

[8] 崔宝玲, 万忠, 朱祖超, 等. 具有诱导轮的高速离心泵汽蚀特性试验[J]. 农业机械学报, 2010, 41(3): 96−99. CUI Baoling, WAN Zhong, ZHU Zuchao, et al. Research on suction performance of high speed centrifugal pump with inducer[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010, 41(3): 96−99.

[9] 曹卫东, 张晓娣, 高一, 等. 径向回流平衡孔低比转数离心泵空化性能研究[J]. 农业机械学报, 2012, 43(1): 37−41. CAO Weidong, ZHANG Xiaodi, GAO Yi, et al. Cavitation performance of the low specific-speed centrifugal pump with radial reflux balance hole[J]. Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(1): 37−41.

[10] AIFAYEZ L, MBA D, DYSON G. The application of acoustic emission for detecting incipient cavitation and the best efficiency of a 60 kW centrifugal pump case study[J]. NDT & E International, 2005, 38(5): 354−358.

[11] FARGE M, SCHNEIDER K. Coherent vortex simulation(CVS), a semi-deterministic turbulence model using wavelets[J]. Flow, Turbulence and Combustion, 2001, 66(4): 393−396.

[12] ESCALER X, EGUSQUIZA E, FARHAT M, et al. Detection of cavitation in hydraulic turbines[J]. Mechanical Systems and Signal Processing, 2006, 20(4): 983−1007.

[13] 吴革生, 种道彤, 刘双全, 等. 高效开采低压天然气引射装置的试验研究[J]. 工程热物理学报, 2009, 30(6): 974−976. WU Gesheng, ZHONG Daotong, LIU Shuangquan, et al. Experimental investigation of efficient injector of low pressure natural gas[J]. Journal of Engineering Thermophysics, 2009, 30(6): 974−976.

[14] 谷云庆, 赵刚, 郑金兴, 等. 射流表面主流场速度与射流速度耦合减阻特性[J]. 中南大学学报(自然科学版), 2012, 43(12): 4713−4721. GU Yunqing, ZHAO Gang, ZHENG Jinxing, et al. Characteristics of drag reduction on coupling of jet surface main flow field velocity and jet velocity[J]. Journal of Central South University (Science and Technology), 2012, 43(12): 4713−4721.

[15] 崔宝玲, 朱祖超, 吴昱, 等. 引射装置的试验研究[C]//中国工程热物理学会流体机械学术会议. 西安: 中国工程热物理学会流体机械学术会议, 2004: 227−230. CUI Baoling, ZHU Zuchao, WU Yu, et al. Experimental investigation of jetting device[C]// The Fluid Mechanics Conference of Chinese Engineering Thermophysics. Xi’an: Fluid Mechanics Conference of Chinese Engineering Thermophysics, 2004: 227−230.

[16] 吴昱, 朱祖超. 利用引射结构提高离心泵的汽蚀性能[J]. 工程设计学报, 2002, 9(2): 86−88. WU Yu, ZHU Zuchao. Improving suction performance of centrifugal pumps by using jetting device[J]. Chinese Journal of Engineering Design, 2002, 9(2): 86−88.

[17] KESY A, KOTLINSKI J. Mechanical properties of parts produced by using polymer jetting technology[J]. Archives of Civil and Mechanical Engineering, 2010, 10(3): 37−50.

[18] GB/T 3216—2005, 回转动力泵水力性能验收试验(1级和2级)[S]. GB/T 3216—2005, Rotodynamic pumps−hydraulic performance acceptance tests (Grade 1 and 2)[S].

(编辑 刘锦伟)

Influence of jetting suction chamber on performance of centrifugal pumps

MOU Jiegang, WANG Rong, GU Yunqing, ZHENG Shuihua, LIU Fei, WANG Yang
(School of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

Taking IS100−80−160 centrifugal pump as a model-carrier, a jetting suction chamber centrifugal pump was proposed. Based on RNG k−ε turbulence model, a numerical simulation was performed for studying the internal flow under the condition of different ejector parameters, and for revealing the comprehensive influence of ejector port diameter and ejector angle on the performance of centrifugal pumps. Then the experiment was conducted to verify the correctness of numerical simulation. The results show that under the designed condition, the net positive suction head decreases first and then increases with the increase of ejector port diameter, and the head and efficiency are incremental slightly. Pressurizing effect of jetting suction chamber and centrifugal pump cavitation performance are best when the ejector port diameter is 3 mm. With the increase of ejector angle, the net positive suction head increases gradually, and the head and efficiency decrease slightly. The optimum range of ejector angle is 15°−30°. The changing trend of experimental results is consistent with numerical simulation results, which indicates the accuracy of the numerical simulation.

centrifugal pump; ejector; cavitation; numerical simulation

TH311

A

1672−7207(2016)03−0755−08

10.11817/j.issn.1672-7207.2016.03.007

2015−03−15；

2015−05−08

国家自然科学基金资助项目(51305399, 51476144)；浙江省自然科学基金资助项目(LQ15E050005) (Projects(51305399, 51476144) supported by the National Natural Science Foundation of China; Project(LQ15E050005) supported by the Zhejiang Provincial Natural Science Foundation of China)

谷云庆，博士，讲师，从事叶片泵的流场理论及减阻技术研究；E-mail: guyunqing@zjut.edu.cn