一种稀疏度自适应分段正交匹配追踪算法

唐朝伟，王雪锋，杜永光

(重庆大学 通信工程学院，重庆，400044)

一种稀疏度自适应分段正交匹配追踪算法

唐朝伟，王雪锋，杜永光

(重庆大学 通信工程学院，重庆，400044)

针对分段正交匹配追踪(StOMP)算法需要信号的稀疏度作为先验信息且重构精度较低的特点，提出一种稀疏度自适应分段正交匹配追踪算法。首先，通过对观测矩阵与初始残差相乘所得的残余相关性向量进行离散余弦变换，估算出支撑集所要扩充的最大原子数；其次，采用与抽样率成正相关的因子对较大的阈值参数进行适当修正，并对通过设定阈值所选取的原子进行优化处理；最后在StOMP算法的框架下采用变步长的方法实现稀疏度的逼近和信号的精确重构。仿真结果表明：本文所提出的算法对信号的稀疏度具有很好的自适应特性，并且在保持了较低重构复杂度的同时具有更稳定的重构质量。

压缩感知；分段正交匹配追踪；稀疏度自适应；重构性能

传统的信号采样理论Nyquist采样定理要求信号的采样频率至少为信号带宽的2倍，才能无失真地恢复原始信号。DONOHO等[1−2]提出的压缩感知理论，从信号稀疏分解和逼近角度建立了一种新的信号描述和处理的理论框架，能够在保证信息不损失的情况下，采用远低于奈奎斯特采样定理要求的速率来采样信号，即如果信号在某个变换域是稀疏的或者是可压缩的，压缩感知理论便可以利用一个与变换基不相关的观测矩阵，将变换所得的高维信号投影到一个低维空间上，根据这些少量的观测值，通过求解凸优化问题就能实现信号的精确重构。这一理论能够有效降低信号在获取、存储及传输过程中的数据量，在信号采集与处理方面带来了新的变革。重构算法是压缩感知理论中的关键问题之一，它要求在已知观测矩阵和观测向量的前提下，能高效且精确地对原始信号进行重建。目前较常用的重构算法有凸优化、组合优化和贪婪算法等，而其中的贪婪算法(通过贪婪迭代的方法来更新支撑集，并逐步逼近原始解)因其运算量小、算法简单且具有一定的重构精度而被广泛采用。贪婪算法中最早提出的有匹配追踪(matching pursuit, MP)、正交匹配追踪(orthogonal matching pursuit, OMP)[3]算法，但是这2种算法在重构效率和精度上不够理想；正则化正交匹配追踪(regularized orthogonal matching pursuit, ROMP)[4]利用正则化的方法找出候选原子集合中能量最大的原子集合来更新支撑集，压缩采样匹配追踪(compressive sampling matching pursuit, CoSaMP)[5]采用“回溯”思想来更新支撑集，这2种算法都在一定程度上提高了重构精度；分段正交匹配追踪(stagewise orthogonal matching pursuit, StOMP)[6]算法通过设定阈值进行原子的批量选取，是一种运行效率较高的重构算法，但重构精度较差；同时，上述贪婪算法均要求信号的稀疏度已知，如果对稀疏度的估计不准确，很多信号将不能得到精确重建，但是这种前提在实际应用中难以满足，稀疏度自适应匹配追踪(sparsity adaptive matching pursuit, SAMP)[7]是一种不受信号稀疏度影响的重构算法，它通过预设初始步长，并在每次迭代中增加固定的步长来逐步实现对信号稀疏度的估计，同时更新残差及支撑集以逼近原始信号，但从总体上来说该算法的重构效率较低。本文作者针对StOMP算法，提出一种稀疏度自适应且重构性能较好的改进算法，利用离散余弦变换具有能量集中的特性，估算出支撑集所要扩充的最大原子数目，并对较大的阈值参数进行修正来调节所选取的原子数目，同时对所选取的原子进行预处理并引入自适应调节步长的方法，保证用于更新支撑集原子的最佳匹配性，实现信号稀疏度的逼近和精确重构，仿真结果验证了本文所提算法在信号稀疏度自适应性和重构性能上的优越性。

1　压缩感知与StOMP算法

1.1压缩感知理论

压缩感知理论的本质是一种非适应性的、非线性的可压缩信号的重建方法，它包含3个重要的内容：信号的稀疏表示、观测矩阵测量和重构算法。

1) 信号的稀疏表示。如果长度为N的信号x∈RN在某变换域中只有K个系数不为0(或者明显大于其他系数)，且 K＜＜N，那么可以认为信号x在该变换域中是稀疏的，也可称为K-稀疏。若信号在稀疏基上的表示为S，则该稀疏变换过程可以表述如下：

3) 压缩感知算法重构。从M个测量值出发，借助观测矩阵Φ和重构算法来重建或者逼近原始信号x。在x是K-稀疏的情况下，可以把信号的重构等价于一个寻求在约束条件下的最优解问题[8−9]，表述如下：

1.2观测矩阵的选取

为了能够精确地重建稀疏或可压缩信号，对任意的K-稀疏信号x，观测矩阵Φ必须要满足限制等容特性(restricted isometry property, RIP)：

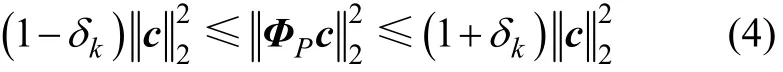
其中：ΦP为Φ中由P为索引的相关列所构成的矩阵；δk为对所有K稀疏信号满足上述特性的最小常数；c为投影到ΦP的系数序列。并且约束等距性说明Φ的行不能由Ψ的列稀疏表示，而Ψ的列也不能由Φ的行稀疏表示，即观测矩阵Φ与稀疏基Ψ不相关与约束等距性是等价的[2]，由于高斯随机矩阵与大多数由正交基构成的矩阵不相关，因此，选择高斯随机矩阵作为观测矩阵可以很好地满足RIP特性。

此外，选择对高斯随机矩阵进行正交化处理，将会使观测矩阵具有很好的去相关性[10]：

其中：Λ为特征值矩阵，是对角阵。从式(5)可以看出：信号从高维到低维投影之后的样本之间相关系数为0，即不相关，因此，在观测矩阵的选取上，正交化高斯随机矩阵是一个很好的选择。当观测矩阵Φ与稀疏基Ψ满足RIP准则时，在观测过程中能够保 证信号的重要信息不丢失，这将有助于信号的精确重建。

1.3分段正交匹配追踪(StOMP)算法

对于压缩感知中的正交匹配追踪算法而言，它每次从观测矩阵中仅选取1个最佳原子，虽然这种方式在一定程度上保证了图像重构的精确度，但不可避免地造成该算法在整个原子选取的过程中，因匹配次数太多而增大计算量并最终降低整个重构过程的效率。而StOMP算法本质就在于每次匹配时选出的并不是1个原子，而是通过设定阈值选取多个原子，形成1个初始的原子集合，然后更新支撑集，并利用最小二乘法求得近似解，同时完成对残差的更新，最后来检查是否满足终止条件，若不满足，则以更新的残差继续进行原子的匹配追踪，从而大大减少匹配次数，提高重构效率。

StOMP算法步骤：

StOMP算法在选取原子时进行了一定程度的简化，提高了算法执行速度，但它也有自身的不足：1) 由于其在每次迭代的过程中寻找的都不是信号最佳匹配原子，因此导致信号的重构精度低于OMP算法的重构精度，重构的稳定性也不能得到保证[11]；2) 该算法通过设定阈值ts=θδs每次选取多个原子更新支撑集，但在实际操作中，阈值参数θ的选择较难[11]；3) 需要指出的是StOMP算法需要信号的稀疏度作为先验知识，只有正确估计了信号的稀疏度，才能精确地重构原始信号。然而，对于实际信号(如语音和图像在其稀疏域上仅是近似稀疏的)，难以准确估计其稀疏度。

2　稀疏度自适应StOMP算法

针对上述StOMP算法的不足，本文在深入研究离散余弦变换(discrete cosine transform, DCT)变换的特点、阈值参数对原子选取的影响和稀疏度自适应算法[12−13]的基础上，提出了一种具有稀疏度自适应且重构性能较好的算法。其主要思想是：首先对观测矩阵与初始残差相乘所得的残余相关性向量进行DCT变换，估算出支撑集所要扩充的最大原子数；然后，采用一个与抽样率成正相关的因子对较大阈值参数进行修正，并对通过设定阈值所选取的原子进行优化排序，再比较原子集合内原子的数目和此时的步长，确定所要选取的原子数目，更新支撑集；最后在StOMP算法框架下，不断更新步长和扩充支撑集，在逐步逼近信号稀疏度的同时获得信号的精确重构。以下从支撑集最大原子数目估计及原子预处理、阈值参数修正、稀疏度自适应和算法步骤等4个方面对稀疏度自适应StOMP算法进行描述。

2.1支撑集最大原子数目估计及原子预处理

2.1.1支撑集最大原子数目估计

在图像视频编码中，经常采用DCT或者基于DCT的变换(如H.264的整数变换)来提高编码效率，同时取DCT变换之后的局部DCT系数进行反变换或者对DCT系数的局部测量值进行压缩感知重构，通常能以极大的概率来恢复原始数据[14]。重构算法中，需要从观测矩阵Φ和M维观测向量y出发，得到1个N维的重构向量。在本文中利用DCT变换来估计支撑集最大原子数目：首先，观测矩阵与该观测向量(初始残差)相乘得到残余相关性向量；然后对向量VCR进行DCT变换，将所得向量中的元素按绝对值大小进行排序，并把该向量最后M个数值较小的系数置0，利用离散余弦变换较强的能量集中特性，找出最能代表该向量能量的一批原子 (在该算法中，所选取原子的能量占原子总能量的90%)，并设定这批原子的数目为支撑集所要扩充的最大数目Lmax。

2.1.2原子预处理

通过设定阈值，每次迭代时都将选取一批原子，定义观测矩阵Φ与更新残差rs的内积为Cs，即，那么这些原子就是Cs中大于阈值的数值对应的索引值所形成的候选集。在本文中对候选集中的原子做一定的处理：首先，找出候选集中的原子对应在向量Cs中的数值，然后对这些数值进行降序排列，并依次返回这些数值对应在向量Cs中的位置，形成新的候选集，此时该候选集中的第1个索引值就对应向量Cs中的最大值，即该索引值为最优匹配原子，第2个索引值为次优匹配原子。这样，在算法进程中，总能优先选出最为匹配的一些原子来扩充支撑集。

2.2阈值参数修正

选取Lena和Boat 2幅标准测试图像，设定不同的抽样率r，测试StOMP算法在不同阈值参数θ下重构图像的峰值信噪比(peak signal to noise ratio，PSNR)，结果分别如表1和表2所示。

由表1和表2可知：对于Lena和Boat 2幅图像，在抽样率相对较低的条件下，当阈值参数较低时，由于筛选出的候选集原子较多，造成过度估计而影响重建效果，从而峰值信噪比较低；当阈值参数过高时，由于筛选出的候选集原子数较少而降低了重建质量，峰值信噪比也较低。因此，阈值参数的选取对图像的重建效果有着很大的影响。

图像处理中，低抽样率具有较好的实用意义，而且，当阈值参数较大时(θ取值范围为[2.6,3])，StOMP算法因候选集选取的原子较少而具有更高的重构效率，但图像的重构质量不佳。因此，综合考虑重构效率与重构精度，当阈值参数较大时，可以适当修正阈值参数[15−16]，本文通过一个与抽样率成正相关的因子来调节阈值参数，即(本文采用的修正因子为)，通过适当降低阈值参数来增加候选集原子数，达到提升重建精度的目的。

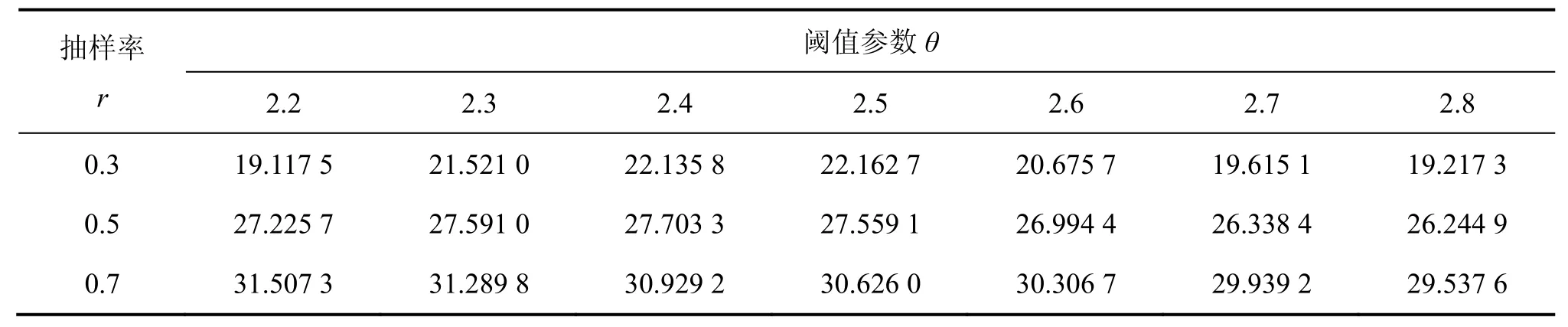
表1　不同阈值参数下Lena重构图像的峰值信噪比Table 1 PSNR of reconstructed Lena image with different threshold parameters　dB

表2　不同阈值参数下Boat重构图像的峰值信噪比Table 2 PSNR of reconstructed Boat image with different threshold parameter　dB

2.3稀疏度自适应

在信号稀疏度未知的情况下，本文算法将迭代过程分为若干个阶段，在每个阶段均进行步长的调整，并根据步长实现对候选集中原子的阶段性选取[17−18]，随着迭代过程的分段进行，步长不断地更新，稀疏度的近似估计和支撑集的扩充也同步进行。首先，设定初始步长；然后通过设定阈值形成原子候选集，经过原子预处理之后，对此时候选集内的原子数目与当前步长进行判定，如果候选集内原子数目大于步长Ls，那么仅选取候选集中前Ls个索引值用于扩充支撑集，否则全部用于支撑集的扩充，随着重构过程的进行，逐步对步长进行更新，并完成稀疏度的近似估计，此时支撑集得到了有效扩充，能够用于信号的精确重构。

增设算法的终止条件为支撑集内的原子数目达到一定的数量Lmax，这样在保证用于重构信号时有一定的原子数目，提高重构精度的同时，也在一定程度上弥补了当信号稀疏度较大时，会因迭代次数较多导致运算量过大的不足，即在原子数目达到一定数量后，算法不再进行迭代运算，从而保证了算法的重构效率。

2.4算法步骤及分析

算法中步骤1)～3)通过对残余相关性向量的DCT变换处理，估计了迭代中支撑集所要扩充的最大原子数目，步骤4)通过设定阈值来选取一部分原子形成候选集，通过步骤5)的原子预处理，使候选集的索引值顺序对应内积Cs中从大到小的数值，从而保证在步骤6)中总能优先选出最为匹配的一些原子来扩充支撑集Is，步骤6)和7)实现了利用最小二乘法逼近原始信号和余量的更新，在步骤8)中，首先检查算法是否终止，否则进入下一阶段并更新步长后转入步骤4)。

3　实验结果及分析

本文实验中，稀疏变换采用离散小波变换DWT (discrete wavelet transform)；观测矩阵为高斯随机矩阵(gaussian random matrix，GRM)和正交化高斯随机矩阵(orthogonalized gaussian random matrix，OGRM)，具体使用将在各部分实验中作出说明；对于本文的仿真结果，采用主客观相结合的标准进行评价：对各算法的重构图像进行主观评价，用峰值信噪比(dB)来客观评价各种算法的重构质量，用重构时间(s)来客观评价各种算法的重构复杂度；各算法的峰值信噪比和运行时间均为200次实验的平均结果。本实验在酷睿双核2.20 GHz，2 GB内存的PC机上，通过MATLAB R2010a仿真完成。

3.1不同阈值参数条件下信号重构性能仿真及分析

本节实验采用大小为256×256的Lena图像、512×384的Peppers图像、346×207的Canoe图像和240×320的Football图像作测试，观测矩阵分别采用高斯随机矩阵(GRM)和正交化高斯随机矩阵(OGRM)，取固定的抽样率r=0.5，阈值参数θ取值范围为[1,3]，其他条件保持一致，在不同阈值参数条件下，StOMP和本文算法对四幅图像的重构曲线如图1所示。

由图1可知：对于4幅测试图像，当观测矩阵为高斯随机矩阵时，StOMP算法在阈值参数为[2, 3]时具有较好的重构效果；当观测矩阵为正交化高斯随机矩阵时，StOMP算法在阈值参数为[1.6, 2.4]时具有较好的重构效果。而本文提出的算法，选取相同的观测矩阵时，在不同阈值参数条件下均比StOMP算法具有更好地重构效果，且重构效果较为稳定。因此，本文所提出的算法在阈值参数的选取上会具有更大的灵活性，能更好地应用于图像处理领域。

3.2不同稀疏度条件下信号重构性能仿真及分析

本节实验比较MP，OMP，CoSaMP，SAMP，StOMP和本文算法在不同稀疏度条件下的正确重构概率和重构时间。采用长度为N=256的高斯稀疏信号，测量数目M=128，K的取值范围为[1, 80]。在本部分实验中，当观测矩阵为高斯随机矩阵时，StOMP和本文算法的阈值参数取值范围选择[2, 3]；当观测矩阵为正交化高斯随机矩阵时，2种算法的阈值参数取值范围选择[1.6, 2.4]，2种情况下各取10个阈值参数，以不同阈值参数下的正确重构概率的平均值作为该算法的正确重构概率。定义信号正确重构的原则是重构信号与原始信号x中的非零元素的位置相同，并且残差能量小于一定阈值，取。实验中MP， OMP和StOMP算法的实现采用的是Sparselab工具箱，CoSaMP和SAMP算法参考的是Compressive Sensing Resources程序包。观测矩阵为高斯随机矩阵和正交化高斯随机矩阵时，各算法在不同的稀疏度下的重构性能见图2和图3。

由图2(a)可知：当观测矩阵为高斯随机矩阵时，本文算法的正确重构率高于MP，OMP，CoSaMP和StOMP等算法，在一定程度上低于SAMP算法；图3(a)表明：当观测矩阵为正交化高斯随机矩阵时，本文算法比MP，OMP，CoSaMP和StOMP算法具有更高的正确重构率，与SAMP算法的重构精度相当，只是在稀疏度大于0.25时才会有较多的信息不能够正确重构。由图2(b)和3(b)可知：采用不同的观测矩阵时，本文算法通过设置最大扩充原子数目，相比于SAMP算法而言，避免了过多的迭代计算，运行效率远高于SAMP算法，与StOMP算法重构效率相当。可见，本文所提出的算法提高了稀疏度较大时的信号正确重构率，尤其是采用正交化高斯随机矩阵作为观测矩阵时，具有更好的稀疏度自适应性。

图1　不同阈值参数下StOMP和本文算法的重构曲线Fig. 1 Reconstruction curve of StOMP and the proposed algorithm with different threshold parameters

图2　各算法基于高斯随机观测矩阵在不同稀疏度下的重构性能Fig. 2 Reconstruction performance of algorithms with different sparsity when sensing matrix is GRM

3.3算法在图像处理中的应用

本节实验验证MP，OMP，CoSaMP，SAMP，StOMP和本文算法等在图像处理中的实用性。测试图像选择Lena图像，其中SAMP和本文算法的初始步长取值均为Ls=9，StOMP和本文算法的阈值参数均取θ=2，观测矩阵均采用正交化高斯随机矩阵，抽样率取值分别为0.4，0.5和0.6，其他条件均保持一致，图4所示为抽样率r=0.5时各算法的重构图像，表3所示为不同抽样率下各算法的重构性能。

由图4可知：本文算法和SAMP算法具有较好的图像重构效果。由表3可知，从重构峰值信噪比的角度来看，在相同的抽样率下，SAMP和本文算法的峰值信噪比要明显高于其他几种算法，其中，在r=0.5时，本文算法的PSNR比StOMP算法的峰值信噪比高1.2 dB左右，与SAMP算法重构精度相当，这主要归因于用于更新支撑集的原子都是最为匹配的，即本文算法能获得比StOMP算法更好的图像重构效果。从运行效率的角度来看，在相同的抽样率下，StOMP和本文算法的重构时间要小于其他几种算法的重构时间，其中，本文算法的重构时间要远远小于SAMP算法的重构时间，这主要归因于支撑集最大扩充原子数目的估计，相较于SAMP算法，受到步长的影响较小，且本文算法的重构时间略大于StOMP算法的重构时间，即本文算法保持了StOMP算法重构复杂度较低的优点。综合来说，本文所提出的算法在保持了原算法较高运行效率的同时，具有了更好的图像重构精度，在图像处理领域中会具有很好的实用意义。

图3　各算法基于正交化高斯随机观测矩阵在不同稀疏度下的重构性能Fig. 3 Reconstruction performance of algorithms with different sparsity when sensing matrix is OGRM

表3　不同抽样率下各算法的重构性能对比Table 3 Performance comparison of the algorithms with different sampling rate

图4　相同抽样率r=0.5时各算法的重构图像Fig. 4 Reconstructed image of algorithms with the same sampling rate (r=0.5)

4　结论

1) 提出了一种稀疏度自适应且重构性能较好的StOMP算法，该算法首先估计出每次迭代时支撑集所要扩充的最大原子数，在一定程度上保证了算法的重构效率；然后对较大的阈值参数通过一个与抽样率成正相关的因子进行修正，同时对设定阈值所选取的原子进行优化处理，保证了用于更新支撑集的均为最佳匹配的候选原子；最后根据当前步长来选取一定数目的原子更新支撑集，在逐步调整步长的同时实现稀疏度的逼近和信号的精确重构。

2) 该算法大大提高了信号稀疏度较大时的正确重构率，具有较好的稀疏度自适应性，并能很好地兼顾图像重构的效率和精度，在图像处理领域具有很好的实际应用价值。

[1] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289−1306.

[2] CANDÈS E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21−30.

[3] TROPP J A, GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655−4666.

[4] NEEDELL D, VERSHYNIN R. Signal recovery from inaccurate and incomplete measurements via regularized orthogonal matching pursuit[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 310−316.

[5] NEEDELL D, TROPP J A. CoSaMP: iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301−321.

[6] DONOHO D L, TSAIG Y, DRORI I, et al. Sparse solution of underdetermined linear equations by stagewise orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2012, 58(2): 1094−1121.

[7] DO T T, GAN L, NGUYEN N, et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]// Proceedings of the Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA: IEEE Computer Society, 2008: 581−587.

[8] 杨海蓉, 张成, 丁大为, 等. 压缩传感理论与重构算[J]. 电子学报, 2011, 39(1): 142−148.YANG Hairong, ZHANG Cheng, DING Dawei, et al. Theory of compressed sensing and reconstruction algorithm[J]. Acta Electronica Sinica, 2011, 39(1): 142−148.

[9] BARANIUK R. Compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118−121.

[10] 苏雅茹. 高维数据的维数约简算法研究[D]. 合肥: 中国科学技术大学自动化学院, 2012: 36−39. SU Yaru. Research on dimensionality reduction of high-dimensional data[D]. Hefei: University of Science and Technology of China. College of Automation, 2012: 36−39.

[11] 方红, 杨海蓉. 贪婪算法与压缩感知理论[J]. 自动化学报, 2011, 37(12): 1413−1421. FANG Hong, YANG Hairong. Greedy algorithm and compressed sensing theory[J]. Journal of Automation, 2011, 37(12): 1413−1421.

[12] 王良君, 石光明, 李甫, 等. 混合观测压缩感知图像多描述编码[J]. 光学精密工程, 2013, 21(3): 724−733. WANG Liangjun, SHI Guangming, LI Fu, et al. Compressive sensing multiple description image coding with hybrid sampling[J]. Optics and Precision Engineering, 2013, 21(3): 724−733.

[13] CORMODE G, MUTHUKRISHNAN S. Combinatorial algorithms for compressed sensing[C]// Proceedings of the 40th International Conference on Information Science and Systems. Princeton, NJ: IEEE, 2006: 280−294.

[14] 潘榕, 刘昱, 侯正信, 等. 基于局部DCT系数的图像压缩感知编码与重构[J]. 自动化学报, 2011, 37(6): 674−681. PAN Rong, LIU Yu, HOU Zhengxin, et al. Image coding and reconstruction via compressed sensing based on partial DCT coefficients[J]. Journal of Automation, 2011, 37(6): 674−681.

[15] BLUMENSATH T, DAVIES M. Iterative hard threshold for compressed sensing[J]. Applied and Computational Harmonic Analysis, 2009, 27(3): 265−274.

[16] BECK A, TEBOULLE M. A fast iterative shrinkagethresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183−202.

[17] 高睿, 赵瑞珍, 胡绍海. 基于压缩感知的变步长自适应匹配追踪重建算法[J]. 光学学报, 2010, 30(6): 1639−1644. GAO Rui, ZHAO Ruizhen, HU Shaohai. Variable step size adaptive matching pursuit algorithm for image reconstruction based on compressive sensing[J]. Acta Optical Sinica, 2010, 30(6): 1639−1644.

[18] 杨成, 冯巍, 冯辉, 等. 一种压缩采样中的稀疏度自适应子空间追踪算法[J]. 电子学报, 2010, 38(4): 1914−1917. YANG Cheng, FENG Wei, FENG Hui, et al. A sparsity subspace pursuit algorithm for compressive sampling[J]. Acta Electronoca Sinica, 2010, 38(4): 1914−1917.

(编辑 赵俊)

A sparsity adaptive stagewise orthogonal matching pursuit algorithm

TANG Chaowei, WANG Xuefeng, DU Yongguang
(College of Communication Engineering, Chongqing University, Chongqing 400044, China)

An improved stagewise orthogonal matching pursuit (StOMP) algorithm was proposed considering that the algorithm needs signal sparsity as the prior knowledge and has a relatively poorer reconstruction performance. Firstly, discreet cosine transform was applied to the vector of residual correlations to estimate the maximum number of atom needed by the support set. Then the large threshold parameter was adjusted by a factor which is positively correlated with the sampling rate and the atoms chosen by setting a threshold value was optimized. Finally, the close approach of signal sparsity and precise reconstruction of the signal were realized with variable step size within the frame of StOMP. The results show that the proposed algorithm has good adaptability without prior information of the sparsity and this algorithm not only keeps the low reconstruction complexity but also shows better and more stable reconstruction quality than the original StOMP algorithm.

compressive sensing; stagewise orthogonal matching pursuit; sparsity adaptive; reconstruction performance

TN911.7

A

1672−7207(2016)03−0784−09

10.11817/j.issn.1672-7207.2016.03.011

2015−03−28；

2015−05−06

国家科技重大专项项目(2010ZX03004-002-01) (Project(2010ZX03004-002-01) supported by the National Science and Technology Major Program of China)

唐朝伟，博士(后)，教授，从事宽带无线移动多媒体、智能信息处理等方面的研究；E-mail: cwtang@cqu.edu.cn