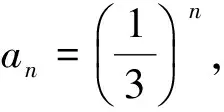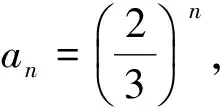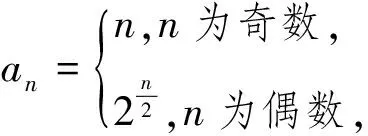等比数列背景下的一类不定方程问题

江苏省海门中学 (226100) 张庆秋

等比数列背景下的一类不定方程问题

江苏省海门中学 (226100) 张庆秋

数列中的不定方程问题，是近年来高考的一个热门问题，其类型及处理方法也是多种多样，如利用整除性、奇数与偶数、整数与小数、范围等等．本文就等比数列背景下的一类问题，谈谈其基本的处理方法．

问题1 已知等比数列{an}的通项公式为an=2n，试问：数列{an}中是否存在不同的三项使其成等差数列？若存在，请求出该项；若不存在，请说明理由．

解：假设存在不同三项ar,as,at(其中r

又r-s<0,t-s>0，且r-s∈Z,t-s∈Z，易知(*)式左边是整数，右边不是整数，故(*)式不成立，与假设矛盾．

因此，数列{an}中不存在不同的三项使其成等差数列．

又r-s<0,t-s>0，且r-s∈Z,t-s∈Z，易知(*)式左边是整数，右边不是整数，故(*)式不成立，与假设矛盾．

因此，数列{an}中不存在不同的三项使其成等差数列．

因此，数列{an}中不存在不同的三项使其成等差数列．

注意到以上三个不定方程的处理，均利用了在其等式两边同时乘以或者除以与公比相关的一个数，达到整数与小数不相等的效果(也可以通过适当调整结合整数的整除性)，从而产生矛盾．事实上，对于任意公比为有理数(不为±1)的等比数列，均不存在不同的三项使其成等差数列．

又r-s<0,t-s>0，且r-s∈Z,t-s∈Z，易知(*)式左边是整数，右边不是整数，故(*)式不成立，与假设矛盾．

因此，数列{an}中不存在不同的三项使其成等差数列．

利用上述结论能够很快解决一些以其为背景的问题，如：

分析：数列{an}中的奇数项为奇数，偶数项为偶数，故最终形成的等差数列必为{an}中的奇数项和偶数项交叉排列而成．

由问题1及其变式1、2的结论可知，偶数项至多两项(否则将这些偶数项取出，亦成等差数列，矛盾)，从而奇数项至多三项．

因此数列{an}中最多能找到不同的五项，按照某种顺序排列使其成等差数列，如1，2，3，4，5．

除了直接运用上述结论之外，其蕴含的处理方法在一些以等比数列为背景的不定方程问题中同样有着广泛的应用，如：

问题3 已知等比数列{an}的通项公式为an=2n，试问数列{an}中是否存在某一项，它可以表示为该数列中其它r(r∈N,r≥2)项的和？若存在，请求出该项；若不存在，请说明理由．

解法1：假设存在as，使得as=at1+at2+…+atr(其中t1

又s-t2>0,t1-t2<0,t2-t2=0,…,tr-t2>0，且s-t2,t1-t2,t2-t2,…,tr-t2∈Z，易知(*)式左边是整数，右边不是整数，故(*)式不成立，与假设矛盾．

因此，数列{an}中不存在某一项，它可以表示为该数列中其它r(r∈N,r≥2)项的和．

解法2：假设存在as，使得as=at1+at2+…+atr，(其中t1

因此，数列{an}中不存在某一项，它可以表示为该数列中其它r(r∈N,r≥2)项的和．