解决恒成立问题的基本策略
四川 李 华
(作者单位:四川省渠县第二中学)
解决恒成立问题的基本策略

恒成立问题是高考的必考内容,它常常与一元二次不等式、函数的最值、函数的图象、任意性存在性等知识联系起来,也是函数中的重要内容,其涉及的思想方法常有分类讨论、变量分离、图象分析等,本文就高考问题中常用的一些基本策略进行研究,旨在利于高三师生复习参考.
一、一元二次不等式在某区间上恒成立
【例1】关于x的不等式ax2-2ax+1≥0在[2,4]上恒成立,求实数a的取值范围.
【解析】当a=0时,符合题意;当a≠0时,设函数f(x)=ax2-2ax+1,对称轴为x=1;
当a>0时,开口向上,函数f(x)在[2,4]上单调递增,只需f(x)min=f(2)≥0即可,此时解得a>0;


【变式】已知关于x的不等式x2-2ax+1>0在(2,4)上恒成立,求实数a的取值范围.
二、图解法处理不等式恒成立问题
【例2】若关于x的不等式|a|<|x+1|+|x-2|解集是R,则实数a的取值范围是________.


【评注】对于不等式恒成立,其相应的函数的最值求解是关键,其中图解法求最值就是其中一种重要的策略.通过作出相应函数的图象,可以获得函数的最大值或最小值,进而得到字母参数应该满足的条件.
三、用图形的覆盖问题处理不等式f(x)≤g(x)恒成立


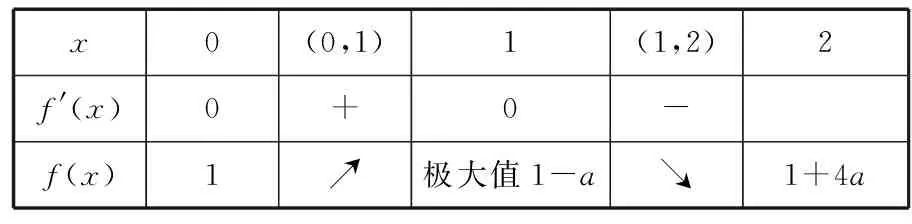
【评注】用数形结合法解决含参不等式恒成立问题需“两招”,第一招:转化和化归,即把“f(x) 【例4】当x∈[-2,1]时, 不等式ax3-x2+4x+3≥0恒成立,求实数a的取值范围. 【解析】①当x=0时,0≥-3,故实数a的取值范围是R; 故函数f(x)递增,则f(x)max=f(1)=-6, 故a≥-6; 易知f(x)min=f(-1)=-2,则a≤-2. 综上所述,实数a的取值范围是[-6,-2]. 【评注】一般地,恒成立的不等式可以将字母单独分离,从而转化成a≤f(x),a≥f(x),a 【变式】当x∈[-2,1]时, 不等式ax3-x2+4x+3≥0恒成立,求实数a的取值范围. 【解析】①当x=0时,0≥-3, 故实数a的取值范围是R; 故函数f(x)单调递增,则f(x)max=f(1)=-6, 故a≥-6; 易知f(x)min=f(-1)=-2,则a≤-2. 综上所述,实数a的取值范围是[-6,-2]. 【例5】已知函数f(x)=x2-2x+1和g(x)=x3-3x2-6x+m,若任意x1,x2满足x1∈[-2,2],x2∈[-2,2],都有f(x1)≤g(x2),求m的取值范围. 【评注】不等式f(x1)≤g(x2)恒成立,可以理解为定义域均为[-2,2]时,函数f(x)中的最大值不超过g(x)的最小值.通过条形图来理解位置的高低变化,可以形象地解决任何双变量问题,字母取值范围必然涉及区间的开与闭,起决定因素的是不等号以及函数最值的存在性.比如a 【解析】由题意,f′(x)=6ax2-6ax=6ax(x-1),a<0,故有 x0(0,1)1(1,2)2f'(x)0+0-f(x)1↗极大值1-a↘1+4a 【例6】已知不等式mx2-2x-m+1<0. (1) 是否存在m对所有的实数x,使不等式恒成立,若存在,求出m的取值范围; (2)设不等式对于满足|m|≤2的一切m的值都成立,求符合题意的x的取值集合. 【评注】常见的恒成立问题都是“主元x在某个区间上不等式恒成立,求字母的范围”,但是上述问题是“已知字母范围,求的是主元x的范围”.此类问题,我们只需要变换一个角度,把字母看成是主元就行了.这就是变换主元法. 【变式】若任意a∈[1,3],使得不等式ax2+(a-2)x-2≤0恒成立,则实数x取值范围是________. (作者单位:四川省渠县第二中学)
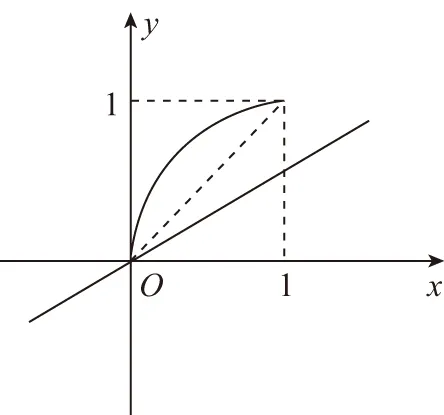
四、分离变量法研究不等式恒成立问题
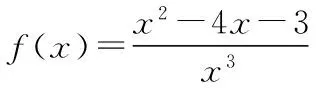


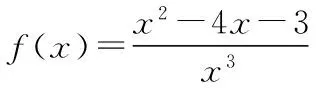


五、对任意性、存在性单变量或双变量恒成立问题用最值研究


六、变换主元法处理不等式恒成立问题



七、控制变量法研究多变量型问题