涉及多个三角形的解三角形问题

湖南 王 勇

(作者单位：湖南省郴州二中)

涉及多个三角形的解三角形问题

解三角形是高中数学的重点内容，是高考数学的热点问题.这类题目有时会涉及多个三角形、四边形甚至多边形.往往有一定的难度.现就这类问题总结一些常用的解题策略，供同学们参考.

1．构造辅助高线，化斜为直

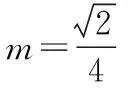
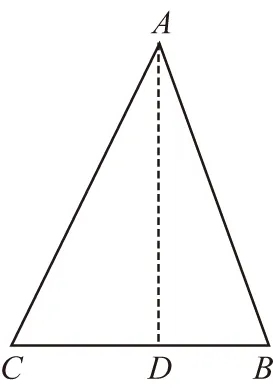
【评注】作高构造直角三角形，可以把斜三角形问题转化直角三角形问题.特别是题设条件涉及角的正切值时，常常作高构造直角三角形，将这些角作为直角三角形的锐角，简化解题过程.

【变式1】如图，两座相距60 m的建筑物AB，CD的高度分别为20 m，50 m，BD为水平面，则从建筑物AB的顶端A看建筑物CD的张角为________.

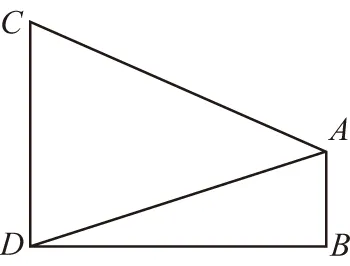
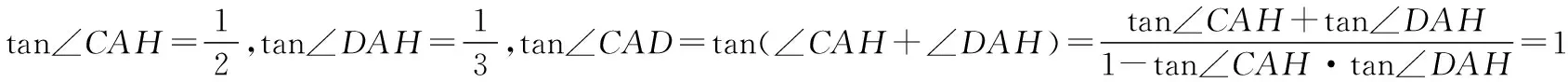
又0°<∠CAD<180°，所以∠CAD=45°，

所以从建筑物AB的顶端A看建筑物CD的张角为45°.

2.利用相邻补角互补，建立联系

【例2】在△ABC中，BC边上的中线为AD，求证:AB2+AC2=2AD2+2BD2.

【证明】如图，易知cos∠ADB=-cos∠ADC，

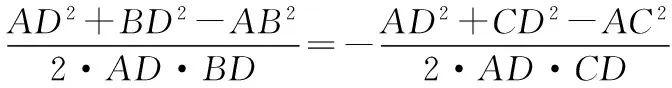
又BD=CD，

化简即得AB2+AC2=2AD2+2BD2.

【评注】借助三角形中线分割成的两个邻补角的余弦互为相反数，在两个三角形中分别使用余弦定理，可以得到中线长与三角形三边的数量关系;同样，平行四边形两条对角线的平方和等于其四边的平方和.

【变式】在△ABC中，AB=2,AC=3，BC边上的中线AD=2，求△ABC的面积S.

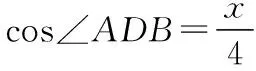
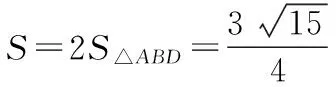
3. 利用角平分线构造等角关系，进行等量转换

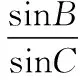
【变式】在△ABC中，AB=2,AC=1，∠A的平分线AD=1，求△ABC的面积S.

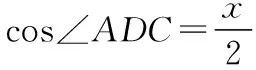
4.多次使用正、余弦定理，先定性分析再定量计算

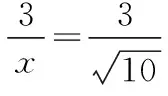
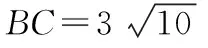
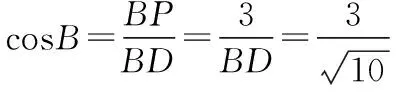
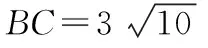
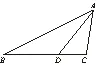
设AD=x，则在△ABD中，由余弦定理得

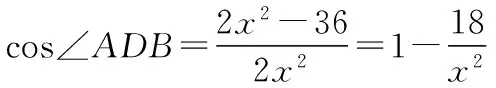
又cos∠ADC=-cos∠ADB，

【评注】多次使用正、余弦定理是图形类问题的常见策略.在解题过程中，应结合条件，画出正确示意图，分析已知和所求之间的联系，然后再在相应的三角形中逐步利用正、余弦定理计算.不同的解题思路,选择的三角形先后顺序往往不同，可以得到不同的解题过程.

又cos∠ADB=-cos∠ADC，解得x=1，故AC=1.

所以1-4x2=-1-2x2，解得x=1，故AC=1.

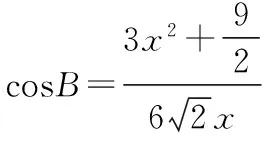
所以，∠B=135°，解得x=1，故AC=1.

5.连接对角线，将四边形切割为多个三角形

【例5】如图，四边形AOCB中，OA⊥OC,CA⊥CB,AC=2,CB=1，则OB的长度的取值范围是________.

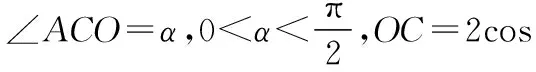
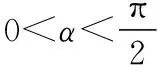
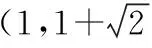
【评注】四边形可以分割为多个三角形，例如，本例题就将四边形AOCB进行了分割，根据已知条件，在△AOC和△OBC中利用有关定理，就可以将OB表示出来.

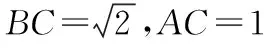
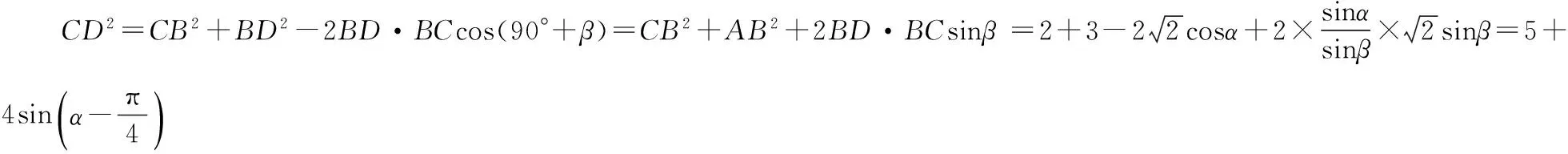
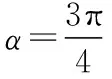
6.应用四边形对角互补，建立解题桥梁

【例6】A,B,C,D为平面四边形ABCD的四个内角.

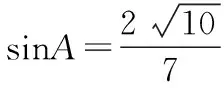
因为A+C=180°，所以由(Ⅰ)得

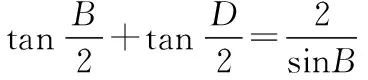
【评注】△ACB与△ACD有一条公共边，且B+D=180°，则有cosD=-cosB.以此为桥梁，分别在两个三角形中利用余弦定理，就能建立关于角B或角D的等式，于是角B或角D就可求.

【变式】如图四边形ABCD的内角A与C互补，AB=1，BC=3，CD=DA=2.

(Ⅰ)求角C的大小和BD的长；

(Ⅱ) 求四边形ABCD的面积.

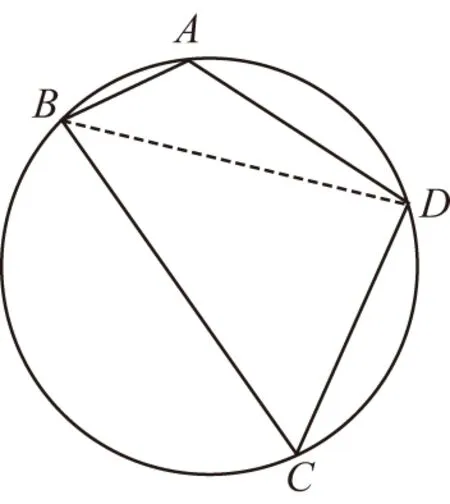
【解析】(Ⅰ)连接BD，在△ABD中，由余弦定理得BD2=AB2+AD2-2AB·ADcosA；在△BCD中，由余弦定理得BD2=BC2+CD2-2BC·CDcosC.又cosA+cosC=0，

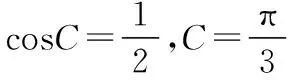
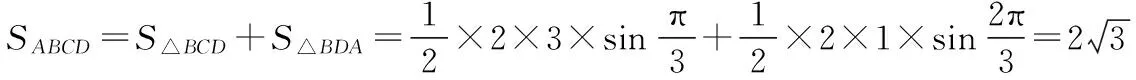
(作者单位：湖南省郴州二中)