并列问题递进解:难题思路获取的“暗示”
——以两道模考综合题为例
☉江苏苏州工业园区青剑湖学校 丁志国
并列问题递进解:难题思路获取的“暗示”
——以两道模考综合题为例
☉江苏苏州工业园区青剑湖学校 丁志国
中考综合题通常下设2~3问,从目前“流行”的命题趋势来看,以并列式问题为多,即各个小问之间互相独立,条件不能交叉混用,但是有些优秀的试题虽然各个小问之间的条件不能混淆,它们背后的解法思路却体现着并列式问题与递进式求解,也就是当后一问较难试题的思路受阻时,要善于退回上一问,思考上一问解法的启示,或上一问解题成果的扩大,这时往往“柳暗花明”,获得思路的贯通.本文就最近解题教学期间收集到的一些优秀模考题,讲解这种解答策略,并跟进教学思考,供研讨.
一、考题及思路突破
考题1:已知抛物线C:y=(x+2)[t(x+1)-(x+3)],其中-7≤t≤-2,且无论t取任何符合条件的实数,点A、P都在抛物线C上.
(1)当t=-5时,求抛物线C的对称轴;
(2)当-60≤n≤-30时,判断点(1,n)是否在抛物线C上,并说明理由;
(3)如图1,若点A在x轴上,过点A作线段AP的垂线交y轴于点B,交抛物线C于点D,当点D的纵坐标为时,求S△PAD的最小值.
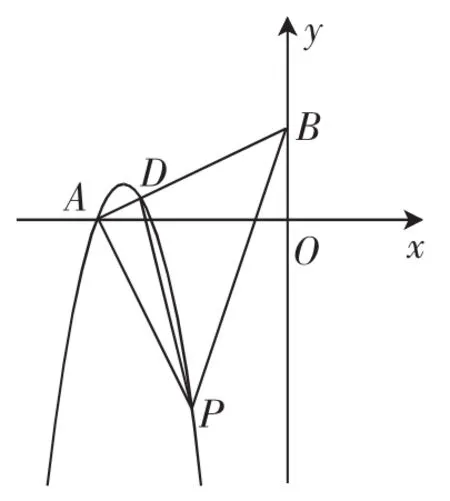
图1
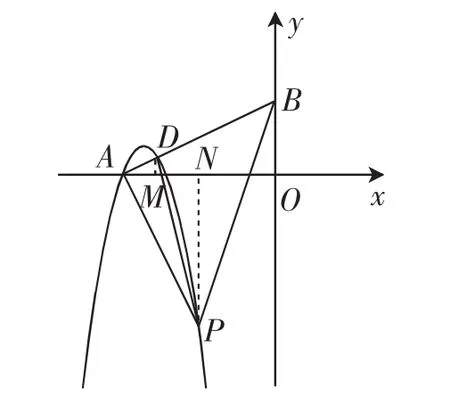
图2
思路讲解:(1)把t=-5代入抛物线C的解析式中,整理得y=-6x2-20x-16,结合对称轴方程,即得对称轴为直线
(2)若(1,n)在抛物线上,将点(1,n)代入解析式,得n=6t-12.结合题干条件-7≤t≤-2,可以分析出-54≤n≤-24.比对另一个n的取值范围-60≤n≤-30,只有在它们的公共部分“-54≤n≤-30”,点(1,n)在抛物线C上;而当-60≤n<-54时,点(1,n)不在抛物线C上.这里解答时要注意分类讨论.
(3)这道较难题的起点在于确认点A、P的坐标,信息在题干中,一直没有使用(前两问并没有涉及这个信息,闲置一段时间后,容易忽略).由点A在x轴上,抛物线C的解析式“y=(x+2)[t(x+1)-(x+3)]”的特点,容易看出可能是x+2=0,此时对应着A(-2,0),另一个点P的坐标稍难,让我们把目光投向解析式中的“[t(x+1)-(x+3)]”,要使这个式子的值与t无关,则x=-1,即此时P(-1,-2).
如图2,过点P作PN⊥x轴于点N,可得PN=AO=2,∠PNA=∠AOB=90°.由PA⊥AB,得∠PAN+∠BAO=90°.又∠ABO+∠BAO=90°,所以∠PAN=∠ABO.于是△PAN≌△ABO.可得BO=1,再由勾股定理得
过点D作DM⊥x轴于点M,可得∠DMA=∠BOA=90°.又∠DAM=∠BAO,所以△DAM∽△BAO,得比例式.所以(注意,这里也可以根据锐角三角函数快速得出)所以由A(-2,0)、B(0,1),解读出直线AB的解析式为1.当时,x=2m-1(.这里点D的坐标,也可以根据AM、MO的长演算得出)把点代入抛物线C的解析式,得
另解思考:确认点A、P、B的坐标之后,可写出直线AB的解析式为将其与抛物线C的解析式联立,得
回顾反思:这道试题第(1)问是送分题,但是第(2)问就需要较为扎实的运算、变形能力,且运算到n的取值范围之后需要与另一个范围比对、确认公共部分,并分类讨论获得解集.重要的是,第(2)问的解题思路将启示第(3)问中关于m取值范围的确定,成为解题过程中一个关键步骤.这种解题策略,我们可称之为“并列式问题与递进式求解”.以下我们再选取一道体现类似解答策略的几何考题,进一步讲解.
考题2:在△ABC中,D为BC边上一点.
(1)如图3,在Rt△ABC中,∠C=90°,将△ABC沿着AD折叠,点C落在AB边上.请用直尺和圆规作出点D(不写作法,保留作图痕迹).

图3

图4
(2)如图4,将△ABC沿着过点D的直线折叠,点C落在AB边上的E处.
①若DE⊥AB,垂足为E,请用直尺和圆规作出点D(不写作法,保留作图痕迹);
②若AB=4 ■ 2,BC=6,∠B=45°,求CD的取值范围.
思路讲解:第(1)问属于基本作图,理解题意后知道应该作出∠A的角平分线.
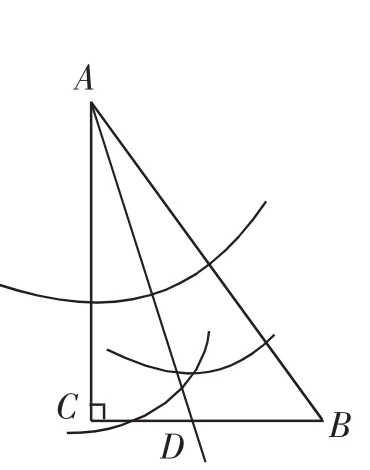
图5
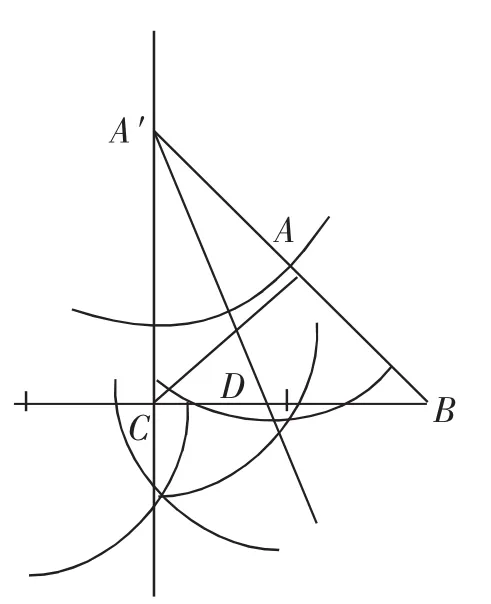
图6
第(2)①问需要分析出考查意图,可利用草图分析,确认应该“转向”第(1)问的基本图形,构造出一个直角三角形A′BC,再作出∠BA′C的角平分线交BC于点D.
对于第(3)②问,先构思图7.
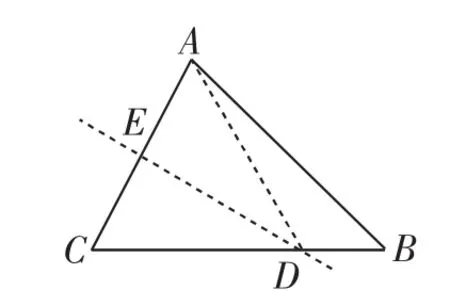
图7
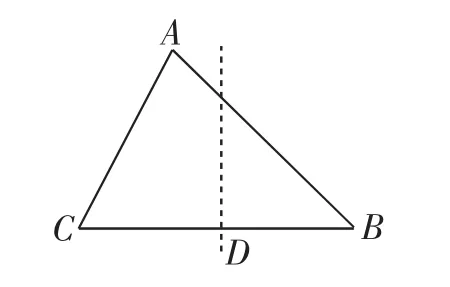
图8
作出AC的垂直平分线交BC于D点,结合已知线段的长及∠B是45°,可以确认CD=5,这也就是CD的最大值,此时C点的对称点落在点A处;最小值比较复杂,一个易错点是想象成点C与B互为对称点,从而得到CD=3;这时如果“到此为止”,缺少对图6的这种情形进行分析,则解答并不完善.让我们把目光投向上一问中的图6,可以确定,比较一下与3的大小,可知故6 ■ 2-6≤CD≤5.
二、关于综合题的教学思考
1.深刻理解综合题系列小问的关系,善于明辨“关联”.
综合题下设的系列小问通常都为并列式关系,但多数设计优秀的并列问题之间都存在着一定意义上的关联.教师备课时,不仅追求解题思路的贯通、答案的获取,还需要思考这些小问之间的关系有哪些,比如它们之间是否体现了从特殊到一般的成果扩大思想;是否属于一般中探究特例的由大到小的研究风格;上一问的解题策略是否对后一问获得思路具有启示、暗示作用;等等.教者想清辨明,则可以在后续备课时融入教学环节中.
2.解题教学时针对“上一问”互动讲评,即时链接“同类”.
综合题解题教学时,对上一问较为基础的习题有些初任教师常常“轻轻滑过”,缺少对这些基础问题的细致解读、对话追问,没有让学生在这样的教学对话过程中对这些基础问题背后的思想方法、设元意图、成果扩大提高认识、深刻理解,于是匆忙进入较难题的探究时,往往准备不足,解题思路或念头的出现较为奇巧、生硬,学生感觉思路“若从天上来”,不自然,对数学难题破解的策略感悟不深.我们认为,针对上一问的互动讲评要深入到命题者的意图探究,并适当成果扩大,让学生在这些追问对话中对前面的基础问题达到深刻理解的程度,为迎难而上、挑战难题作足准备、铺平垫稳.
3.解题教学之后加强反思与变式跟进,注重解后“回顾”.
近年来,《中学数学(下)》不少优秀解题教学课例都十分注意解后反思和变式跟进,这对我们的解题教学有很强的引领作用,笔者也深受教益,在日常教学中也注意变式跟进,有效反馈学生听课效果.作为本文的最后,我们也针对考题1,给出“变式再练”:
变式再练:如图1,已知抛物线C:y=(x+2)[t(x+1)-(x+3)],其中-7≤t≤-2,且无论t取任何符合条件的实数,点A、P都在抛物线C上.
(1)若点(1,a)在抛物线C上,求a的取值范围;
(2)点A在x轴上,过点A作线段AP的垂线交y轴于点B,交抛物线C于点D.
①求AP的长;
②求D点的坐标(用含t的式子表示);
③分析S△PAD的最值(包括最大值与最小值).
1.刘东升.并列式问题与递进式求解——由一则解题教学案例说起[J].中学数学教学参考(中),2012(8).
2.严君华.特例引路以退为进,逆向思考深化理解——以一道几何难题的思路突破为例[J].中学数学(下),2017(2).
3.季红妹.解题教学的追求:关联同类,感悟结构——从一道“网传错误解答”说起[J].中学数学(下),2017(2).
4.付小飞.明辨并列与递进,引导分离和聚焦——2016年江苏苏州中考第28题解析与教学思考[J].中学数学(下),2016(7).

