构建函数求解二元不等式问题的策略
湖南 石向阳 唐 亮
构建函数求解二元不等式问题的策略
湖南 石向阳 唐 亮
由于二元(或多元)不等式问题呈现形式复杂多样,解题思路灵活多变,具有结构独特、技巧性高、综合性强等特点,有时很难找到切入点.如果能灵活构建函数,并利用导数,往往能获得简捷解法.解决此类问题的关键就是怎样合理构建函数.从哪里入手,如何构建函数,构建什么样的函数?本文将就此问题做出探讨.
一、考虑导数运算法则构建函数
若题设中出现与导数有关的不等式,则往往是根据导数的运算法则计算后而设计的,所以我们应多从这个角度考虑如何构建函数.根据条件式特征,积极展开联想,借助求导法则,如和差求导、积商求导法则等,恰当构建函数,以便顺利解决目标问题.
【例1】已知f(x)是定义在(0,+∞)上的非负可导函数,且满足xf′(x)+f(x)≤0.对于任意正数a,b,若a<b,则必有 ( )
A.af(a)≤f(b) B.bf(b)≤f(a)
C.af(b)≤bf(a) D.bf(a)≤af(b)
【解析】方法1:设g(x)=xf(x),则g′(x)=xf′(x)+f(x)≤0(x>0),那么函数g(x)在(0,+∞)上是减函数(不一定是严格递减).因此,当b>a>0时,g(a)≥g(b),即af(a)≥bf(b).又bf(a)≥af(a),bf(b)≥af(b),所以bf(a)≥af(b),正确的选项为C.
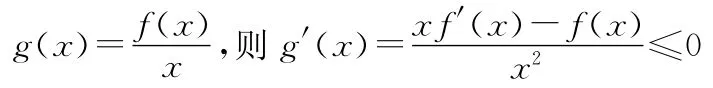
【评注】方法1利用积的求导法则构建函数,而方法2利用商的求导法则构建函数.在建构具体的函数时,需要对照题设中的条件,灵活应对.一般来说,有下面的规律:
1.含导数式f′(x)g(x)+f(x)g′(x)可构建函数:F(x)=f(x)g(x);
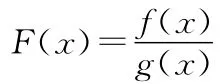
3.含导数式f′(x)+f(x)可构建函数:F(x)=f(x)ex;
5.含导数式f′(x)+af(x)可构建函数:F(x)=f(x)eax;
二、设定主元构建函数
在许多数学问题中,都含有常量、参量、变量等多个量.通常情况下,有一些元素处于突出和主导地位,可视之为主元;为了解决问题,也可人为突出某个量的地位作用,先将其当作主元;其他变元看作常数来构建函数,再用函数求导知识,结合函数单调性求解.

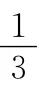
【变式1】设a≥b>0,求证:3a3+2b3≥3a2b+2ab2.
【证明】构建以a为主元的函数f(x)=3x3-3bx2-2b2x+2b3(x≥b),f′(x)=9x2-6bx-2b2=(3x-b)2-3b2≥b2≥0(x≥b),所以f(x)在x∈[b,+∞)上单调递增,得出f(a)≥f(b)=0.
【评注】视一个变量为主元,其他变量作常量来处理,这是多元不等式证明的一种重要思想.同时,主元策略还表现于主元选择的变通性,选择不同的主元,对于结构不对称的式子能形成不同的解题途径.
三、逆转主元构建函数
解决数学问题时,大多是从条件出发,借助于一些具体的模式和方法,进行正面的、顺向的思考.如果正向思维受阻,那么“顺难则逆、直难则曲、正难则反”.在多元不等式问题中,逆转主元思想常使思考产生新的源泉.
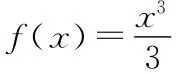
(1)当x>0时,f(x)≥gt(x)对任意正实数t成立;
(2)有且仅有一个正实数x0,使得g8(x0)≥gt(x0)对任意正实数t成立.
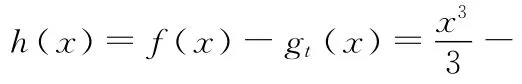
故当x>0时,f(x)≥gt(x)对任意正实数t成立.
因此当x>0时,f(x)≥gt(x)对任意正实数t成立.
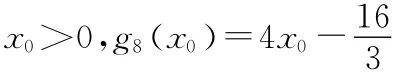
所以有且仅有一个正实数x0=2,使得g8(x0)≥gt(x0)对任意正实数t成立.
【评注】含参数问题通常含有两个或两个以上变元,习惯上我们把“x”当作自变量.第(1)问中的方法一就是以x为自变量构建函数求解,这是常规思路;方法二是视t为变量,x为常量,构建函数求解,这时就实现了自变量换位.这两种方法的可行性体现了变量的相对性.但对于第(2)问,如果仍把“x”当作自变量,这种思维定式就会把问题变得相当复杂,这时用逆转主元的思想将x与t角色换位,问题迎刃而解.一般地,可把已知范围的那个看作自变量,另一个看作常量.
四、巧妙消元构建函数
因为多元,所以通过消元来解决是很自然的想法.解题中,通过消元,消多为少、化繁为简、变难为易,常可降低思维难度.
【例4】设函数f(x)=2ax2+(a+4)x+lnx.
(1)讨论函数f(x)的单调区间;
(2)若函数y=f(x)的图象与x轴交于A,B两点,线段AB中点的横坐标为x0,证明f′(x0)<0.

①当a≥0时,对任意x>0,f′(x)>0,
∴此时函数f(x)的单调递增区间为(0,+∞).
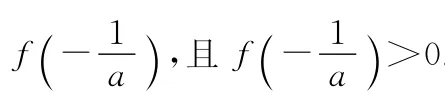
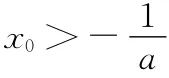


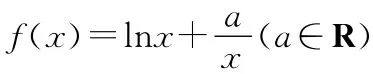
(1)讨论函数f(x)的单调区间及极值;
(2)若方程f(x)=2存在两个不同的实数解x1、x2,求证:x1+x2>2a.
【解析】(1)函数f(x)的定义域为(0,+∞),
①当a≤0时,f′(x)>0,f(x)的单调递增区间为(0,+∞),无极值.
②当a>0时,函数f(x)的单调递减区间为(0,a),单调递增区间为(a,+∞).f(a)为f(x)的极小值.
(2)因为方程f(x)=2存在两个不同的实数解x1、x2,不妨设x1<x2,所以f(x)必不能为单调函数,所以a>0.令F(x)=f(x)-2,则F(x)与f(x)的单调性相同,单调递减区间为(0,a),单调递增区间为(a,+∞).F(x)=f(x)-2=0存在两个不同的实数解x1、x2,所以最小值F(a)<0,且0<x1<a<x2.
要证x1+x2>2a成立,只需证x2>2a-x1.又因为0<x1<a2a-x1>a,所以x2、2a-x1∈(a,+∞),而当a>0时函数F(x)在区间(a,+∞)单调递增.所以等价于只要证明F(x2)>F(2a-x1),又F(x1)=F(x2)=0,即只需证明F(x1)>F(2a-x1).
下面证明:x∈(0,a],F(x)>F(2a-x).
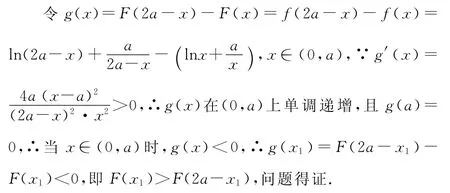
【评注】本题第(2)问,x1+x2>2ax2>2a-x1,利用函数的单调性转化为证明F(x2)>F(2a-x1),进一步转化为证明F(x1)>F(2a-x1),因而将两个变量的不等式问题,转化为一个变量的不等式问题.构建函数g(x)=F(2a-x)-F(x)<0=g(a),只需证明g(x)在x∈(0,a)上单调递增即可.
五、整体换元构建函数
在处理多变元函数问题中,用新元去代替该函数中的部分(或全部)变元.从而使变量化多元为少元,即达到减元的目的.问题中的参数减少了,复杂问题就简单化、明朗化了,这就是换元思想独到的作用.

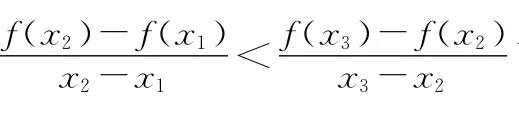
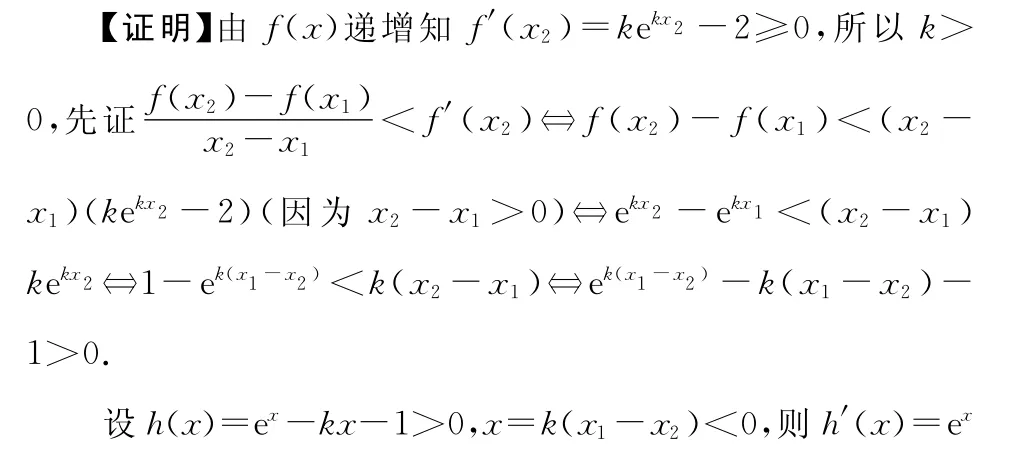

【评注】本题是多元不等式的证明,在变形过程中发现式子中出现一个整体k(x1-x2),此时巧妙地运用换元法化简式子,把二元问题化归为一元问题.构建函数使问题得以转化.一般地,变形过程中若出现指数形式ekx2-ekx1=ekx2[1-ek(x1-x2)],可考虑对k(x1-x2)作整体换元.
【变式2】同【例4】第(2)问.
【证明】不妨设A(x1,0),B(x2,0),且0<x1<x2.

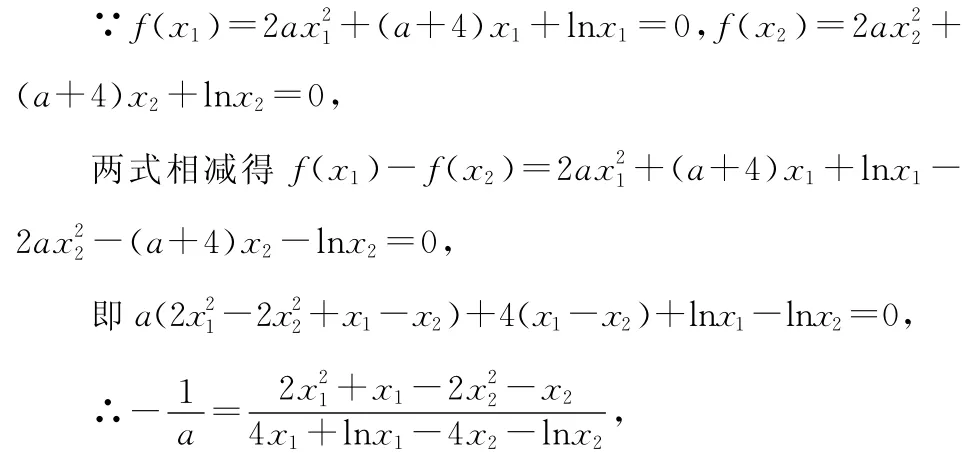


六、利用相似结构构建函数
有些多元不等式问题,可以通过分离变量,凸显出原不等式隐藏的规律,即左右两边式子的结构特征相似,这时可以构建函数,利用单调性解决.
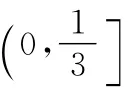
【分析】对原不等式进行变形,构建函数,利用函数的单调性,进行参变分离,求出a的取值范围.

【解】已知可转化为x1>x2>0时,mg(x1)-x1f(x1)>mg(x2)-x2f(x2)恒成立.
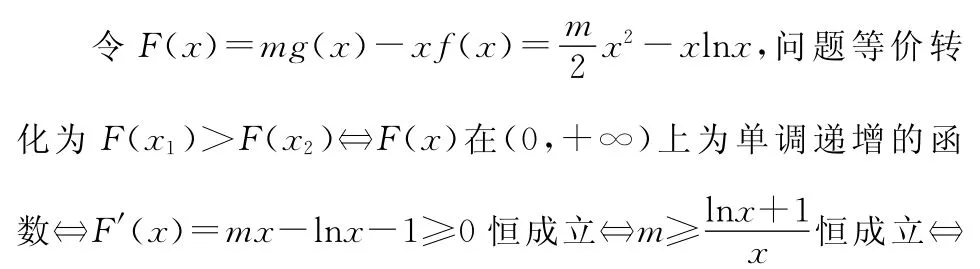

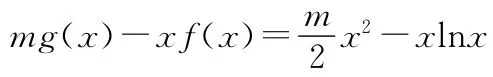
在根据特征构建函数时,需要有较强的观察和联想能力,灵活地针对不同的特征构建出相应的函数,这也需要我们平时注意积累,掌握一些常见解题模式.
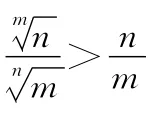
又如已知m,n是正整数,且2<m<n,求证:(1+m)n>(1+n)m.此问题求证的结论取对数后.构建函数f(x)=,只需证明f(x)在(2,+∞)上为减函数即可.
此两题不等式m,n位置交错,无法直接构建函数,考虑到是幂指数不等式,尝试两边取对数,发现原不等式变得非常“和谐”.再根据结构特征很容易构建出相应的函数.事实上,这种取对数使函数结构显露出来的方法是处理此类问题非常重要的手段.
通过上述几个例题可以看出,在求解多元不等式的问题中,我们可以通过类比、联想、抽象、概括等手段,构建出适当的函数,化多元问题为一元问题,并在此基础上利用函数的方法(如单调性)使原问题获解.它体现了数学中化归转化的思想,其中也渗透着猜想、探究等重要的数学思想.笔者认为这是函数思想解题的高层次体现.
(作者单位:湖南省长沙市雅礼教育集团南雅中学,湖南省长沙市教育科学研究院)

