二维Helmholtz方程的边界点解法

陈林冲

(重庆师范大学 数学科学学院， 重庆 401331)



二维Helmholtz方程的边界点解法

陈林冲

(重庆师范大学 数学科学学院， 重庆 401331)

针对二维Helmholtz方程的混合边值求解问题，采用边界点方法(boundary node method)，在直接边界积分方程的基础上，建立了求解Helmholtz方程边值问题的正则化形式，有效地避免了强奇异积分的计算，并且推导了弱奇异积分的计算公式。两个数值算例表明本方法可取得较高的可行性和有效性。

二维Helmholtz方程；混合边值问题；边界点法；强奇异积分；弱奇异积分

Helmholtz方程在工程技术、电磁场理论、散射理论、力学等较多领域有着广泛的应用，研究其数值解具有广泛的实际意义和重要的理论价值，尤其是对混合边值问题的处理[1]。传统的数值计算方法有有限差分法、有限元法、边界元法等。

有限差分法是将偏微分方程的定解问题按差分格式离散求解，但由于数值精度不稳定，很少用于物理工程问题的处理。有限元法将问题所在的区域离散为有限单元，在单元上对求解变量建立基于节点的插值函数近似，以变分原理或加权残数法建立控制方程，联立数值积分建立相关的代数方程组，但是它需要在整个区域上进行离散，在处理大变形以及动态裂纹扩展等问题时，网格可能会发生畸变，此时必须进行网格重构，从而损失了精度。边界元法[2]是继有限元法之后的一种基于边界单元和节点的数值方法，是将偏微分方程的定解问题转化为边界积分方程，并对求解区域的边界进行单元离散而形成的数值方法，必须要建立与插值节点拓扑相关的网格。对于复杂方程，不仅需要克服基本解的奇异性，还要进行必要的网格重构，增加计算时间，降低精度。因此，为了克服基于网格(单元和节点)的数值方法对于单元或网格的依赖，保证计算精度,节约计算时间，产生了一种不需要与节点相关联网格的新型数值计算方法——无网格方法，并且近年来得到了较大的发展[3-4]。

最早的无网格方法是1977年Lucy提出的光滑粒子法[5]，主要用于研究无边界的天体问题和流体问题，但稳定性不是很好。1981年，Lancaster等建立了移动最小二乘法[6]，采用完备多项式作为基函数，利用误差的加权平方和构造泛函，得到的逼近函数精度高、光滑性好，函数本身和其导函数都连续。20世纪90年代，Nayroles和Belytschko等将移动最小二乘法引入微分方程的边值问题中[7]，后来Mukherjee等对移动最小二乘法进行了改进，提出了求解势问题和弹性力学问题的边界点法(Boundary Node Method)[8-11]。边界点法是将移动最小二乘法导出的插值公式与边界积分方程结合起来，通过边界积分方程的边值条件，建立边界上的线性方程组,计算时间快，效率高。

本文致力于用边界点方法数值求解二维Helmholtz方程。利用格林公式(Green)得到Helmholtz方程的直接边界积分方程，相比间接的层位势理论建立的间接边界积分方程更适用于混合问题。由于二维Helmholtz方程基本解为特殊函数，将其展开成了一种级数形式，巧妙地利用二维Laplace方程的基本解的特性，建立了二维Helmholtz方程的正则化的边界积分方程，有效地避免了强奇异积分的计算。针对其中含基本解的弱奇异积分项，详细地推导了其数值计算公式[12]。最后给出了数值算例,验证了该方法的可行性和有效性。

1 Helmholtz方程混合边值问题

1.1 直接边界积分方程及其正则化形式

考虑如下二维Helmholtz方程混合边值问题：

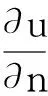
利用格林公式得到Helmholtz方程的解的表达式和边界积分方程[13]：

(1)

(2)

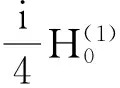
其中c≈0.577 215 664 9，为欧拉常数，则有

定理1 当kr很小时,二维Helmholtz方程的正则化形式为

(3)

证明 在式(2)中代入其展开级数得

所以有

因此

定理得证。

1.2 边界点方法求解二维Helmholtz方程

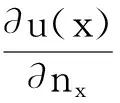
其中，φl(x)为移动最小二乘法(MLS)的形函数[15-17]。

设在边界Γu上N1有个边界节点，则Γq上有N-N1个边界节点，代入直接边界条件形成线性方程组

在式(1)中，∀y∈Ω有

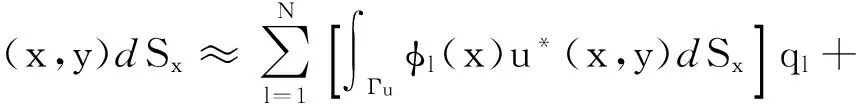
(4)

1.3 积分的计算

将边界Γ划分成N个积分背景网格Γn，n=1,…,N。Γn选为直线段，可表示为

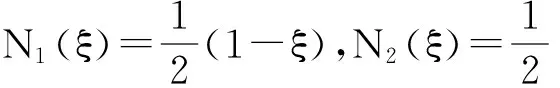
其中，

(xp,yp)∈Γn，所以有

则有

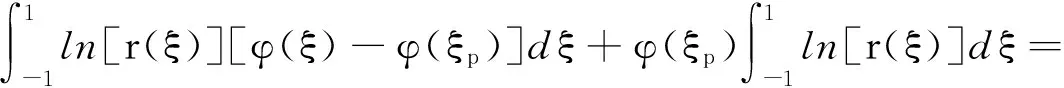
对于后一个积分I2，采用分部积分公式得

所以

2 数值算例

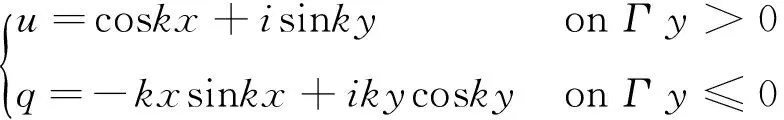
为了误差估计和收敛阶的研究，定义下面的评估方式[18]：

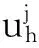
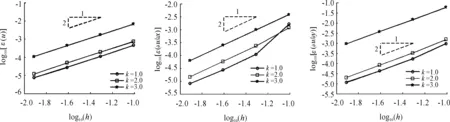
图的误差

从图1中可以看出：当k取不同值时，函数本身和它的一阶导函数的收敛阶都在2左右；从图2中可以看出：当k取不同值时，函数本身和它的一阶导函数的收敛阶都在3左右，都取得了较好的数值效果。

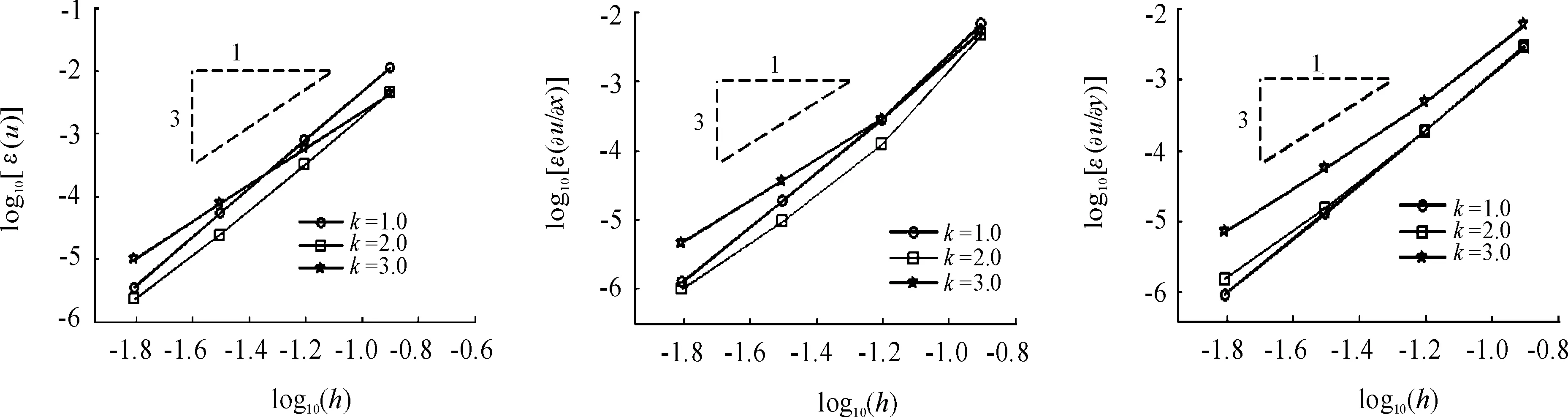
图的误差

3 结束语

在已有的直接边界积分方程理论的基础上，本文建立了二维Helmholtz方程混合边值问题的正则化边界积分方程，有效地避免了强奇异积分的计算，引入了弱奇异积分的处理方法。采用边界点方法(Boundary Node Method)得到了较高的精度和收敛阶，2个数值算例验证了该方法的可行性和有效性。进一步地，可以发现由于正方形区域的特殊性，它所布置的节点刚好落在正方形区域的边界上，没有产生几何误差，因此其得到的收敛阶要比圆域得到的收敛阶更高一些。

[1] ERLANGGA Y A.A Robust and Efficient Iterative Method for the Numerical Solution of the Helmholtz Equation[D].Delft:Technische Universit Delft,2005.

[2] 嵇醒，臧跃龙，程玉民.边界元进展及通用程序[M].上海：同济大学出版社，1997.

[3] BELYTSCHKO T,KRONGAUZ Y,ORGAN D.Meshless methods:An overview and recent developments[J].Computer Methods in Applied Mechanics and Engineering,1996,139(1/4):3-47.

[4] YAGAWA G,FURUKAWA T.Recent developments of free mesh method[J].International Journal for Numerical Methods in Engineering,2000,47(8):1419-1443.

[5] LUCY L B.A numerical approach to the testing of the fission hypothesis[J].The Astron J,1977,8(2):1013-1024.

[6] LANCASTER P,SALKAUSKAS K.Surfaces generated by moving least square methods[J].Mathematics of Computation,1981,37:141-158.

[7] NAYROLES B.Generalizing the finite element method:Diffuse approximation and diffuse elements[J].Computational Mechanics,1992,10:307-318.

[8] MUKHERJEE Y X,MUKHERJEE S.The boundary node method for potential problems[J].International Journal for Numerical Methods in Engineering,1997,40(5):797-815.

[9] KOTHNOR VS,MUKHERJEE S,MUKHERJEE Y X.Two dimensional linear elasticity by the boundary node method[J].International Journal of Solids and Structures,1999,36(8):1129-1147.

[10]CHATI M K,MUKHERJEE S,MUKHERJEE Y X.The boundary node method for three-dimensional linear elasticity[J].International Journal for Numerical Methods in Engineering,1999,46(8):1163-1184.

[11]CHATI M K,MUKHERJEE S.The boundary node method for three-dimensional problems in potential theory[J].International Journal for Numerical Methods in Engineering,2000,47(9):1523-1547.

[12]SRINIVAS T,SUBRATA M.An extended boundary node method for modeling normal derivative discontinuities in potential theory across edges and corners[J].Engineering Analysis with Boundary Elements,2004,28:1099-1110.

[13]祝家麟，袁政强.边界元分析[M].北京：科学出版社，2009.

[14]王竹溪，郭敦仁.函数论-特殊函数概论[M].北京：国防工业出版社，1983.

[15]张雄，刘岩.无网格法[M].北京：清华大学出版社，2004.

[16]孙新志，李小林.复变量移动最小二乘近似在Sobolev空间中的误差估计[J].应用数学和力学,2016,37(4):416-425.

[17]程玉民.无网格方法[M].北京：科学出版社，2015.

[18]LI X L,ZHANG S G.Meshless analysis and applications of a symmetric improved Galerkin boundary node method using the improved moving least-square approximation [J].ELSEVIER.Applied Mathematical Modelling,2016(40):2875-2896.

(责任编辑 陈 艳)

Boundary Node Method for the 2-D Helmholtz Equation

CHEN Lin-chong

(School of Mathematical Science, Chongqing Normal University, Chongqing 401331, China)

Aiming at 2D Helmholtz equation mixed boundary problem, based on the boundary node method, the regularized form to 2D Helmholtz equation boundary value problem is given on the foundation of direct boundary integral equation. The method can effectively avoid strongly singular integral, and it also deduces a calculating formula to weakly singular integral in detail. Two numerical examples demonstrate that this method has the high feasibility and efficiency.

2D Helmholtz equation; mixed boundary problem; boundary node method; strongly singular integral; weakly singular integral

2017-04-18

国家自然科学基金资助项目(11471063)；重庆市基础科学与前沿技术研究重点项目(cstc2015jcyjBX0083)

陈林冲(1988—)，男，硕士，主要从事计算数学研究，E-mail:794530653@qq.com。

陈林冲.二维Helmholtz方程的边界点解法[J].重庆理工大学学报(自然科学)，2017(7):188-194.

format：CHEN Lin-chong.Boundary Node Method for the 2-D Helmholtz Equation[J].Journal of Chongqing University of Technology(Natural Science)，2017(7):188-194.

10.3969/j.issn.1674-8425(z).2017.07.030

O242.2

A

1674-8425(2017)07-0188-07