基于ADMM算法正则化最优步长的研究

陈庆国,赵建伟,曹飞龙

(中国计量大学 理学院,浙江 杭州 310018)

基于ADMM算法正则化最优步长的研究

陈庆国,赵建伟,曹飞龙*

(中国计量大学 理学院,浙江 杭州 310018)

交替方向乘子法(Alternating Direction Method of Multipliers,简称ADMM)已经成为求解大规模结构性优化问题的有效方法。尽管已经有较多关于ADMM算法收敛性的研究,但关于该算法参数对收敛性影响的定量表示仍须进一步研究,已有的结果中仅是在实验中凭经验对步长进行选取。文章研究ADMM算法l1正则化最小的一个重要问题Lasso的收敛因子。研究发现解的形式可用软阈值算子表示,分析发现软阈值的三种情况可以等价转化成算法收敛因子的两种情况,然后通过最小化收敛因子解出最优的步长。实验表明,应用该方法选出的步长,其相应算法的收敛速度明显快于其他选取步长的情况。此外,将该方法应用到压缩感知问题,给出了一个计算最优步长的近似值策略,获得了较好的实验效果。

交替方向乘子法;收敛速率;最优步长;最优算法;压缩感知

0 引言

利用交替方向乘子法(Alternating Direction Method of Multipliers,简称 ADMM)求解结构化的凸优化问题是十分有效的。该方法早在20世纪70年代就已经被提出,类似的思想可追溯到五十年代中期[1]。从数学上讲,ADMM既有乘子法的强收敛性质又有对偶上升法的分解性。因此,该方法比较适合求解大规模的优化问题。至今,该方法已经在诸多领域得到广泛应用,如压缩感知[2]、正则化估计[3]、图像处理[4]、机器学习[5]和无线传感网络资源分配[6]等。对偶分解是一个经典的数学思想,可以追溯到20世纪60年代早期[1]。因其在求解大规模的线性问题上十分有效而被人们熟知[7-8],主要用来产生并行化的算法。如果优化问题结构合理,应用对偶分解技术,原问题则可以在多个处理器上应用梯度下降法或次梯度法进行分布式计算,从而得到一个全局最优解。如果问题的参数如损失函数的利普希兹(Lipschitz)常数可知,则最优步长和相关的收敛性是可知的[9]。然而,梯度法存在缺点,即它对步长的选择非常敏感,选择不合适的步长甚至会导致算法不收敛。

然而,ADMM对步长具有较强的鲁棒性。在一定的条件下,该方法能保证对所有的步长都收敛。近来,为了研究ADMM算法的收敛速率,人们做了很多工作。文献[10]指出,如果目标函数是强凸的并且具有利普希兹连续梯度,那么由ADMM算法产生的迭代在一定距离度量内可以线性收敛到最优解。需要强调的是,虽然ADMM算法具有线性收敛速率,但是收敛所需迭代次数或者收敛时间仍然严重依赖于算法的步长。本文将展示选择一个较差的步长将会导致ADMM算法收敛需要较长的时间。一些最近的论文研究了关于分布式凸优化问题ADMM算法的最优步长选择问题,如文献[11-12]。文献[10]给出了当目标函数是强凸且具有利普希兹连续梯度时的推荐步长,文献[13]首次给出了ADMM求解二次规划问题最优步长的选择方法,结果更加精确,但该方法要求约束矩阵行满秩,这给实际应用带来了一定的限制。文献[14]对文献[13]的方法做了改进,不再需要约束矩阵满足行满秩这一条件,并给出了最优步长并证明了算法的收敛性。

就我们所知,至今尚无关于l1正则化ADMM算法的最优步长的研究,受文献[13]的启发,对于Lasso问题,在一定的条件下,对软阈值的分段分析发现,对应的收敛因子只有两种情况。通过最小化ADMM迭代算法的收敛因子,计算出使收敛因子最小的步长,此时算法收敛速度最快。实验结果表明,相对于经验性选择的步长,我们的方法所给出的最优步长大大加快了ADMM算法的收敛速度,这对类似的实验步长的选择都具有指导意义。

文中符号说明:我们定义R为实数集,I是单位矩阵,所有的向量都是列向量,给定一个矩阵A∈Rm×n,AT表示矩阵A的转置矩阵,对于一个方阵B∈Rn×n,λi(B)表示矩阵B的第i个特征值,λmax(B)和λmin(B)分别表示矩阵B的最大特征值和最小特征值。

1 压缩感知背景和ADMM算法

1.1 压缩感知

利用压缩感知成功重构稀疏信号有两个关键要素,一个是传感矩阵;另一个是信号重构算法[15]。传感矩阵A须包含足够的原始稀疏信号的信息,Candès和Tao证明了传感矩阵必须满足约束等距性条件[16],Baraniuk在文献[17]中给出约束等距性的等价条件是测量矩阵和稀疏表示的基不相关,文献[16]、[18]证明了当测量矩阵是高斯随机矩阵时,传感矩阵能以较大概率满足约束等距性条件。压缩感知的核心是信号重建算法,Candès等人证明信号重建问题可以通过求解如下l0范数问题解决[16],

min ‖x‖0

s.t.Ax=b.

但最小l0范数问题是一个NP-hard问题[19]。研究人员提出了一系列求得次优解的算法,其中一个方法是把l0范数替换为l1范数[20]:

min ‖x‖1

s.t.Ax=b.

文献[21-22]证明了在一定条件下,二者是等价的,其中A∈Rm×n(m≪n)是观测矩阵,要求满足约束等距性条件,一般为高斯矩阵,本文的实验也是选择高斯矩阵作为观测矩阵,y∈Rm是观测向量,x∈Rn是待重构的信号。引入重构误差,上述问题转化为

min ‖x‖1

s.t. ‖Ax-b‖2≤ε.

1.2 ADMM算法

ADMM算法主要用于解决如下形式的优化问题:

minf(x)+g(z)

s.t.Ax+Bz=c,

(1)

其中f和g都是凸函数,x∈Rn,z∈Rm,A∈Rp×n,B∈Rp×m,c∈Rp,一般地,f是损失函数,g是正则项,更详细的说明可见文献[1]。求解该优化问题主要依靠其增广拉格朗日函数:

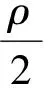
由此,按顺序更新变量x和变量z,然后再更新对偶变量:

μk+1=μk+ρ(Axk+1+Bzk+1-c).

(2)

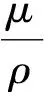
uk+1=uk+Axk+1+Bzk+1-c.

(3)

当变量x和z的更新能很有效地计算时,例如它们具有封闭形式的解,那么整个ADMM算法是非常有用的。具有封闭形式的解的情形有线性和二次规划、基追踪、l1正则化最小问题、模型拟合等,完整的讨论见文献[1]。ADMM算法的优点是仅有一个参数ρ,并且在一定的条件下,该方法对任意参数均收敛[23]。正如我们在第一节中所说,ADMM算法与梯度法形成对比,如果步长参数选择得太大,则梯度法会发散。尽管如此,步长依然对ADMM算法的收敛因子有直接影响。ADMM的收敛性用残差来刻画,原始残差和对偶残差分别是

rk+1=Axk+1+Bzk+1-c

sk+1=ρATB(zk+1-zk).

下面我们讨论某些情况下ADMM算法的收敛性并推导出使收敛因子最小的步长的显式表达式。

2 l1正则化最小问题的最优收敛因子

在统计学、机器学习和控制论中,正则化估计问题是极其常见的,一般

minf(x)+λg(x),

(4)

其中损失函数f(x)可以是任意的凸函数,后一项g(x)是正则项,λ是正则化参数且大于0,加入正则项的目的一般是为了防止过拟合,常见的有l1正则项和l2正则项,l1正则项使解具有稀疏性,这种稀疏性十分重要。在机器学习等领域中,稀疏性问题随处可见,当(4)式的正则项是l1正则项时,它的一个重要特例是l1正则线性回归,也叫Lasso问题,关于Lasso问题更详细的背景可以查看文献[24-25],具体如下:

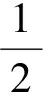
(5)

其中A∈Rm×n,b∈Rm,把上面的Lasso问题写成ADMM形式:

minf(x)+g(z)

s.t.x-z=0,

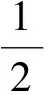
xk+1=(ATA+ρI)-1(ATb+ρ(zk-uk))

uk+1=uk+xk+1-zk+1,

(6)

其中zk+1是软阈值形式的解,软阈值算子S的定义为

这说明软阈值算子是一个收缩算子。为方便后面的计算,根据上面软阈值算子的定义,把zk+1的解写成如下分段形式:

(7)

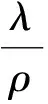
(8)

令z*是该问题的不动点,即z*=Ez*+C,那么对偶误差ek+1=zk+1-z*,即

ek+1=Eek.

(9)

对偶误差收敛当且仅当矩阵E的谱半径小于1,为了表示E的特征值,令λi(ATA)为ATA的特征值,则E的特征值为:

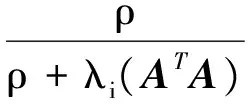
(10)

很明显,当ATA的特征值大于零时,此时(10)式是小于1的,算法是收敛的。因此,求解最优的步长等价于求解如下的优化问题:

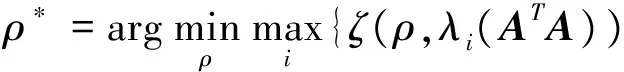
(11)

从(10)式可知,ζ(ρ,λi(ATA))关于λi(ATA)是单调递减的,所以有

(12)

我们暂不做进一步处理,先考虑第二种和第三种情况下最优步长的结果。

当zk+1的迭代从开始到收敛都是(7)式中的第二种情况时,把zk+1=0代入到(6)式中,

(13)

类似于上面的做法,此时算法收敛当且仅当矩阵E的谱半径小于1,令λi(ATA)为ATA的特征值,此时E的特征值为:

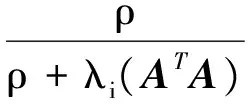
(14)

同样地,当ATA的特征值都大于零时,(14)式是恒小于1的,求解最优的步长等价于求解如下的优化问题:

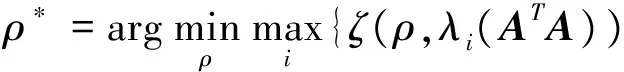
(15)

由(14)式可知,此时ζ(ρ,λi(ATA))关于λi(ATA)是单调递增的,所以(15)式可以写成

(16)

该结果类似于第一种情况的(12)式。

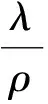
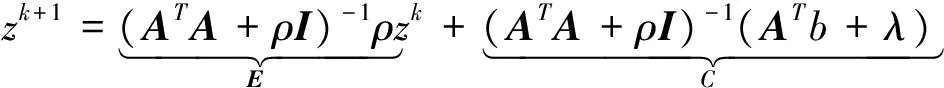
(17)

最终的求解最优步长的优化问题:

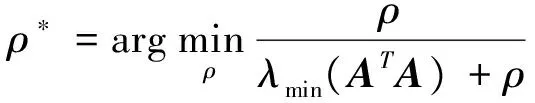
(18)

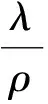
(19)

即z等于零和不等于零的情况,对应的矩阵E的谱半径为

(20)

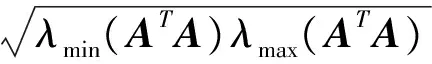
(21)

对应的收敛因子:

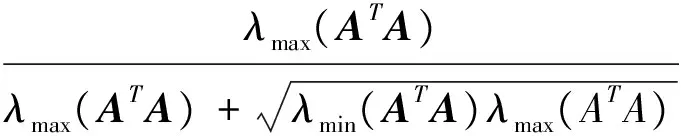
(22)

3 实验

3.1 Lasso问题

为验证本文结论的正确性,我们先考虑一个l1正则最小问题,给出最优步长和收敛性情况。模型为(5)式,其中

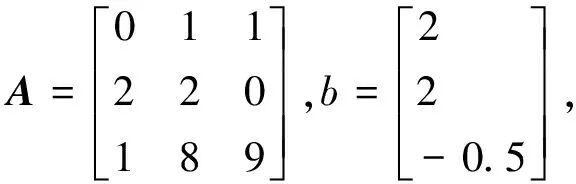
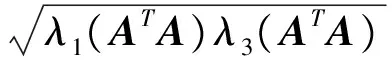
当选取最优的步长时,ADMM算法迭代13次达到收敛,表1给出了迭代过程中z的值,此时向量z是三维的,迭代次数为1时z=0表示初始值选取零向量。在后续整个迭代中,z1和z3都不等于零,说明它们是按照(16)式的第一种情况更新的,z2在整个迭代中几乎都等于零,有一步迭代不等于零,整个算法的迭代方式与我们之前的假设相符,图1中的理论最优步长和实际结果也相符,这也验证了第三节方法的正确性。

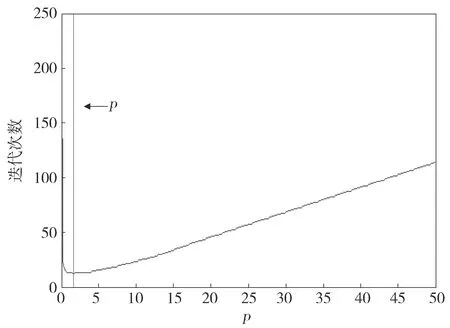
Fig.1 Iterative results图1 迭代结果

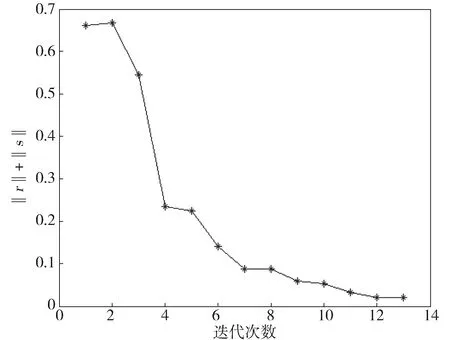
Fig.2 Convergence of the optimal step size图2 最优步长时算法的收敛情况

表1 步长最优时,迭代到收敛的z的值Table 1 Iteration value of z when the step size is optimal

3.2 压缩感知应用

下面在压缩感知背景下测试本文所提出的方法,A∈Rm×n,m=1 500,n=5 000,观测矩阵A服从均值为0、方差为1的高斯分布。选择观测矩阵为高斯矩阵,待恢复信号的稀疏度比p=0.02。此时,矩阵A不再是列满秩矩阵,ATA的特征值中前(n-m)个元素都为0。为了保证算法收敛,λmin(ATA)用ATA的特征值的最小非零元来代替,得到一个理论最优值的近似,图3横坐标是步长,纵坐标是算法收敛时的迭代次数,红线所示ρ*=2.34是理论值,观察可以看到在此位置蓝色曲线也是最低点,也正是收敛所需的实际最少迭代次数的步长。此时信号长度为5 000,稀疏度为100,这说明4 900个元素最后都为0,也就是说它们在收敛时的迭代公式都是(19)式zk+1=0,在迭代过程中总是会出现不等于零的情况。同样地,100个非零元素在收敛时等于零,但在迭代过程中,会出现等于零的情况。总的来说,这符合上面的假设条件,所以理论最优步长的近似和实际最优值相吻合。

本文算法对应的收敛条件是对偶误差与原始误差的和不超过10-5,图4展示了最优步长和其他步长时的收敛情况,最优步长只需要30次迭代达到收敛,收敛速度明显快于其他步长。从图上来看,当步长选择过小时,算法收敛需要更多的迭代次数,这是因为过小的步长需要更多的迭代次数才能到达最优解。当步长选择过大时,同样会需要较多的迭代次数,因为有可能会走过最优解,从而“回头”继续寻找,可能需要反复多次寻找才能找到最优解。特别注意的是当步长为1时,这也是很多实验的经验选择,而本实验结果表明它并不是最好的。在图4中,尽管在前10次迭代中,步长为1时的收敛速度要快于最优步长的情形,但从后续的迭代直到收敛这一过程,最优步长的收敛速度远快于步长为1的情况,也远快于其他步长的情况,且最先达到收敛,说明最优步长的收敛速度快于一般的默认步长。图5则是局部细节图,更加直观。

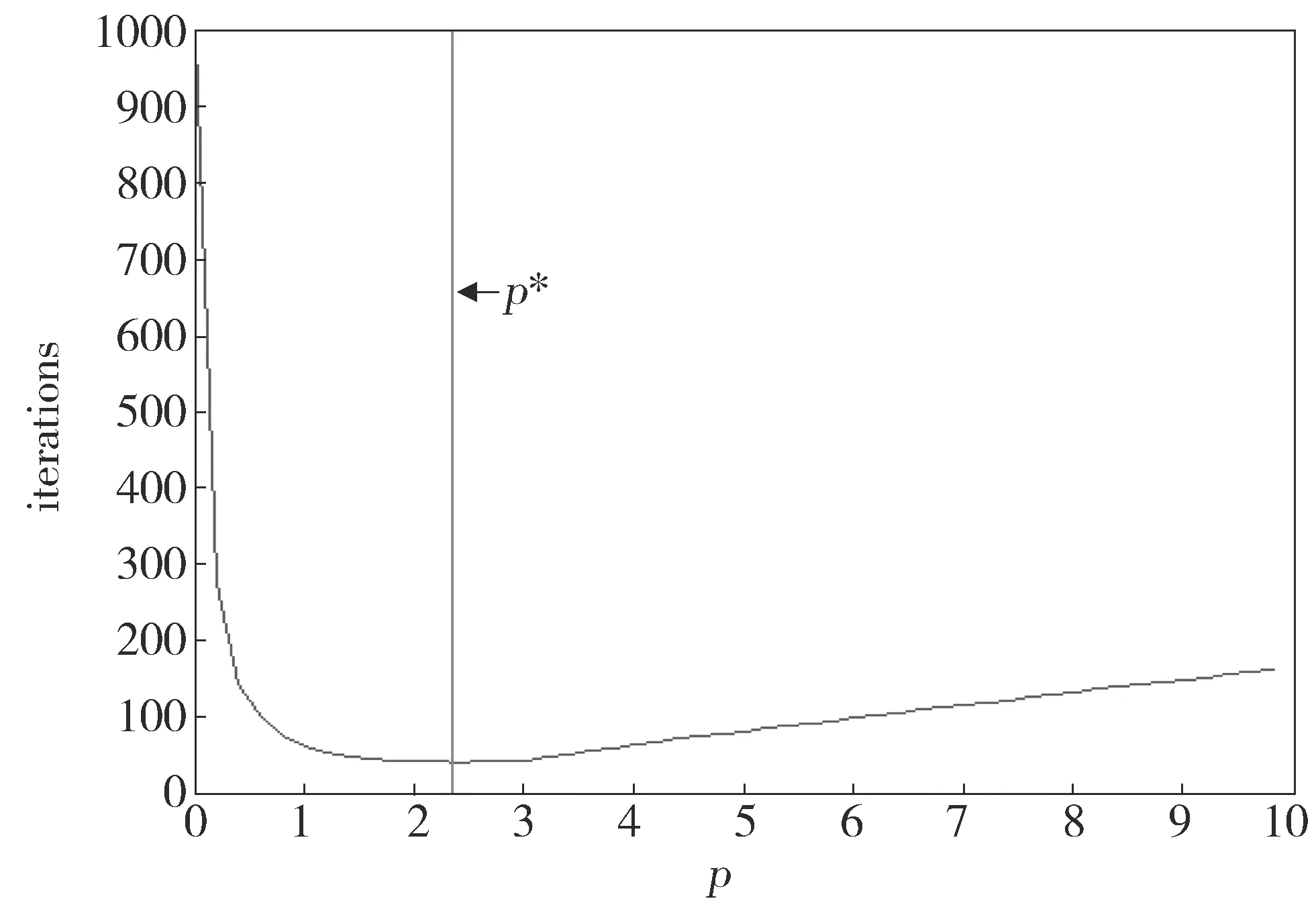
Fig.3 Optimal step size in the compression sensor图3 压缩感知背景下的最优步长

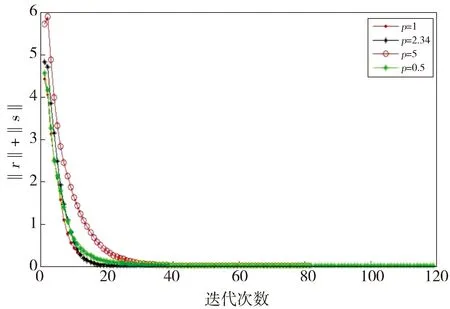
Fig.4 Number of convergence iterations under different steps图4 不同步长下的ADMM算法的收敛速度

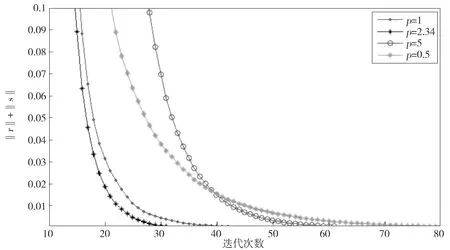
Fig.5 Local details of figure 4图5 图4局部细节

3.3 考虑稀疏度比的变化

鉴于压缩感知针对稀疏信号重构问题。信号的稀疏性变化,对应的迭代步长如何变化,是一个值得研究的问题。根据第三节的推导,信号稀疏度越大,则说明向量z更新的情况更多的是(19)式第二种情况。取观测矩阵为A∈R550×1 000且是高斯矩阵,在其它条件不变,不同稀疏度比例的情况下,图6展示了最优步长和迭代次数的关系。横坐标是步长,纵坐标是迭代次数,其中任意一条曲线表示选择对应稀疏度比时,不同步长下算法达到收敛时所需迭代次数。通过分析图6,我们发现在8种不同稀疏度比中,它们的最优步长没有变化,即这些曲线的最低点相同,并且是8条曲线的最低点,对应的理论最优值也重叠在了一起,如图6中所指竖线,它们的不同体现在当步长选择偏大时,对应的迭代次数不同。这也可以解释,根据上一节提出的最优步长的理论,最优步长只跟观测矩阵有关,信号的稀疏度并不影响结果,图6的结果证明了这一点。

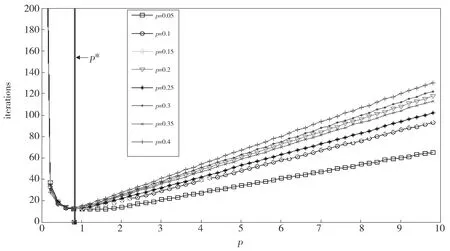
Fig.6 Optimal step size of ADMM under different sparse degree ratio图6 不同稀疏度比下ADMM算法的最优步长

4 结论

本文研究了ADMM算法关于Lasso问题的最优步长问题。对软阈值算子进行分析,发现对应的收敛因子可以简化成两种情况,推导出算法的收敛因子,通过最小化收敛因子给出使算法收敛速度最快的参数的显示表达式,我们用数值仿真实验验证了分析结果。当本文方法应用到压缩感知问题时,由于观测矩阵A不是列满秩的,λmin(ATA)等于零,这会导致算法不收敛。为了解决这个问题,我们用ATA的特征值的最小非零元来代替λmin(ATA),这样保证了算法的收敛性,虽然得到的步长只是最优值的近似,但实验表明此时算法收敛的速度仍然明显快于其他步长的情形。最后做了改变信号稀疏度的实验,最优步长的选择并没有改变,与上述结果相符。本文提出的针对l1正则最小问题的ADMM算法的步长选择方法简单且有效,因为经验性的选取步长往往不是最优的,本文的方法能准确找到最优步长,对类似的实验都具有一定的指导意义。

本文一个可以改进的地方是,在压缩感知的背景下,观测矩阵A∈Rm×n的行数远小于列数,即观测次数远小于稀疏信号长度,此时ATA的前(n-m)个特征值都是0,而λmin(ATA)不能等于零,我们用最小非零元来替代,得到一个最优解的近似,尽管这个近似解效果也较好,但我们认为是可以得到准确的最优步长的,如何解决这个问题是需要进一步研究的。

[1] Boyd S,Parikh N,Chu E,etal.Distributed Optimization and Statistical Learning Via the Alternating Direction Method of Multipliers[J].FoundationsandTrendsinMachineLearning,2011,3(1):1-122.DOI:10.1561/2200000016.

[2] Yang J,Zhang Y.Alternating Direction Algorithms forl1-problems Incompressive Sensing[J].SIAMJournalonScientificComputing,2011,33(1):250-278.DOI:10.1137/090777761.

[3] Wahlberg B,Boyd S,Annergren M,etal.An ADMM Algorithm for a Class of Total Variation Regularized Estimation Problems[C]∥Proc. 16th IFAC Symposium on System identification,Brussels,Belgium,IFAC Proceedings Volumes:2012,45(16):83-88.DOI:10.3182/20120711-3-BE-2027.00310.

[4] Figueiredo M,Bioucas-Dias J.Restoration of Poissonian Imagesusing Alternating Direction Optimization[J].IEEETransImageProcessing,2010,19(12):3133-3145.DOI:10.3182/20120711-3-BE-2027.00310.

[5] Forero P A,Cano A,Giannakis G B.Consensus-based Distributed Linear Support Vector Machines[C]∥Proceeding IPSN’10 proceeding of the 9th ACM/IEEE International Conference on Information Processing in Sensor Networks,2010:35-46.DOI:10.1145/1791212.1791218.

[6] Joshi S,Codreanu M,Latva-aho M.Distributed Resource Allocation for MISO Downlink Systems Via the Alternating Direction Method of Multipliers[J].EURASIPJournalonWirelessCommunicationsandNetworking,2014,2014(1).DOI:10.1186/1687-1499-2014-1.

[7] Benders J F.Partitioning Procedures for Solving Mixed-variables Programming Problems[J].NumerischeMathematik,1962,4(1):238-252.DOI:10.1007/bf01386316.

[8] Dantzig G B,Wolfe P.Decomposition Principle for Linear Programs[J].OperationsResearch,1960,8(1):101-111.DOI:10.1287/opre.8.1.101.

[9] Nesterov Y.Introductory Lectures on Convex Optimization:A Basic Course[J].AppliedOptimization,2004，85(5)：ⅹⅷ，236.DOI:10.1007/978-1-4419-8853-9.

[10] Deng W，Yin W.On the Global and Linear Convergence of the Generalized Alternating Direction Method of Multipliers[J].JournalofScientificComputing,2015,66(3):889-916.DOI:10.1007/s10915-015-0048-x.

[11] Teixeira A,Ghadimi E,Shames I,etal.Optimal Scaling of the ADMM Algorithm for Distributed Quadratic Programming[C]∥Proc.52nd IEEE Conference on Decision Control (CDC).Florence,Italy:IEEE,2013.DOI:10.1109/CDC.2013.6760977.

[12] Shi W,Ling Q,Yuan K,etal.On the Linear Convergence of the ADMM in Decentralized Consensus Optimization[J].IEEETransactionsonSignalProcessing,2014,62(7):1750-1761.DOI:10.1109/tsp.2014.2304432.

[13] Ghadimi E,Teixeira A,Shames I,etal.Optimal Parameter Selection for the Alternating Direction Method of Multipliers(ADMM):Quadratic Problems[J].IEEETransactiononAutomaticControl,2015,60(3):644-658.DOI:10.1109/tac.2014.2354892.

[14] Raghunathan A U，Cairano S D.Alternating Direction Method of Multipliers for Strictly Convex Quadratic Problems:Optimal Parameter Selection[C]∥American Control Conference(ACC).2014:4324-4329.DOI:10.1109/acc.2014.6859-093.

[15] 李树涛,魏丹.压缩传感综述[J].自动化学报,2009,35(11):1369-1377.

[16] Candès E J,Tao T.Decoding by Linear Programming[J].IEEETransactionsonInformationTheory,2005,51(12):4203-4215.DOI:10.1109/tit.2005.858979.

[17] Baraniuk R G.Compressive Sensing[J].IEEESignalProcessingMagazine,2007,24(4):118-121.DOI:10.1109/MSP.2007.4286571.

[18] Candès E J,Romberg J,Tao T.Stable Signal Recovery From in Complete and Inaccurate Measurements[J].CommunicationsononPureandAppliedMathematics,2006,59(8):1207-1223.DOI:10.1002/cpa.20124.

[19] Donoho D L.For Most Large Underdetermined Systems of Linear Equations,the Minimall1Norm Solution is Also the Sparsest Solution[J].CommunicationsonPureandAppliedMathematics,2006,59(6):797-829.DOI:10.1002/cpa.20132.

[20] Candès E J,Romberg J,Tao T.Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Information[J].IEEETransactionsonInformationTheory,2006,52(2):489-509.DOI:10.1109/tit.2005.862083.

[21] Chen S B,Donoho D L,Saunders M A.Atomic Decomposition by Basis Pursuit[J].SIAMJournalonScientificComputing,1998,20(1):33-61.DOI:10.1137/s1064827596304010.

[22] Donoho D L,Elad M,Temlyakov V N.Stable Recovery of Sparse Over Complete Representations in the Presence of Noise[J].IEEETransactionsonInformationTheory,2006,52(1):6-18.DOI:10.1109/tit.2005.860430.

[23] Eckstein J,Yao W.Augmented Lagrangian and Alternating Direction Methods for Convex Optimization:A Tutorial and Some Illustrative Computational Results[R].RUTCOR Research Reports 32:2012.

[24] Hastie T,Tibshirani R,Friedman J.The Elements of Statistical Learning:Data Mining,Inference and Prediction.Springer,second ed,2009.

[25] Tibshirani R.Regression Shrinkage and Selection Via the Lasso:a Retrospective[J].JournaloftheRoyalStatisticalSociety:SeriesB(StatisticalMethodology)，2011,73(2):273-282.DOI:10.1111/j.1467-9868.2011.00771.x.

ResearchOnRegularizationOptimalStepSizeofADMMAlgorithm

CHEN Qingguo,ZHAO Jianwei,CAO Feilong*

(CollegeofScience,ChinaJiliangUniversity,Hangzhou310018,China)

The alternative direction method of multipliers (ADMM) has become an effective method to solve large-scale structural optimization problems.Although there are many studies on the convergence of the ADMM algorithm, the quantitative expression of the impact of the algorithm parameters on the convergence still needs to be further studied. It is only in the experiment that the step size is selected empirically.We study the convergence of Lasso which is an important problem ofl1regularized minimization.The results indicated that the form of the solution can be expressed by soft thresholding operator, and the three cases of soft thresholds can be equivalently transformed into two cases of algorithm convergence factor. The optimal step size is then solved by minimizing the convergence factor.The experimental results show that the convergence rate of the proposed algorithm is faster than that of other steps.In addition, when the method is applied to the problem of compressive sensing, an approximate strategy for calculating the optimal step size is given, and a better experimental result is obtained.

ADMM;convergence rate;optimal step-size;optimal algorithm; compressive sensing

10.13451/j.cnki.shanxi.univ(nat.sci.).2017.04.001

2017-04-12；

2017-05-26

国家自然科学基金(61672477；61571510)

陈庆国(1992-)，男，硕士研究生，研究方向：分布式算法。E-mail:1014115430@qq.com

*通信作者：曹飞龙(CAO Feilong)，E-mail:flcao@cjlu.edu.cn

TP391

A

0253-2395(2017)04-0661-09