浅谈高考中离心率问题的三大题型

■福建省龙岩市永定区城关中学 童其林(特级教师)

求圆锥曲线的离心率或取值范围问题是一类较为常见的问题,也经常出现在历年高考试题中。不少同学在处理离心率的取值范围问题时,常常无从下手,不知道确定参数范围的函数关系或不等关系从何而来。下面通过一些实例介绍圆锥曲线的离心率的求法,及离心率取值范围问题形成的几个背景及相应的解法,期望对同学们有所帮助。

一、求离心率的值

关键是找到含有a、b、c的一个等式,可借助图形、圆锥曲线定义或常见结论等知识寻求解决问题的突破口。

图1

点评:(1)画图很重要,要做对题,最好先画图。(2)此题图形有点复杂,关键是要找到关于a、b、c的一个等式,需要沉着冷静,胆大心细。

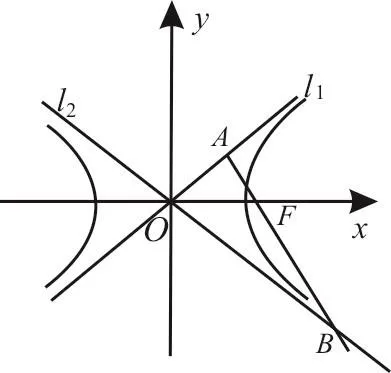
图2

点评:求离心率有很多种方法,对本题而言,利用角度的关系,可快速沟通知识模块之间的联系。

已知F1、F2是双曲线1(a＞0,b＞0)的左、右焦点,若双曲线左支上存在一点P与点F2关于直线y=对称,

则该双曲线的离心率为____。

点评:虽然思路明确,但运算量较大。

解法2：因为点P与点F2关于直线y=对称,所以FP被直2x垂直平分,交于A点。如图3,可得t a nθ+|O A|2=c2,解得|A F2|=b,|O A|=a。

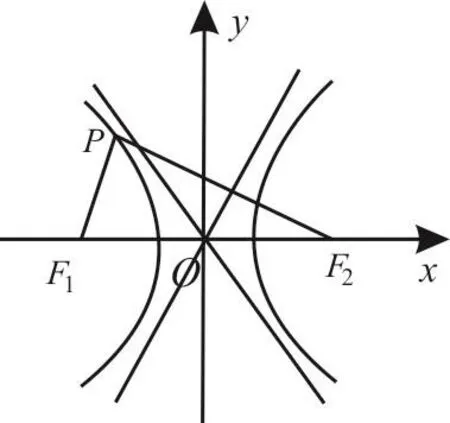
图3

又O A为△F2P F1的中位线,所以|P F1|=2|O A|=2a,|P F2|=2|A F2|=2b。

由双曲线定义可得|P F2|-|P F1|=2a,所以2b-2a=2a,b=2a,故b2=4a2。因此,c2-a2=4a2,c2=5a2

图4

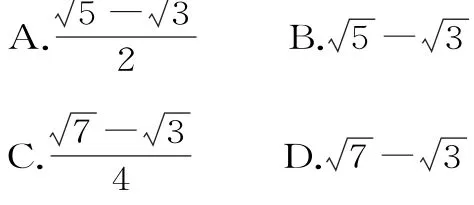
如图4,圆O的方程为x2+y2=a2,设P点坐标为(x0,y0),则圆O的切线P F2的方程为x0x+y0y=a2。又切线过点F2(c,0),所以

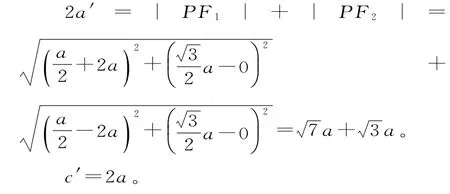
二、求离心率的范围或最值

1.利用题目所给的条件

利用题设条件能沟通所求参数与曲线上点的坐标或曲线的特征参数之间的联系,建立不等式或不等式组求解。

·kMA2

＜2,则双曲线C的离心率的取值范围为( )。

解析：由题设知A1(-a,0),A2(a,0)。假设M点坐标为(x,y),当点M在x轴上时,满足kMA1·kMA2

＜2。

当点M不在x轴上时,满足:

2.利用已知变量的范围

利用题中给出的某个已知变量的范围,或由已知条件求出某个变量的范围,然后找出这个变量与欲求的参变量之间的关系,进而求解。

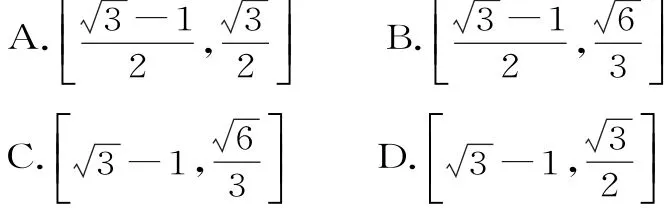
解析：如图5,因为B 和A 关于原点对称,,所以点B 也在椭圆上。

图5

O是R t△A B F的斜边中点,且|O F|=c,故|A B|=2c。

又|A F|=2cs i nα,②|B F|=2cc o sα,③

把②③代入①,得2cs i nα+2cc o sα=2a。

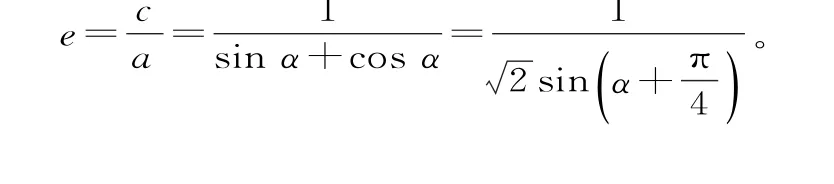
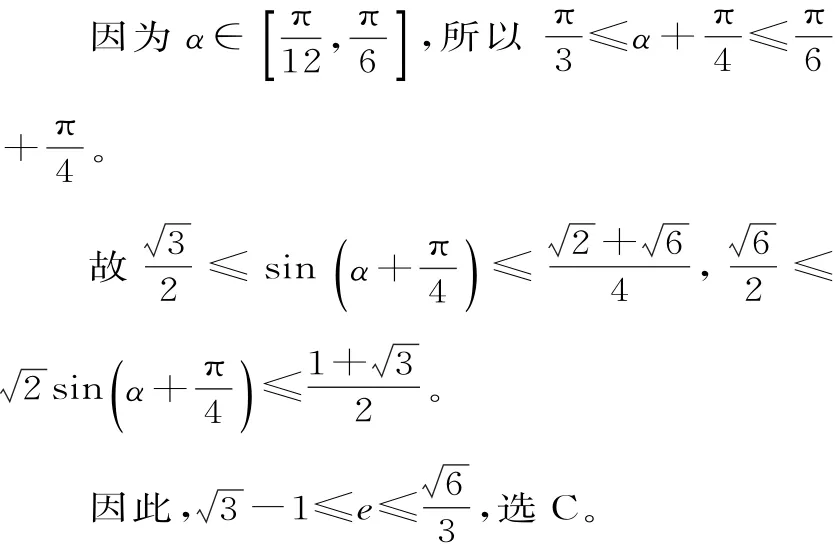
点评:本题把椭圆的定义、几何性质、解三角形,以及三角恒等变换都派上了用场,可见完成一个较复杂问题的解答过程需要全方位的知识运用。

3.利用曲线自身的取值范围

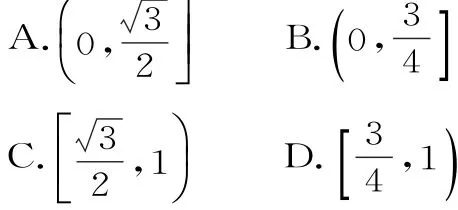
解析：如图6,设椭圆的左焦点为F1,半焦距为c,连接A F1,B F1,则四边形A F1B F为平行四边形,所以|A F1|+|B F1|=|A F|+|B F|=4。

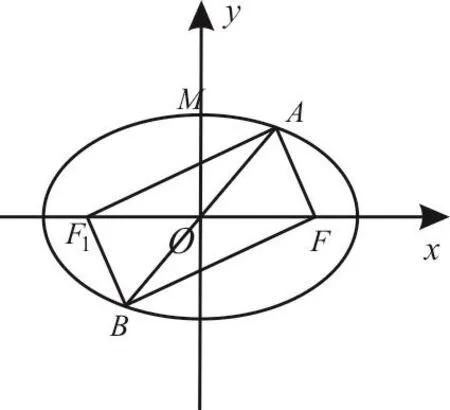
图6

根据椭圆定义知:

|A F1|+|A F|+|B F1|+|B F|=4a。所以4a=8,a=2。因为点M到直线l的距离不小于所以椭圆的离心率的取值范围为

点评:此题重点考查同学们的等价转化与化归的能力,由|A F|+|B F|=4需要推出|A F|+|A F1|=2a,另一方面要重视图形对解题的引领作用。

4.利用二次方程有解的前提条件

判断直线和圆锥曲线的关系是解析几何中最常见的题型,它们联立消元后所得的判别式为非负值是直线和圆锥曲线有公共点的充要条件。若有限制条件,则还应考虑根的分布情况,这是确定参数取值范围的一个常见条件。

解析：设点F2坐标为(c,0)。由于F2关于直线P F1的对称点M恰在y轴上,不妨设M在正半轴上,由对称性可得,|MF1|=|F1F2|=2c,且|MF1|=|MF2|,故∠MF1F2=6 0°,∠P F1F2=3 0°。

1入双曲线方程得:

(3b2-a2)x2-2c a2x-a2c2-3a2b2=0。

因为方程有两个异号的实数根,所以3b2

点评:取值范围问题,要寻找满足题设的不等式,不等式从何而来?要结合图形分析,要挖掘隐含条件。由于本题的直线P F1与双曲线恒有两个交点,这两个交点在原点的两边,即关于x的二次方程的两个根一正一负,所以只需满足两根之积小于0,问题便得以解决。

5.利用图形的位置关系

三、与离心率交汇的其他问题

对这类问题要注意全方位、多角度地去思考,寻求多种途径,尽可能通过分析推理得出最简便的方法。

解法1：如图7,设|P F1|=r1,|P F2|=r2(r1＞r2),|F1F2|=2c,椭圆的长半轴长为a1,双曲线的实半轴长为a2,椭圆、双曲线的离心率分别为e1、e2。

由余弦定理得:

解法2：如图7,设|P F1|=r1,|P F2|=r2(r1＞r2),|F1F2|=2c,椭圆的长半轴长为a1,双曲线的实半轴长为a2,椭圆、双曲线的离心率分别为e1、e2。

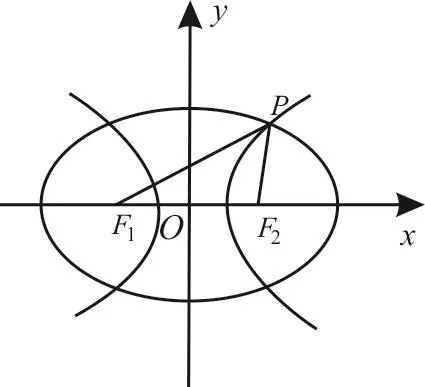
图7

解法3：如图7,设|P F1|=r1,|P F2|=r2(r1＞r2),|F1F2|=2c,椭圆的长半轴长为a1,双曲线的实半轴长为a2,椭圆、双曲线的离心率分别为e1、e2。

由余弦定理得4c2=r21+r22-r1r2=(r1+r2)2-3r1r2=4a21-3r1r2,所以e12=

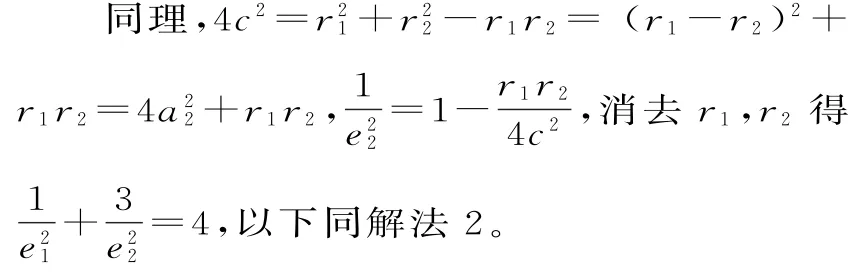
解法4：如图7,设|P F1|=r1,|P F2|=r2(r1＞r2),|F1F2|=2c,椭圆的长半轴长为a1,双曲线的实半轴长为a2,椭圆、双曲线的离心率分别为e1、e2。

解法5：如图7,设|P F1|=r1,|P F2|=r2(r1＞r2),|F1F2|=2c,椭圆的长半轴长为a1,短半轴长为b1;双曲线的实半轴长为a2,虚半轴长为b2,椭圆、双曲线的离心率分别为e1、e2。

点评:以“形”入手,借助函数、柯西不等式、三角函数、焦点三角形面积公式等,都是为了有效地架起已知与求解之间的桥梁,意在考查同学们利用知识,等价转化问题,解决问题的能力。

总之,求圆锥曲线的离心率及取值范围要抓住一个关键,两个切入点,三个方向,四种工具,五种思想。

一个关键:寻找,寻求建立a、b、c(或a、b、c中的两个)的一个等式或不等式;

两个切入点:从“形”入手,从“数”下手;

三个方向:从圆锥曲线的定义思考,从几何图形的性质出发,从方程(或不等式)的角度落笔;

四种工具:平面几何基础知识,平面向量的知识,三角函数的运用,柯西不等式;

五种思想:数形结合的思想,方程思想,函数思想,等价转化思想,分类讨论思想。

(责任编辑 徐利杰)