推陈出新巧设置 简约之中见思维

广东省广州市第一一三中学(510000)　余雪娇

1　试题呈现

(广州卷第23题)已知抛物线y1=−x2+mx+n,直线y2=kx+b,y1的对称轴与y2交于点A(−1,5),点A与y1的顶点B的距离是4.

(1)求y1的解析式;

(2)若y2随着x的增大而增大,且y1与y2都经过x轴上的同一点,求y2的解析式.

2　特色解读

2.1　题目简洁而不简单,凸显核心知识和数学方法

本题位于第23题(全卷25题),是一道中等题.措词干脆利落,不拖泥带水,不绕圈,体现简约的唯美.题型特征为求一次、二次函数的解析式,指向明确,给学生与亲切感,体现命题者对学生的人文关怀.但区区59字(不含解析式)的题目却融合函数的核心知识和初中阶段的重要数学方法.是实实在在的函数题,有别于伪函数.它考察了二次函数的顶点坐标、对称轴;二次函数图像与坐标轴的交点;两函数图像的交点;函数图像的性质;绝对值的性质;坐标与线段的转化;待定系数法求函数解析式.还涉及到数形结合,分类讨论思想,化归思想.有机的将函数与方程(方程组)知识板块相结合.涵盖了多个主干知识,同时关注了知识间的纵横联系,从不同维度考察学生的数学素养.可谓是小题目,大世界.

2.2　常规题小变化,求同存异有新意

求函数解析式是函数的常规题型.大部分题目是直接给定点坐标,然后代入求解.本题在常规中力求变化,在异中现新意.围绕求解析式,在核心知识处巧妙设置条件“y1的对称轴与y2交于点A(−1,5)”.由于对称轴为直线根据交点的含义:点在图像上,则满足解析式,建立=1,求出m,找到解题的突破口.再由点A与y1顶点B的距离是4,利用点坐标与线段的转化关系,求出n,解决第(1)小问.题干的两个条件与二次函数的对称轴、顶点相关联,旨在考查学生运用核心知识的能力.第(2)小问“y1与y2都经过x轴上的同一点”这提法与题干“y1的对称轴与y2交于点A(−1,5)”表面上看显然不同,但本质上是相同的,均是交点的问题.有些学生在审题上出错,认为是:恒过定点问题.只是提法上的一个变化,让题目有了区分度,这不得不让人叹服.另外,直线与抛物线,抛物线(直线)与坐标轴的这两类交点问题,如果是独立的考查,学生非常熟悉.而命题者却将抛物线、直线、x轴的交点揉在一块.这种变化需要学生具备分解题目的能力.首先确定是求y1与x轴的交点(两个);其次判断y2经过y1与x轴的交点是没有指定哪个点,所以就产生了分类;最后进行选择.能够充分考察学生分析问、,化归问题、解决问题的能力.一个常规题经过小小的变化,就充满浓浓的数学味,就能把学生综合能力考察出来.独具匠心!

2.3　不同解法,彰显学生不同的思维品质

解(1)由A(−1,5)在y1的对称轴上,得m=−2,顶点B(−1,n+1)

思路(一)AB=4,得|1+n−5|=4解得n=8或n=0.

思路 (二)AB=4,A(−1,5)画图,所以B(−1,9)或B(−1,1),即1+n=9或1,解得n=8或0.

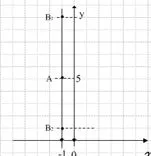
图1

(2)解设y1与x轴交于点C、D(C在D的左侧)

思路(一)当y1=−x2−2x时,解得C(−2,0),D(0,0)若y2过C点则,得y2=5x+10;若y2经过D点,则得y2=−5x.因为y2随着x的增大而增大,所以k＞0,所以y2=−5x不合题意,舍去.当y1=−x2−2x+8时类似第一种情况求解,综上y2=或y2=5x+10

思路 (二)当y1=−x2−2x时,C(−2,0),D(0,0).因为y2随着x的增大而增大,图像由左至右上升,所以如图得:y2经过D点时不合题意舍去若y2经过C点则所以y2=5x+10;当y1=−x2−2x+8时类似第一种情况把草图画出求解综上y2=或y2=5x+10

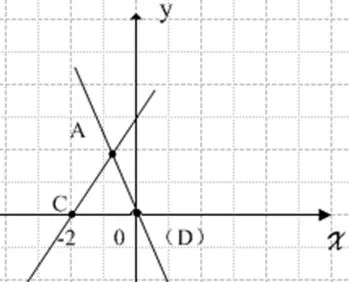
图2

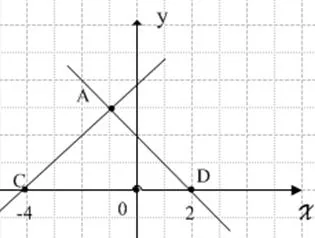
图3

第(1)小问的解法一,抓住坐标与线段的关系,用坐标的绝对值表示线段,具有抽象思维特征,是思维较高层次活动的体现.分类的标准是绝对值的性质,有效的避免漏解现象.解法二,通过画图,把B点坐标具体化,体现几何直观、数形结合思想.其分类的标准是B在A的上方还是下方,即位置.式子简单,运算量少.同时考查思维的慎密性,若考虑不全面会漏掉其中一种情况.

第(2)小问解法一,把“y2随x的增大而增大”转化为k＞0(数),需要4次解方程组求出k值,才能判断符合题意的解,过程繁琐、运算量大,耗时.解法二,直接转化为图像由左至右上升(形),画出草图,可舍去不合题意的情况,只需2次解方程组,优化解法,提高解题效率,体现数形结合的魅力.

不同的解法,体现学生不同的思维品质.不同思维层次的学生会有不同的表现,凸显思维品质的考查.能用快捷、准确的方法去完成任务的红利是省时,为后面的压轴题赢得时间,挣到主动权.从某种意义上来说这题实现了选拔、区分的功能.

3　教学导向分析

3.1　关注教学过程,回归数学本质

《课标》在实施建议中提出:学生掌握数学知识,不能依赖死记硬背,而应该理解为基础,教师应该揭示知识的数学实质及其体现的数学思想等.在现实的教学,教师容易重视结果而忽视数学思维活动过程,往往简单的向学生介绍概念或定理,然后例题讲解,再应用.“一个定义,三项注意,几道例题,大量练习”的模式,学生只会囫囵吞枣的记忆和生搬硬套的应用.学生并没有理解透彻知识的本质,谈何灵活运用?例如本题如果学生只会套用求解析式的模式:一设,二代,三求解,根本就不管用;如果只会死记硬背“k大于零时,y随x的增大而增大”充其量只会蒙个选择题;如果只会列方程组求交点坐标,而不懂交点含义,就无法找到解题突破口.函数是初中阶段的核心内容,可以纯代数,也可与几何相联系,题型变化无穷.但本人认为只要抓住本质,以不变应万变.在平面直角坐标系中函数最核心的东西就是:坐标与点的对应关系.坐标是数,点是形,借数定形,由形导数.这种转化要达到炉火纯青的程度,功在平时.例如研究一次函数的图像性质,有些教师直接告诉学生:一次函数的图像是条直线,然后再让学生取两个点画图像.这种直奔结论的教学,学生是不可能领会数学知识的本质.学生只有经历列表、描点画图像才能明白自变量、函数值到有序对到图像上的点相互依存:解析式⇔坐标(x,y)⇔点⇔图像.为了更好的理解,还可以设计如下的问题.

问题1:解析式确定,可以求图像上的点的坐标吗?怎么求?

问题2:图像上的点坐标与解析式有何关系呢,知道了点坐标可求解析式吗?

学生在深刻理解函数中数与形的关系后,待定系数法求解析式;直线与坐标轴的交点坐标;函数与方程的联系等内容就不费吹灰之力.在此基础上,增加一条直线,就有了两条直线的交点坐标;函数与方程组的联系;两点间的距离与坐标关系,图形的周长与面积等.这种关注过程的教学,让学生洞悉本质,适当的整合教材内容,系统的、整体的、联系的学,可以培养学生思维的深刻性,广阔性,灵活性,也可以提高学生的解题能力和应变能力.本题的实质:无非就是两点间的距离及线的交点的问题.掌握函数本质内容,就迎刃而解.而那种仅限于下结论,再套例题,最后归纳步骤的教学.只会培养固定题型的熟练工,缺乏对数学知识本质思考,思维定势,无法变通.

3.2　重视数形结合,培养学生画图能力

数形结合是中学教学数学中最重要的思想之一.它是连接数学中具体问题与抽象问题间的纽带.不仅可以开拓解题思路,而且使可一些数学问题变得简单易懂.例如本题只要画出草图,就能直观、准确、快速地求解.现在很多学生惧怕无图题.据近几年中考(广州市)得分统计,发现2014年平均分为历史最低,原因是填空题,极少给出图,严重影响到学生的答题时间和答题命中率.这种现状当然跟时下盛行的导学案有很大关系.导学案的图已经画好,步骤设计好,学生一步一步的填空,被牵着鼻子走到了结论,充满着伪探究.导学案极少有空白,极少有思考的空间.长久以往,学生只有被动的接受和简单的模仿.不愿动脑不愿动笔画图,思维越来越僵化.习惯有图的题目,结果是:对于几何题目,图感差,线条多时抽不出有用的图形;图形少就不会补.对于代数来说,凭空乱写一通,无法找到切入点.平时教学中教师有意识地抹去图或设计一些动态问题,引起图形变化,要求学生先画图再解决问题.例如:直角坐标系中,点O是坐标原点,四边形OABC是矩形,点A、C的坐标分别为(3,0),(0,1),点D是线段BC上的动点(与端点B、C不重合),过点D作直线y=−x+b交折线OAB于点E.记△ODE的面积为S,求S与b的函数关系式.

教学中只有不断渗透数形结合才能提高学生的画图意识.只有平时让学生多在草稿纸上反复勾勒,不断比较、深入思考,才能提高作图能力.才能消除无图带来的不适感;才能借助图形,避繁就简,找到好的解题思路.数学家华罗庚曾经说过:数形结合百般好,割裂分家万事休.