构造纠缠目击的一般方法∗
杨莹曹怀信
1)(陕西师范大学数学与信息科学学院,西安 710119)
2)(运城学院数学与信息技术学院,运城 044000)
1 引 言
随着量子理论与信息科学的交叉融合,量子信息理论成为物理学、信息科学及数学等领域的研究者共同关注的研究热点.大部分量子信息处理任务都需要一个共同的物理资源,即量子纠缠.因此,对量子信息处理任务的研究在某种程度上可以说是对量子纠缠的研究.量子纠缠作为量子通信和量子计算的载体,已被广泛用于量子计算、量子隐形传态[1]、量子密码术[2]、量子容错计算[3]、量子超密编码[4]、量子秘密共享[5]、量子安全直接通信[6]和分布式量子机器学习[7]等领域.这显示了量子纠缠的强大功能和作用.例如:Deng等[8]提出了量子超纠缠并研究了它在量子信息处理中的应用;丛美艳等[9]研究了在不同初态下Dzyaloshinskii-Moriya相互作用及内禀退相干对海森伯系统的量子纠缠的影响;任宝藏和邓富国[10]介绍了光子系统两自由度量子态在量子信息中的一些新应用,包括超并行量子计算、超纠缠态分析、超纠缠浓缩和纯化三个部分;宗晓岚和杨名[11]提出了一种可以保护多粒子纠缠不受振幅衰减影响的有效物理方案.尽管量子纠缠有如此广泛的应用,但是如何来判断给定量子纠缠性问题仍是一项相当有难度的任务[12].有一种类型的纠缠判据——纠缠目击,是探测纠缠的有效的工具,并且也是迄今为止在实验中探测纠缠最有效的工具.因此,人们对纠缠目击进行了大量的研究.例如,考虑它们的可分解性与优化问题[13,14];对局域测量纠缠目击的优化设置[15,16]以及在刻画纠缠中的应用[17−19].特别是文献[20]研究了如何使用稳定子理论构造纠缠的充分条件,提出了针对图态的纠缠目击的构造方法.文献[21—26]从另一个不同的观点说明线性规划是构造纠缠目击的一个非常有用的方法.从理论上而言,对于每一个纠缠态,至少存在一个纠缠目击来探测它.然而,如何具体构造纠缠目击仍是一个非常重要的问题.
近年来,人们试图通过机器学习理论与技术研究量子纠缠问题.随着深度学习技术在量子多体系统中的应用,通过量子纠缠透镜出现了一种新的深度学习方式,纠缠量化了机器学习中真实数据集的复杂性,可以指导人工神经网络体系的结构设计[27].Deng等[28]通过随机采样RBM的权重参数,进一步考察了一般RBM态的纠缠特性,证明了RBM能够找到具有远距离相互作用的模型哈密顿量的基态(带幂律纠缠).Levine等[29]在题为《深度学习与量子纠缠》的研究中提出了由深度卷积算法电路实现的函数和量子多体波函数之间的等价性,以期通过量子纠缠度量来量化深层网络模拟输入的复杂关联结构的能力.Carleo等[30]提出了基于神经网络的量子态表示方案,并展示了它在多个经典量子多体问题上的高精度和表达能力.Gao和Duan[31]发现深度神经网络和量子多体问题存在紧密关联,证明了利用深度神经网络模型可以有效表示几乎所有多体量子系统的波函数,展示了神经网络和深度学习算法在量子多体问题研究中的巨大潜力.
受文献[20]的启发,本文首先提出构造纠缠目击的一般方法,然后将这种构造方法应用于图态,得到相应的结论,并将这些结论与文献[20]中给出的纠缠目击进行比较,发现文献[20]中已给出的纠缠目击是本文给出的一般纠缠目击的特例,这说明本文构造的纠缠目击更具一般性.
2 纠缠目击的构造
考虑复合系统H(n):=H1⊗H2⊗………⊗Hn,用L(H(n))表示H(n)上线性算子之集;B(H(n))表示H(n)上有界线性算子之集;Bher(H(n))表示H(n)上自伴算子之集;S(H(n))表示H(n)上纯态之集;D(H(n))表示H(n)上混合态之集.
下面给出完全可分态和纠缠态的定义.
定义1[20]1)若复合量子系统H(n)上的n体纯态可以表示为分量子系统Hi上的态的张量积,即

2)复合量子系统H(n)上的n体混合态ρ可以表示为分量子系统Hk上的态的张量积的凸组合,即则称ρ是完全可分态,否则为纠缠态.

P表示H(n)上全体完全可分纯态之集;Dsep(H(n))表示H(n)上完全可分混合态之集.容易证明:Dsep(H(n))是P的闭凸包.
定义2[20]设W ∈Bher(H(n)),若
1)对任意的ρ∈Dsep(H(n)),有tr(Wρ)>0;2)存在ρ0∈D(H(n)),使得tr(Wρ0)<0,则称W为纠缠目击.
设W是一个纠缠目击,则当tr(Wρ)<0时,ρ一定是纠缠态.这时,称态ρ可被W探测.
理论上每一个纠缠态都至少存在一个纠缠目击来探测它.事实上,纠缠目击的构造并不是一件容易的事情.因此,纠缠目击的构造成为大家关注的热点问题.下面我们给出构造纠缠目击的一般方法.
一般来说,若A∈Bher(H(n)),ρ∈D(H(n)),则

其中λmin(A),λmax(A)分别为A的最小特征值与最大特征值.事实上,由于A=A †,则A有谱分解从而于是,对任量子态有所以

另外,对于给定的A∈Bher(H(n)),令

于是,有CA6λmax(A).
当CA <λmax(A)时,我们给出构造纠缠目击的一般方法.
定理1设A∈Bher(H(n)),λmax(A)为A的最大特征值,且CA6C<λmax(A),则
1)WC=CI−A是纠缠目击;
3)当ρ ∈D(H(n))满足条件Aρ=λρ(C< λ)时,WC可以探测ρ.
证明1)当ρ∈P时,由CA的定义知

从而,当ρ完全可分时,tr(WC ρ)>0.设A的最大特征值λmax(A)所对应的特征态为则

可见,WC是纠缠目击且可以探测
2) 当存在|ψ〉∈ S(H(n))使得(C< λ)时,有

3)当ρ ∈ D(H(n))满足Aρ=λρ(C< λ)时,有

可见,ρ是纠缠态且可以被WC探测.
注1由定理1知:
1)介于C与λmax(A)之间的所有特征值λ(C< λ6λmax(A)) 所对应的特征态都是纠缠的,并且这些纠缠态都可以被WC=CI−A(CA6C<λmax(A))探测到.
2)由WC探测到的那些纠缠态进行凸组合后得到的混合态也是纠缠的,并且仍然可以由WC探测到.
3)对于某些自伴算子A,确实存在ρ∈D(H(n))满足Aρ=λρ(C< λ). 例如,当A有两个特征态满足条件

时,令

则Aρ=λρ.
4)若自伴算子A的特征值λ所对应的特征态都是可分态,则称此λ为可分特征值,否则称为纠缠特征值.如图1,在数轴上,可分特征值λs都分布在CA的左侧,即λs6CA.若存在一个纠缠特征值λe满足CA < λe6λmax(A),则λe右边的所有特征值都是纠缠特征值.但是CA的左侧有可能存在纠缠特征值.例如,若A=X⊗X(X为Pauli阵),则λmin(A)=−1,λmax(A)=1,于是−1 6CA6 1.因为


其中所以特征值λmin(A)=−1位于CA的左侧,但是它所对应的特征态与都是纠缠的.这说明CA的左侧有可能存在纠缠特征值.

图1 可分特征值与部分纠缠特征值的分布示意图Fig.1.Distribution schematic of separable eigenvalues and entangled eigenvalues.
注2设W是纠缠目击,且f(ρ)<0,其中f(ρ):=tr(Wρ)(ρ∈D(H(n)))是连续函数,从而存在δ>0,使得∀σ∈D(H(n)),当时,有f(σ)<0,从而σ是纠缠态.因此如果W可以探测ρ,那么W也可以探测到ρ周围的纠缠态σ.
容易看出:对于给定的纠缠目击W和它能探测的纠缠态ρ,δ的取法并不唯一.特别地,我们可以给出δ的一个取法,取当时,有f(σ)<0,从而σ是纠缠态.事实上,可由
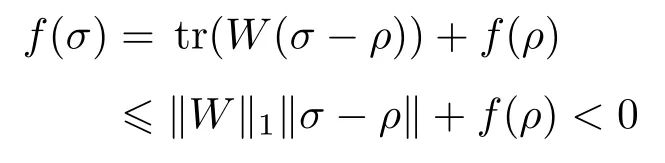
对于不同的纠缠目击,它们探测到的量子态会有所不同.下面我们由纠缠目击探测到的量子态之集给出较优纠缠目击的定义.
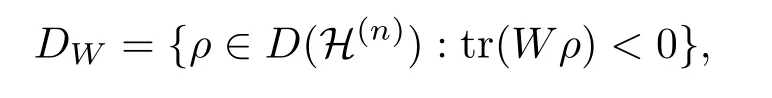
给定纠缠目击W.令即纠缠目击W所能探测到的所有量子态.
定义3[13]设W1,W2是纠缠目击,若DW2⊆DW1,则称W1比W2优.
定义4[13]设W是纠缠目击,若没有其他纠缠目击比W优,则称W是最优纠缠目击.
引理1[13]设W1,W2是纠缠目击,W1比W2优当且仅当存在正数ε和不为0的正算子P使得W2=(1− ε)W1+εP.
在定理1中,当CA6C<λmax(A)时,WC=CI−A(C是参数)是一类纠缠目击,对于这类纠缠目击,很容易得到较优的纠缠目击.
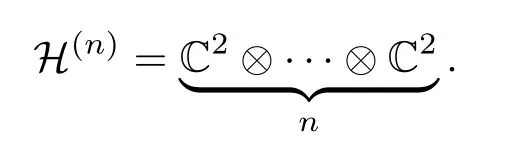
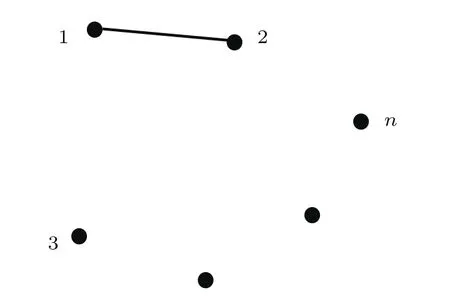
定理2设A∈Bher(H(n)),λmax(A)为A的最大特征值,且CA 证明利用引理1,要证WCA优于WC,只需要证存在正数ε和不为0的正算子P使得 因为WC=CI−A,WCA=CA I−A,所以将WC与WCA代入(1)式得 要使P是正算子,只需要因此,取 有WC=(1−ε)WCA+εP.从而,由引理1知,当CA 注3定理2表明:在形如WC=CI−A(CA6C<λmax(A))(C是参数)的纠缠目击中,WCA是最优纠缠目击,即对于任意的C(CA 注4由定理1知:介于CA与λmax(A)之间的所有特征值λ(CA < λ6λmax(A))所对应的特征态|ψ〉都是纠缠的,并且这些纠缠态都可以由WCA探测到.但是WC(CA 注5若纠缠目击WC ,WCA(CA 时,纠缠目击WC可以探测到满足此条件的纠缠态σ,而当 时,纠缠目击WCA可以探测到满足此条件的纠缠态σ.计算可得 因为CA 从而 这说明WCA探测到ρ周围的态比WC探测到ρ周围的态多.这又从另一方面说明了WCA优于WC. 注6虽然WCA探测到的态比WC多,但是在具体问题中,计算CA的精确值是特别困难的,而估计CA的范围是比较容易的,那么我们可以退而求其次,构造纠缠目击WC. 图态,顾名思义,是一类可以通过数学图形以简洁直观并且有效的方式进行刻画的特殊量子纠缠态.图态的描述方式不同,与之相对应的定义方式也不尽相同.下面给出图态的稳定化算子形式的定义. 定义5[32]设V是一个有限集,E是V的二元素子集,称G=(V,E)是一个(无向有限)图.并且V中的元素称为图G的顶点,V称为图G的顶点集,常用{1,2,………,n}表示.E中的元素可以视为连接相应顶点的边,且E称为图G的边集.对于顶点i∈V,用N(i)表示与顶点i相连的顶点之集,称为i的邻域. 若H(n)为Hilbert空间C2的n重张量积,即 对2阶矩阵T1,T2,………,Tn(视为Hilbert空间上的线性算子),用表示它们的张量积(H(n)上的算子),即 特别是当Ti=T,Tj=I(j̸=i)时,将张量积算子简记为T(i).例如,当X,Z为Pauli矩阵: 时,有其中I为2阶单位阵.显然,对任意的i,j,Z(i)与Z(j)可交换:Z(i)Z(j)=Z(j)Z(i),且X(i)与X(j)可交换:X(i)X(j)=X(j)X(i). 当i̸=j时,X(i)与Z(j)可交换:X(i)Z(j)=Z(j)X(i).这就保证了下面的算子Si定义合理. 定义6[32]给定一个图G=(V,E),顶点个数即V的元素个数为n,对该图的任意一个顶点i,定义算子 其中,当N(i)=∅时,规定Si=X(i);并称S1,S2,………,Sn为图G=(V,E)的稳定化算子. 注7由定义6可知:∀i,j∈V,有[Si ,Sj]=0. 定义7[32]给定一个具有n个顶点的图G=(V,E),称满足条件 的n-体态为图G=(V,E)的图态. 可以证明[33]:图态存在且唯一,其解析式为 其中 由此可得:如图2,具有n个顶点的空图(任意两点都不相连)所对应的图态为如图3,具有n个顶点的图中只有1,2顶点相连,此图所对应的图态为 其中 定义8[32]给定一个具有n个顶点的图G=(V,E),由稳定化算子S1,S2,………,Sn生成的交换群 称为图G=(V,E)的稳定子. 图2 空图Fig.2.Empty graph. 图3 只有1,2顶点相连的图Fig.3.A graph connected by a 1,2 vertex. 注8有2n个元素,可以表示为 其中 其中Ij是V的子集, 注9[32]可以证明 给定一个具有n个顶点的图G=(V,E),Si(i=1,2,………,n)为图G的稳定化算子,为图G的稳定子,为图G的图态.下面探讨图态的纠缠目击的构造.着重讨论使用稳定子的元素构造一类纠缠目击来探测图态周围的纠缠态.这类纠缠目击我们称为稳定子目击. 若在定理1中取A为中的某一个元素图态能被形如的纠缠目击探测吗? 我们构造的纠缠目击是基于满足条件CA6C< λmax(A)的C的存在性.若CA=λmax(A),则不存在满足条件的C,也就构造不了WC.例如:当时,由于A是自伴算子,且它的最大特征值λmax(A)=1,相应的特征态为所以CA6 1.由注8知,可设其中取的特征值为1的特征态为容易计算 因此CA=λmax(A). 于是,满足CA6C< λmax(A)的C不存在,可知图态不能被形如的纠缠目击探测. 若在定理1中取A为中任意两个元素做线性组合以后得到的算子,情况会如何呢?也就是图态能被形如WC的纠缠目击探测吗?为了简单起见,不妨取由于讨论的需要,给出下面的定义与结论. 定义9[20]设自伴算子 若K(i)L(i)=L(i)K(i)(∀i=1,2,………,n),则称K与L是局域交换的. 在一般的图G=(V,E)中,相连的两个顶点所对应的稳定化算子不是局域交换的,不相连的两个顶点所对应的稳定化算子是局域交换的.因此,对于一般的图G=(V,E)来说,可能是局域交换的,也可能不是局域交换的.例如,在图4中,S1与S2是局域交换的,S1与S3不是局域交换的. 图4 图GFig.4.GraphG. 注10由定义可知:与是局域交换的,当且仅当对任一k=1,2,………,n,要么要么中至少有一个为I. 引理2[20]两个自伴算子 是局域交换的,当且仅当K和L有一组共同的纯的乘积特征态构成空间H(n)的基. 因此CA=λmax(A)=2.但是当不是局域交换时,结果有所不同.可得如下结论. 推论1设 是一个纠缠目击,能探测图态|G〉〈G|. 证明由注8知,可设 由于 因此,∀k=1,2,………,我们有 特别地, 注11由推论1知,若不是局域交换的,则图态及其周围态能被形如的纠缠目击探测.例如,令 容易计算tr(WC ρ)=C−2<0.因此,纠缠目击能探测量子态 进一步,可以构造更一般的态 其中−1 6ai6 1(i=1,2),a1+a2>C.类似可证:纠缠目击能探测量子态ρ′. 推论2设A=Si+Sj,且Si与Sj不是局域交换的,则CA6 1且是一个纠缠目击,且能探测图态 证明在推论1中,令若Si与Sj不是局域交换的,则图态能被形如的纠缠目击探测,其中由于Si ,Sj为图G=(V,E)的稳定化算子,所以有 若Si与Sj不是局域交换的,则顶点i与j相连,即因此当时,计算可得 从而 因此,当1 6C<2时,纠缠目击WC=CI−Si −Sj是一个纠缠目击,且能探测图态 注12在推论2中令C=1,Si=S1,则W1=I−S1−Sj为文献[20]中提到的可以探测图态的纠缠目击.而我们构造的纠缠目击WC是一类探测图态的纠缠目击,包含W1. 在定理1中取A为中任意三个元素做线性组合以后得到的算子,情况会如何呢?也就是图态能被形如WC的纠缠目击探测吗?为了简单起见,不妨取 因此CA=λmax(A)=3.于是,满足CA6C< λmax(A)的C不存在,可知图态不能被形如的纠缠目击探测.但是当不是两两局域交换时,结果有所不同,可得如下结论. 推论3设 证明由注8知,可设 推论4设且Si与Sj不是局域交换的,则CA6 1且是一个纠缠目击,且能探测图态 证明在推论3中,令Si Sj.由于Si ,Sj为图G的稳定化算子,有 若Si与Sj不是局域交换的,则顶点i与j相连,即{i,j}∈E,因此j∈N(i),i∈N(j).从而 其中N(i)∆N(j)=N(i)∪N(j)− N(i)∩N(j).于是,容易得出Si ,Sj ,Si Sj不是两两局域交换的.由推论3得,CA <3且WC=CI−Si −Sj −Si Sj(CA6C<3)是一个纠缠目击,且能探测图态另外,当时,计算可得 注13在推论4中令C=1,Si=S1,则W1=I−S1−Sj −S1Sj为文献[20]中提到的可以探测图态的纠缠目击.而我们构造的纠缠目击WC是一类探测图态的纠缠目击,包含W1. 类似地,在定理1中取A为中任意k个元素作线性组合以后得到的算子,情况会如何呢?为了简单起见,不妨取可得如下结论. 推论5设不是两两局域交换的,则CA 证明由注8知,可设 其中 由于 所以 注14由推论5知,若不是两两局域交换的,则图态及其周围态能被形如的纠缠目击探测.例如,令 容易计算 其中 注15在注14中令 推论6设且S1,S2,………,Sn不是两两局域交换的,则且当时,是一个纠缠目击,且能探测图态 证明在推论5中,令 由推论5知:CA 因此,当n−1 6C 注16由推论6可知,若图G中至少有两个顶点相连,则它所对应的图态是纠缠的,即非平凡的图对应的图态都是纠缠的. 另外,在定理1中,当A取为图G的稳定子的全部元素之和时,可得下列结论. 推论7设不是两两局域交换的,则且当2n时,是一个纠缠目击,且能探测图态 证明在推论5中,令k=2n.由推论5可知:若不是两两局域交换的,则且当时,是一个纠缠目击,且能探测图态另外,由注9可得 注17由推论7可知,当时,是一个纠缠目击,且能探测图态另外,由定理2知,在这类纠缠目击是最优纠缠目击. 本文发现:当一个可观测量A在可分纯态上的最大期望CA严格小于其最大特征值λmax(A)时,算子WC=CI−A都是一个纠缠目击,只要参数C满足条件特别地,当A由图态的一些稳定子构成时,纠缠目击WCA就是文献[20]中得到的纠缠目击.虽然WCA探测到的纠缠态比WC能探测的更多,但在具体问题中,计算CA的精确值是特别困难的,而估计CA的上界是比较容易的.因此,构造纠缠目击WC比构造WCA更加方便一些.作为应用,得到了利用稳定子构造图态的纠缠目击的一系列方法.由于我们构造的纠缠目击包含了文献[20]中给出的纠缠目击,所以具有更广泛的应用价值. [1]Bennett C H,Brassard G,Crépeau C,Jozsa R,Peres A,Wootters W K 1993Phys.Rev.Lett.70 1895 [2]Ekert A K 1991Phys.Rev.Lett.67 661 [3]Steane A 1998Rep.Prog.Phys.61 117 [4]Mattle K,Weinfurter H,Kwiat P G,Zeilinger A 1996Phys.Rev.Lett.76 4656 [5]Hillery M,Bužek V,Berthiaume A 1999Phys.Rev.A59 1829 [6]Long G L,Liu X S 2002Phys.Rev.A65 032302 [7]Sheng Y B,Zhou L 2017Sci.Bull.62 1025 [8]Deng F G,Ren B C,Li X H 2017Sci.Bull.62 46 [9]Cong M Y,Yang J,Huang Y X 2016Acta Phys.Sin.65 170301(in Chinese)[丛美艳,杨晶,黄燕霞 2016物理学报65 170301] [10]Ren B C,Deng F G 2015Acta Phys.Sin.64 160303(in Chinese)[任宝藏,邓富国 2015物理学报 64 160303] [11]Zong X L,Yang M 2016Acta Phys.Sin.65 080303(in Chinese)[宗晓岚,杨名 2016物理学报65 080303] [12]Yang F,Cong S 2011Chin.J.Quant.Elect.28 391(in Chinese)[杨霏,丛爽2011量子电子学报 28 391] [13]Lewenstein M,Kraus B,Cirac J I,Horodecki P 2000Phys.Rev.A62 052310 [14]Lewenstein M,Kraus B,Horodecki P,Cirac J I 2001Phys.Rev.A63 044304 [15]Tóth G,Gühne O 2005Phys.Rev.Lett.94 060501 [16]Gühne O,Hyllus P,Bruss D,Ekert A,Lewenstein M,Macchiavello C,Sanpera A 2002Phys.Rev.A66 062305 [17]Tóth G 2004Phys.Rev.A69 052327 [18]Brukner C,Vedral V,Zeilinger A 2006Phys.Rev.A73 012110 [19]Wu L A,Bandyopadhyay S,Sarandy M S,Lidar D A 2005Phys.Rev.A72 032309 [20]Tóth G,Gühne O 2005Phys.Rev.A72 022340 [21]Doherty A C,Parrilo P A,Spedalieri F M 2005Phys.Rev.A71 032333 [22]Vianna R O,Doherty A C 2006Phys.Rev.A74 052306 [23]Jafarizadeh M A,Rezaee M,Yagoobi S K A S 2005Phys.Rev.A72 062106 [24]Jafarizadeh M A,Rezaee M,Ahadpour S 2006Phys.Rev.A74 042335 [25]Jafarizadeh M A,Najarbashi G,Habibian H 2007Phys.Rev.A75 052326 [26]Jafarizadeh M A,Suf i ani R,Nami S,Golmohammadi M 2012Quantum.Inf.Process.11 729 [27]Cheng S,Chen J,Wang L 2017Physics46 416(in Chinese)[程嵩,陈靖,王磊 2017物理 46 416] [28]Deng D L,Li X P,Sarma S D 2017Phys.Rev.X7 021021 [29]Levine Y,Yakira D,Cohen N,Shashua A 2017 arXiv:1704.01552 [30]Carleo G,Troyer M 2017Science355 602 [31]Gao X,Duan L M 2017Nature Commun.8 662 [32]Tóth G,Gühne O,Briegel H J 2005Phys.Rev.Lett.95 120405 [33]Hein M,Eisert J,Briegel H J 2003Phys.Rev.A69 062311

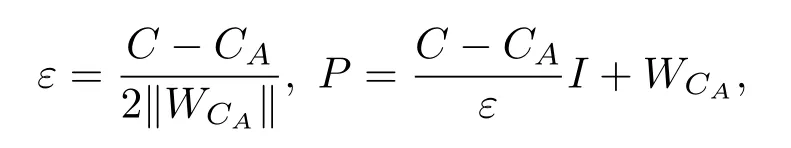





3 图态的纠缠目击的构造



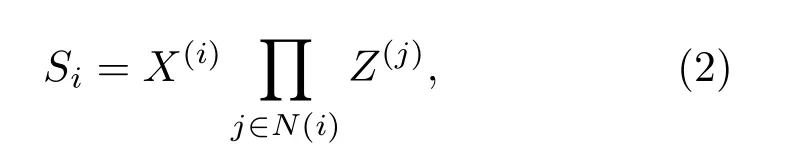


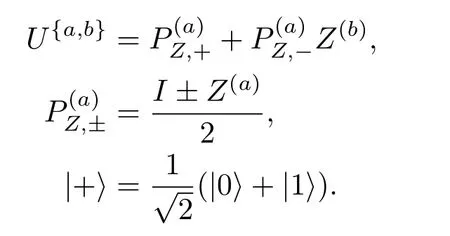
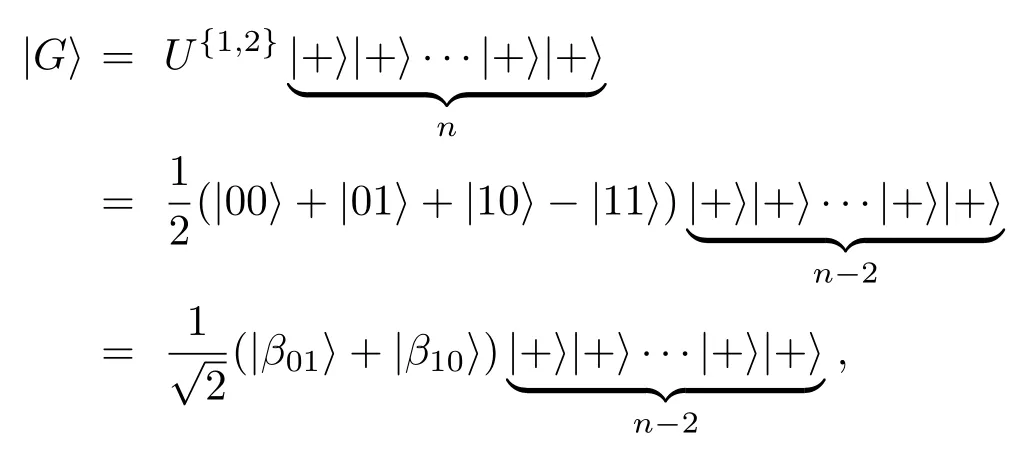
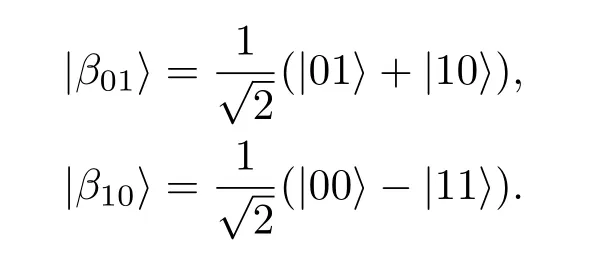
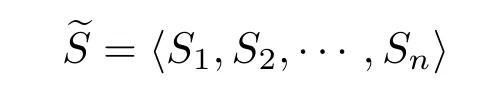

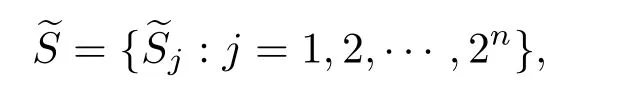

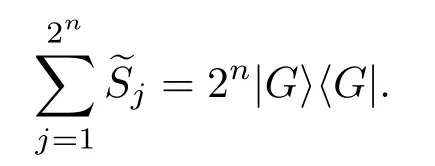






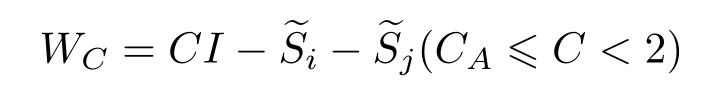














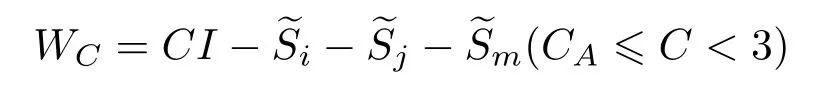
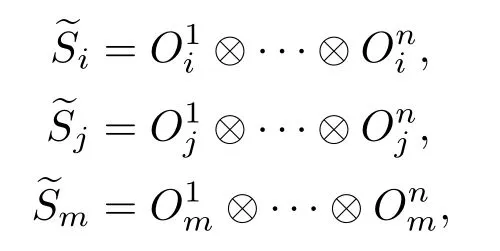

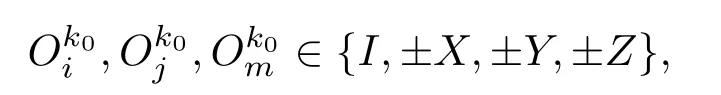
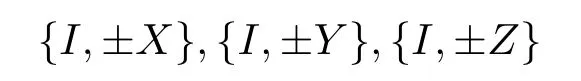

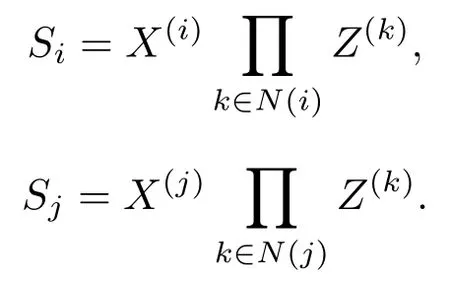




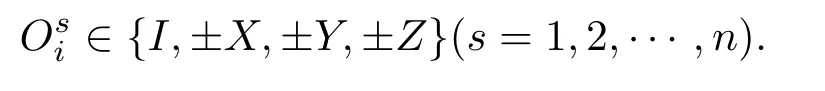


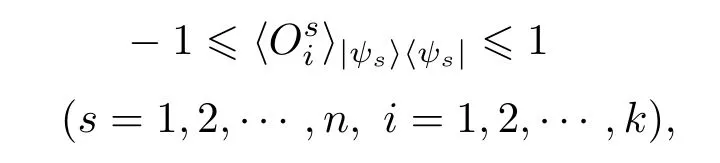
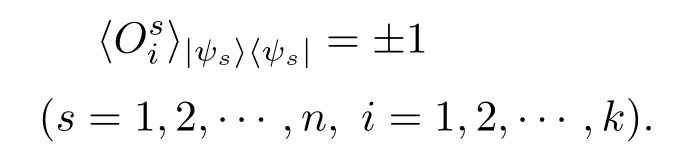









4 结 论

