由光线照球的投影谈解析几何发展数学核心素养的举措
张劲松
(人民教育出版社中学数学室 100081)
解析几何既是近现代数学的重要内容,又是高中数学课程的主干内容,历来占有重要地位.从数学分支上来说,解析几何属于几何学.几何学是研究现实世界中物体的形状、大小与位置关系的一门数学学科,解析几何是用代数方法研究几何图形的数学分支科学,研究方法是通过建立几何图形的代数方程(或不等式),运用代数运算,由代数运算的结果得到几何图形的性质.
解析几何分为平面解析几何和空间解析几何.平面解析几何主要研究直线、二次曲线以及三次以上的高次曲线,目前高中数学课程主要研究直线、圆、圆锥曲线(椭圆、双曲线和抛物线).空间解析几何以空间向量及其运算(线性运算、数量积、向量积)为工具,研究平面、直线、曲线、曲面(主要是二次曲面),建立它们的方程,用方程研究它们的性质.目前高中数学课程中不研究空间解析几何的内容.
与函数、概率、统计等数学分支相比,解析几何没有严格确定的内容,对它来说,决定性的因素不是研究对象,而是方法.解析几何的产生是科学的需要,更是方法的兴趣.开普勒发现行星沿椭圆轨道运行,物体的运动轨迹是抛物线等等,这是科学的需要.坐标系的引入,使常量数学进入变量数学时代,而变量进入数学是近代数学的重要标志.由于变量进入了数学,我们可以研究运动与变化,研究物体运动的轨迹.
对数的引入、解析几何的发明、微积分的创立被誉为17世纪自然科学的三大发现.解析几何最重要的是作为工具出现研究微积分,把图形(曲线、曲面)量化,运用微分、积分工具去研究函数的性质,因为函数用解析式(曲线)表示.作为微积分的基础,先建立函数的解析式(代数表达).运动物体的路径都是曲线,而物体本身则是由曲面界住的三维体,我们需要运用代数工具描述曲线、曲面以及三维物体.在18世纪广泛探讨二维解析几何,以及二次曲面:球面、柱面、抛物面、双叶双曲面和椭球面等.
本文首先以传统解析几何中椭圆的呈现方式为引子,通过光线照球的投影这个具体实例,阐释解析几何发展数学核心素养的举措,强调解析几何回归“几何性”的重要性,以及解析几何“解析性”与“几何性”并重的教育价值,最后对于解析几何在当前课改中面临的“最少”与“最多”的关系阐述了自己的观点.
1 传统解析几何中椭圆的呈现方式
我们以椭圆为例,看一下传统解析几何如何呈现这部分内容:
平面截圆锥,当平面与圆锥母线的角度不同时,我们可以得到椭圆、双曲线、抛物线等不同的曲线,这些曲线我们统称为圆锥曲线.
椭圆在生活中随处可见,如汽车油灌横截面的轮廓,圆柱形水杯倾斜时水面的形状,一些天体和卫星的运行轨道,都给我们以椭圆的形象.那么,椭圆具有什么几何特征呢?
如图1,取一条定长的细绳,把它的两端都固定在图板的同一点处,套上铅笔,拉紧绳子,移动笔尖,这时笔尖(动点) 画出的轨迹是一个圆.如果把细绳的两端拉开一段距离,分别固定在图板的两点处,套上铅笔,拉紧绳子,移动笔尖,笔尖满足的几何条件是什么?画出曲线的形状是什么?不断地改变两定点间的距离,感受画出的曲线的形状.
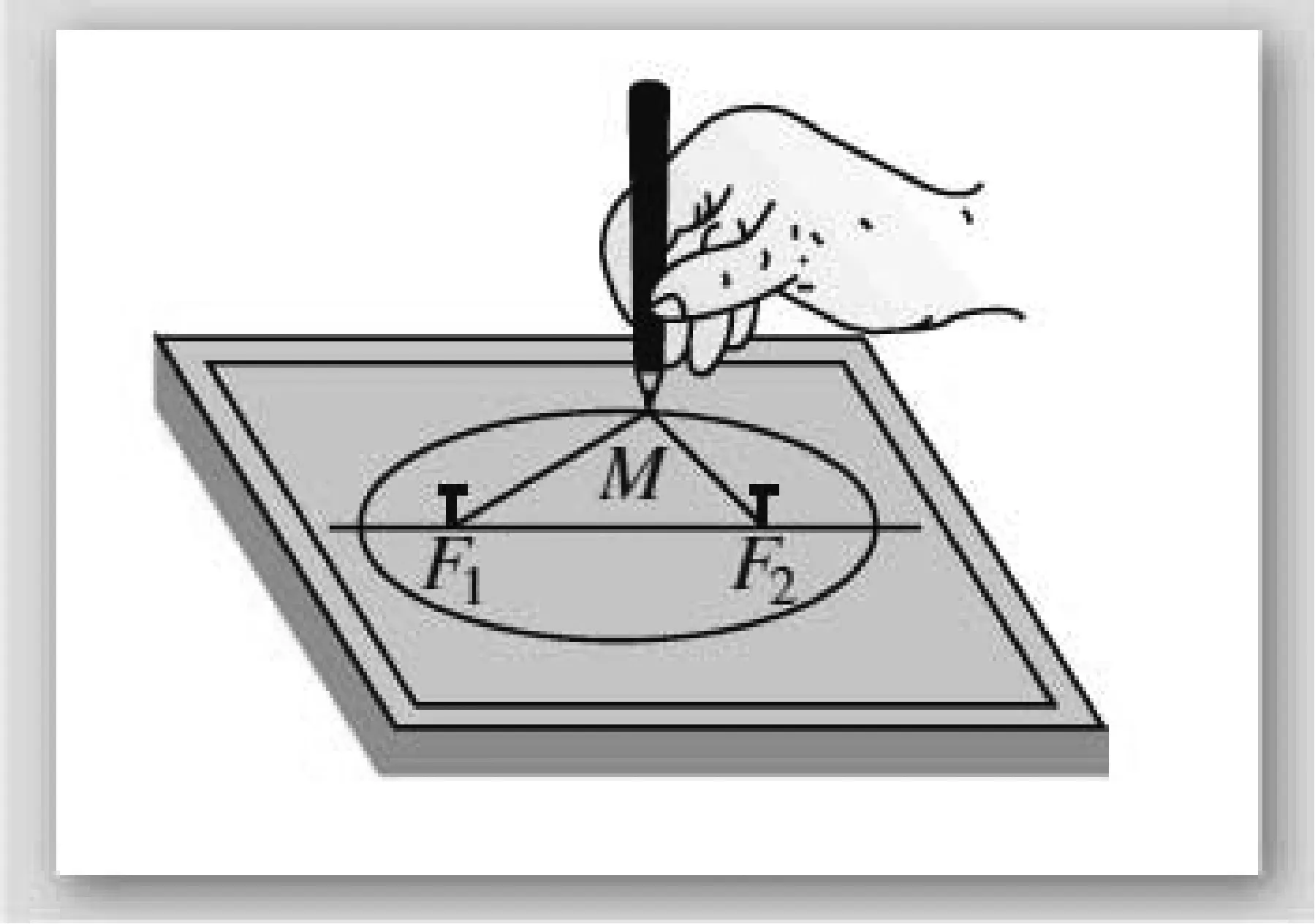
图1
通过上面具体画图的过程,我们得到,平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹,这个轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.
这是我们非常经典的呈现方式.先从平面截圆锥说起,列举生活中有大量椭圆形的物体及轨迹实例,通过椭圆画板画出椭圆,给出椭圆的定义;然后根据其对称性,建立坐标系,获得关于椭圆几何特征的代数表达式,通过数学运算,得出其标准方程,最后用其标准方程研究其范围、对称性、离心率等简单的几何性质.总之,椭圆这部分结构体系完备、内容经典条理.但是仔细阅读,我们也不难发现存在一些问题:比较集中的是几何味道明显不足,而解析味道极其浓烈,这种状况在教学中尤甚.我们需要通过呈现方式的变化做些改进.为什么这么讲,这涉及解析几何在发展数学核心素养方面的教育价值,简言之,即解析几何的“几何性”与“解析性”应并重.只有这样,解析几何的教育价值才能完全彰显.
下面,我们以光线照球的投影为例,说明解析几何回归“几何性”的重要性,以及解析几何“几何性”与“解析性”并重的教育价值.
2 光线照球的投影的本质:圆的斜投影是椭圆
光线照球的投影与旦德林双球模型是欧氏几何中非常经典的具体实例和数学模型.光线照球的投影既是探究、发现椭圆几何特征的具体实例;又是验证、加深椭圆几何特征的重要素材.椭圆是圆锥曲线的一种,而圆锥曲线是与圆锥有紧密联系的一类曲线.光线照球的投影可以看作旦德林双球模型的原型,旦德林双球模型是光线照球投影的数学模型,是对光线照球投影的数学抽象.
投影分为平行投影和中心投影,太阳光线可以看作平行投影,点光源发出的光线可以看作中心投影.如图2 是平行投影,图3是中心投影.当光线垂直于投影面照射球时,无论是平行投影还是中心投影,其投影都是圆(平行投影时投影圆的半径与球的半径相等,中心投影时投影圆的半径大于球的半径),而且球与投影圆的切点是圆的圆心.当光线不垂直于投影面照射球时,无论是平行投影还是中心投影,此时在投影面上的投影不是圆,但是与圆有天然的、紧密的联系,此时的投影是椭圆.把光线抽象为圆柱(圆锥)的母线,我们可以得到圆柱(圆锥)及其与圆柱(圆锥)侧面和投影面分别相切的球,这就是对光线照球的投影的数学抽象,即数学模型.这个数学模型的本质是:垂直于圆柱(圆锥)对称轴的截面的斜投影是椭圆.简言之,圆的斜投影是椭圆.

图2
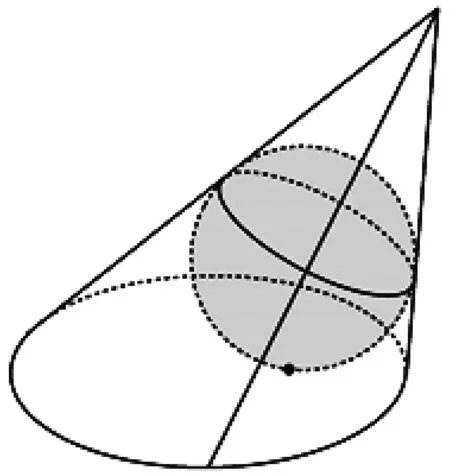
图3
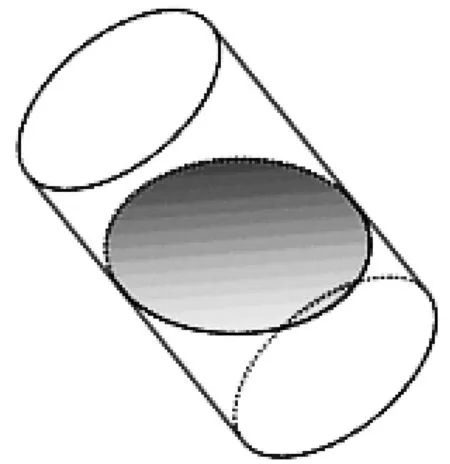
图4
现实生活中这样的具体实例或原型还有很多,如一个圆柱形水杯里的水,倾斜水杯时,原来水平的圆面变为水平的椭圆(图4).这些实例本质上是一致的,即圆的斜投影是椭圆.之所以没有直接提出“圆的斜投影是椭圆”这个命题,是因为直接证明这个命题比较困难.有了球后,不仅容易得到椭圆的焦点,而且为证明投影面是椭圆提供了证明思路.这个球在证明中起了“脚手架”的作用(后面我们会给出详细证明).
从数学的角度看,当用一个平面按上图所示的方式截圆柱(圆锥)时,所得的截面与圆柱(圆锥)侧面的交线是椭圆.这也是椭圆是圆锥曲线的由来.
圆的正投影是圆很容易证明.圆的斜投影为什么是椭圆?这是一个既现实又非常有趣的问题,会激发学生学习的兴趣和探究欲望,对于探究、发现、验证椭圆的几何特征具有积极的意义.
3 解析几何发展数学核心素养的举措:以椭圆几何特征的探究及验证为例
椭圆,顾名思义,是扁平的圆.这是形象、直观、定性地描述椭圆与圆的关系,但不是数学意义上的椭圆.
人类认识椭圆的历史非常悠久.古希腊人先是从圆柱或圆锥的截口上发现椭圆,但对椭圆几何特征的认识,经历了漫长的过程.公元3世纪,阿波罗尼斯在《圆锥曲线》中采用了截线的定义,并在多达七个命题的基础上,导出了椭圆的焦半径之和等于常数这一性质.17世纪,荷兰数学家舒腾(F. van Schooten,1615~1660)给出了椭圆的三种作图工具,其中一种利用了焦半径之和为常数的性质.法国数学家洛必达(M. de L’Hospital,1661~1704)在《圆锥曲线分析》中没有采用阿波罗尼斯的截线定义,他将椭圆定义为平面上到两定点距离之和等于常数的动点轨迹.直到1822年,比利时数学家旦德林(G. P. Dandelin,1794~1847)在一篇论文中才利用圆锥的两个内切球,直接在圆锥上导出椭圆的焦半径性质,从而证明了截面定义与轨迹定义的统一性.
历史的材料无疑是丰富的,但是追寻历史的足迹,通过展示椭圆的产生、发生和发展过程,得到目前椭圆的定义对学生来说,对教材处理来说,有很大的难度,而且对于很多教师来说,可能无法驾驭.我们想有没有一种自然的、易于接受的方式,通过探究、发现的方式认识它.不妨我们看下面的处理方式.
由于椭圆和圆分别是圆斜投影和正投影时得到的图形,我们猜想椭圆与圆肯定有天然的、紧密的联系.这个联系到底是什么?我们从圆的几何特征出发进行探究.圆的几何特征是到定点的距离等于定长的点的轨迹,圆心和半径是确定圆的几何要素,圆心(定点)确定位置,半径(定长)决定大小.由于正投影时,切点是球的投影——圆的圆心.当斜投影时球体与投影面的切点肯定也是投影图形(椭圆)的一个非常重要的点,我们猜想,这个点的地位类似圆的圆心.又由于直观发现投影图形(椭圆)的轴对称性(图5),我们猜想还有一个与其对称的点.我们设想把圆柱的侧面延长,在投影面的下方还有一个球,这个球与圆柱的侧面以及投影面都相切,显然存在另一个切点.这两个切点是非常特殊的点,投影图形与圆柱侧面的交线(椭圆)上的点与这两个切点有什么关系呢?由于圆是到定点的距离等于定长的点的轨迹,我们猜想交线上的点到两切点的距离之和为定长.这个猜想是否正确呢?通过截面以及圆的切线的性质可以证明.如图6,由圆的切线的性质知,PE=PR,PF=PQ,有PE+PF=PR+PQ=RQ,由此找到椭圆的“定长”.(圆锥情况的探索、发现及证明的思路和过程与圆柱的情况完全一致,如图7).这个交线上的点到两个切点的距离和等于定值,而这恰恰是椭圆的轨迹定义,因此这个投影是椭圆.
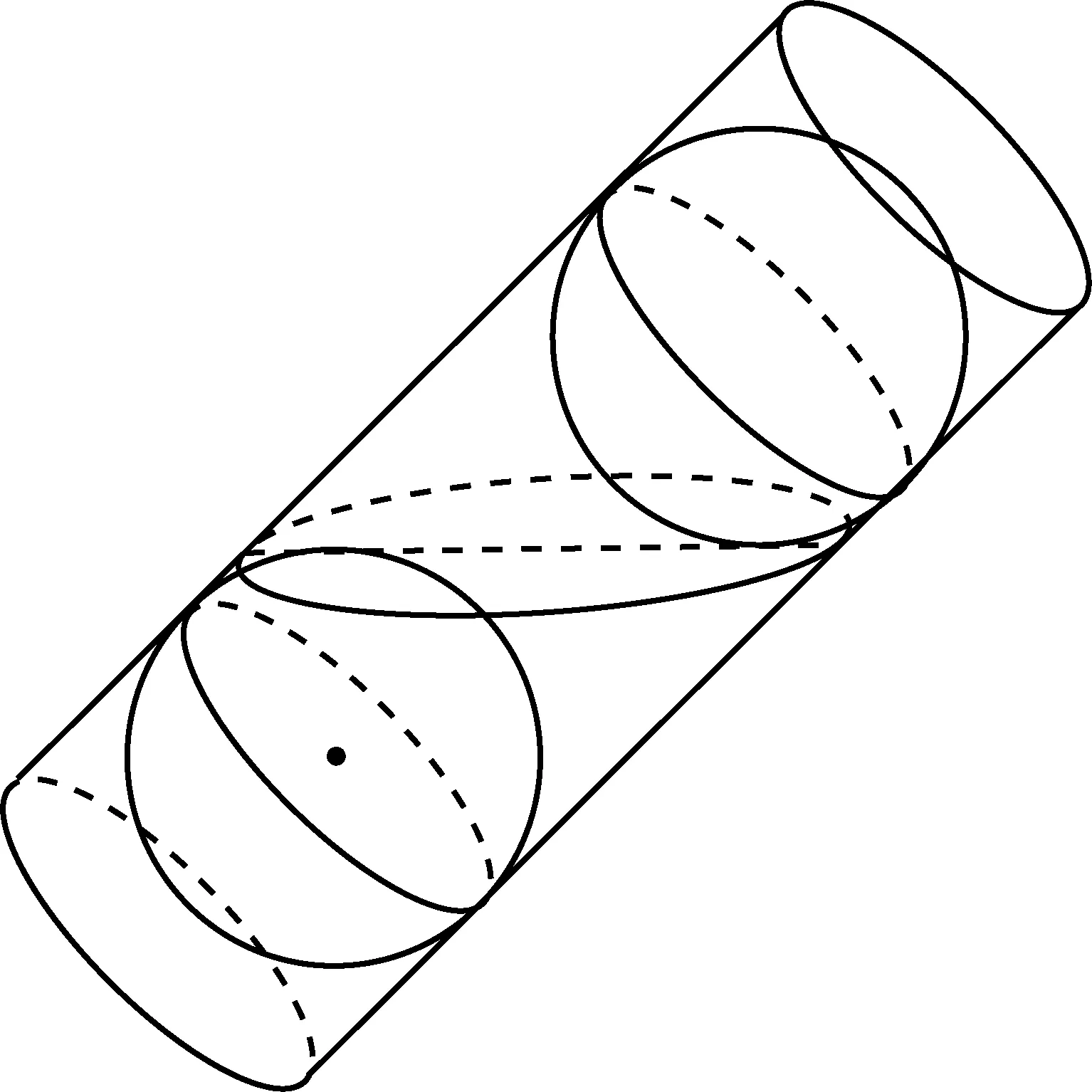
图5
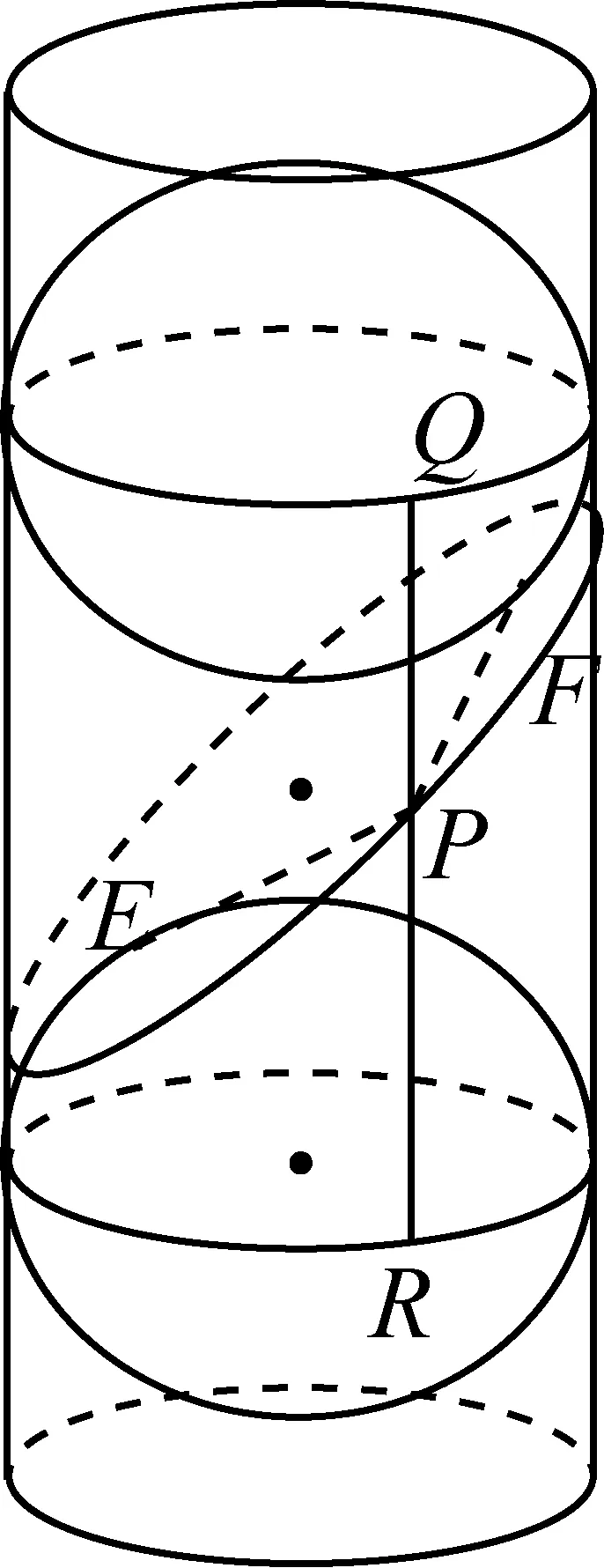
图6

图7
这样的具体实例无疑思维容量大,探索价值强.对于当前倡导的数学抽象、直观想象、逻辑推理及数学建模等数学核心素养的发展具有积极的意义.我个人认为,在当前解析几何教材编写中,这样有价值的具体实例并不多.虽然有难度,教学时间会拉长,但从长远角度讲,对于发展学生数学核心素养值得一试.
4 解析几何的教育价值:“几何性”与“解析性”并重
上述光线照球的投影的具体实例是加强椭圆内容“几何性”的一个举措,希望能在教学中进行尝试.“几何性”是指图形及图形间的关系,把握图形的形状、大小和位置关系.强调“几何性”并不排斥“解析性”,“解析性”是指建立图形的代数表达式,通过代数表达式,进行代数运算,最后把代数运算的结果“翻译”为几何结论.解析有其自身的优势,比如,要说明椭圆是扁平的圆,如何“压扁”的,解析法比综合法有优势.为此,我们完整地展现这个过程,这样对解析几何“解析性”的认识会更加深刻.
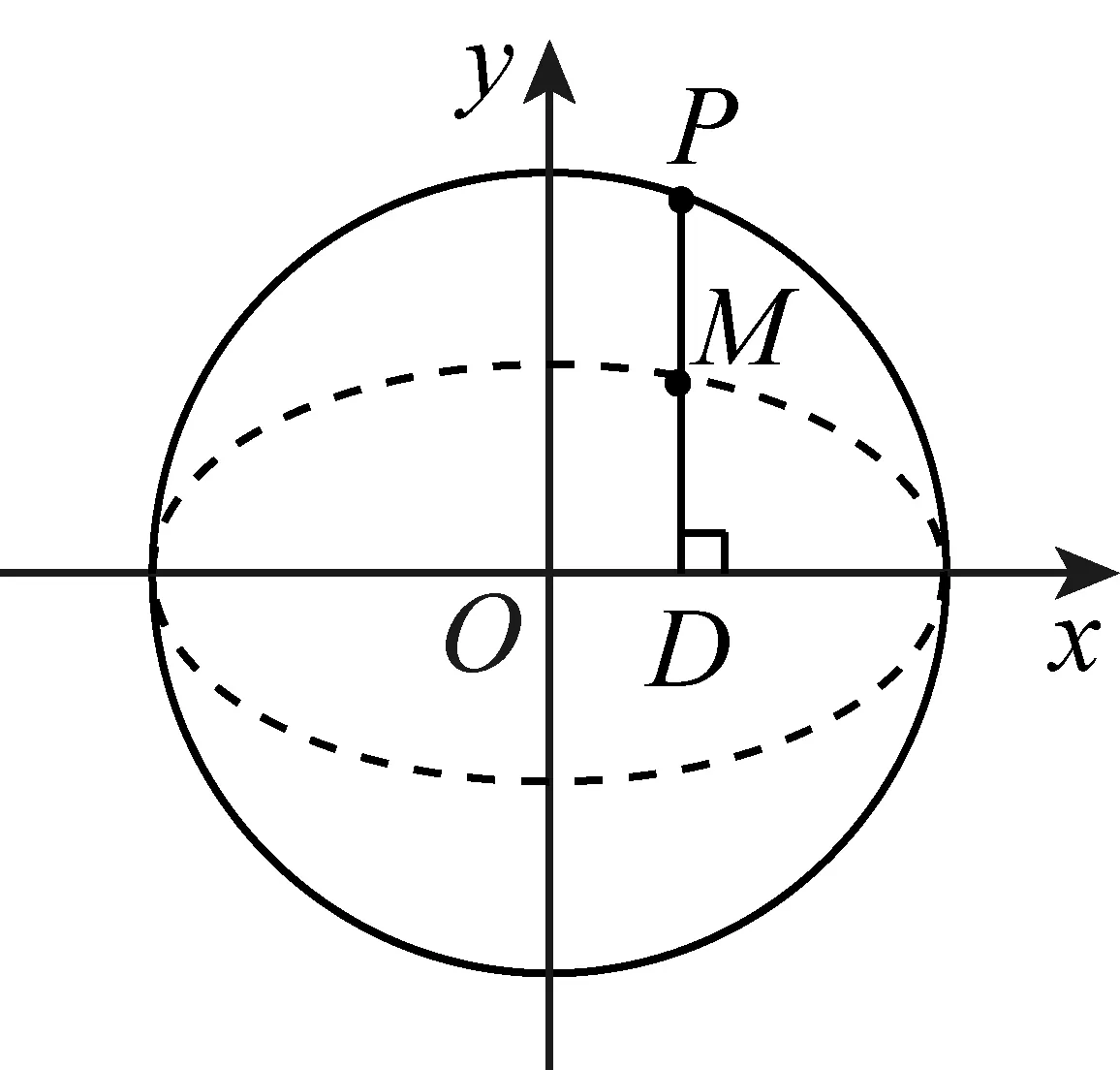
图8
问题如图8,在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是椭圆.
证明点P在圆x2+y2=4上运动,点P的运动引起点M运动.设点M的坐标为(x,y),点P的坐标为(x0,y0).由于M是线段PD的中点,所以
因为点P(x0,y0)在圆x2+y2=4上,所以

x2+4y2=4,
即

这给出如何“压扁”圆的定量描述,即把圆上任意一点的横坐标保持不变,纵坐标压缩为原来的一半,这时得到的图形是椭圆(实际上,压缩为任意比值得到的图形都是椭圆).而这用综合法证明是有难度的.
为了加强解析几何的“几何性”,除了引入圆锥曲线时,对椭圆、双曲线和抛物线的具体实例进行抽象概括外,还需挖掘一些素材,如上面提到的“光线照球的投影”;再有就是对现有的内容,如“圆锥曲线的光学性质”在教学中给予足够的重视,对性质用初等数学的方法进行说明或证明;以后有了导数的工具后,在“导数及其应用”的内容中,我们再利用切线给出严格的证明.把“解析性”运算的威力与“几何性”图形的魅力有机地结合起来.
总之,如果把解析几何看作一枚硬币,那么“几何性”与“解析性”的关系就是这枚硬币的两面,是一个整体,两者都不能偏颇.
5 如何看待“最少”与“最多”的关系
当前,我们面临的一个事实是:纵向与历史其他时期对比,当前解析几何的内容是最少的;横向与其他国家对比,我国解析几何的内容又是最多的.这个“最少”与“最多”的关系,对于我们来说,有点尴尬.但这个客观事实,需要我们重新审视解析几何的地位、作用及内容.
从平面解析几何的产生、发生和发展来看,解析几何的历史无疑是辉煌的,但是现在已经“没落”了,其内容已经进入函数、微积分、代数几何等现代数学各分支中.
平面解析几何是从初等数学过渡到高等数学的桥梁.它是用代数方法研究空间形式.它和代数中的函数知识有密切的联系,但是研究的对象不同.它所研究的对象和平面几何相同,但是研究的方法不同.从数学发展史看,过去算术是算术,代数是代数,几何是几何,数和形的研究是分开发展的.出现解析几何以后,数和形的研究紧密地结合起来,数学各分支才在更高的观点下统一起来.这样既有利于综合运用数学知识,又有利于系统掌握平面解析几何的基本知识和基本技能,为以后学习高等数学打下扎实的基础.
从平面解析几何清末初定学制时期进入课堂的变迁和发展看,解析几何的内容变化很大、但是结构体系变化不大.从总体上看,内容逐渐减少;从结构体系上看,变化极其有限,主要是解析几何的体系结构非常成熟和完整.
解析几何内容的逐渐减少源自对解析几何的教育价值、地位和作用的认识.一种观点认为,在中学学习解析几何主要是为大学继续学习数学,特别是微积分打基础.另一种观点认为,解析几何的综合性强,它综合了代数、几何、三角等知识内容,加强了代数、几何、三角等内容的联系,解析几何的代数对象是方程,对方程进行代数变形,涉及数、式、方程求解等基本代数运算;几何对象包括各种直线型图形、圆、椭圆、双曲线和抛物线等.研究方法是代数运算与几何图形性质的有机结合,包括必要的图形证明.在上述两种观点的指导下,解析几何的内容非常丰富和综合.再一种观点是,解析几何是数学的一个分支,学会解析几何的研究方法远比解析几何内容本身更重要.另外从横向角度看,其他内容如函数、统计与概率等的增加,解析几何内容需要“瘦身”“削枝强干”“腾地方“,只保留主干内容和基本的研究方法,只研究具体的曲线,不研究一般曲线及其方程;不在图形证明的难度和代数运算的复杂度上下功夫.
毋庸讳言,现在数学分支越来越多,学生数学基础的内容、内涵不断扩大,学生需要学习具备的数学基础越来越广,删减解析几何的内容,降低要求是大势所趋,如两条直线所成的角,直线的法线式方程,圆锥曲线的切线和法线,圆锥曲线的统一定义,坐标轴的平移和旋转,一般二元二次方程与曲线类型的讨论等.现在解析几何更加强调基本内容,更加突出研究方法,不在内容的深广度上做更多的拓展.
从解析几何结构体系上来说,遵循从简单到复杂,从具体到抽象,从特殊到一般的研究过程和方法.具体从几何研究对象来说,就是按照直线、圆、椭圆、双曲线、抛物线的顺序,由它们的几何特征,建立它们的方程;从方程类型上来说,先讲一般方程,后讲参数方程;从坐标系上来说,先讲直角坐标系,再讲其他坐标系,如极坐标系、柱坐标系、球坐标系等等.
作为传统或经典的数学内容,从内容上看,解析几何始终在减少,但核心内容未动;从结构上看,没有大的变化,只是有些细微的调整;从呈现形式看,注意数学内容的教材表达,以问题引导内容的展开,突出解析几何的思想和主要研究方法:如何刻画几何图形,确定图形的几何要素是什么,这些几何要素的代数表达是什么.从历史上看,方程的内容先于函数,后来函数的内容由方程内容分离出来,逐渐发展成为一个体系.与方程相比,函数有其特殊性,以函数为基础的数学分支科学的发展是近现代数学的重大成就,特别是微积分,解析几何为函数内容的产生和发展提供了重要的支撑.从数学各分支之间的关系看,解析几何更多的是一种工具,为微积分等学科服务,因为它建立了曲线与方程之间的关系,可以用代数方法精确地描述几何对象,对几何对象进行“运算”,而数形结合为数学的研究提供了工具和活力.数缺形时少直观,形少数时难入微,“直观”与“入微”的有机结合,相得益彰,极大丰富了数学研究的内容.
“最少”与“最多”的关系恰恰说明了解析几何地位、价值不断变化的过程.解析几何内容减少是大势所趋,而我国之所以“最多”的原因是多方面的,如对基础的不同理解、课程结构中重必修轻选修等等.

