一类具有饱和发生率和潜伏期的SEIR模型的稳定性*

豆中丽，王锐

(1. 重庆工商大学融智学院，重庆 400055； 2. 重庆大学数学科学学院，重庆 401331)

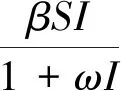
(1)

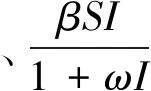
(2)

由生物学的实际意义，我们仅在区域G={(S,E,I)|S≥0,E≥0,I≥0,S+E+I≤N}中讨论模型(2)解的性态，可以验证G是模型(2)的正向不变集。

1 基本再生数和无病平衡点的稳定性

其中

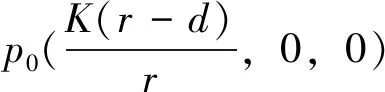
令

则

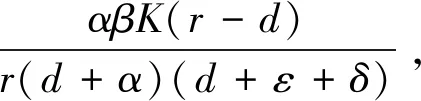
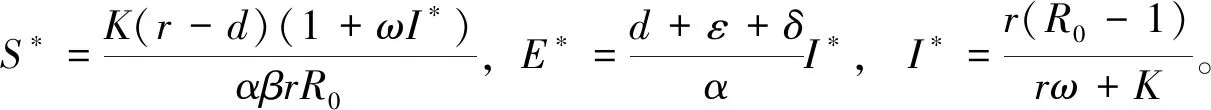
定理1 当R0<1时，模型(2)的无病平衡点p0是渐近稳定的；当R0>1时，模型(2)的无病平衡点p0是不稳定的。

证明在无病平衡点p0处线性化系统的Jacobin矩阵为：

系统的特征方程为：

[λ+(r-d)][λ2+(2d+ε+α+δ)λ+

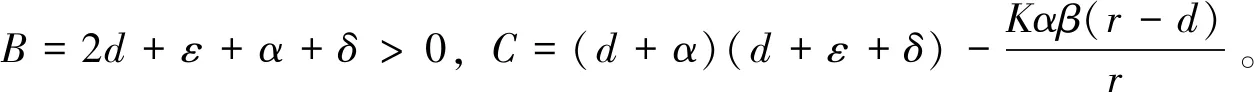
下面证明无病平衡点是全局稳定的，构造Lyapunov函数

容易验证函数V(S,E,I)是正定函数[8]，求V(S,E,I)沿着方程组(2)轨线的全导数得：

2 地方病平衡点的局部稳定性

模型(2)在地方病平衡点p*(S*,E*,I*)处的线性化系统的特征矩阵为：

J(p*)=

由于地方病平衡点解的三个分量S*,E*,I*已经表示出来，但是没有给出具体的解，所以矩阵J(p*)的特征值的实部的正负性不容易判断，利用复合矩阵进行判断一个3×3矩阵A和它的二阶加性复合矩阵A[2]为[9]：

矩阵J(p*)的二阶复合矩阵J[2](p*)为：

其中

再取D=diag(I*,E*,S*)为对角矩阵，与矩阵J[2](p*)相似矩阵DJ[2](p*)D-1为：

由R0>1得到，矩阵DJ[2](p*)D-1的对角线元素均为负数，非对角线元素均为非负数。得到矩阵DJ[2](p*)D-1每行元素之和分别为

(3)

将地方病平衡点的分量所满足的关系

(4)

代入表达式(3)后得到

再由R0>1得到h1<0,h2<0,h3<0.

这表明矩阵DJ[2](p*)D-1的所有特征值都位于复平面的左半部分，即矩DJ[2](p*)D-1的所有特征值的实部都小于零，所以矩阵DJ[2](p*)D-1稳定。

根据复合矩阵的的定理，当R0>1时，把式(4)代入直接计算

故矩阵J(p*)是稳定的，即当R0>1，模型(2)的地方病平衡点是局部渐近稳定的。

3 地方病平衡点的全局稳定性

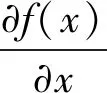
由竞争系统的理论[10]，可知模型(2)的任意非空紧集的极限集只能是周期解或者地方病平衡点，如果还能证明模型(2)有非常数周期解，就可以得到地方病平衡点的全局稳定性。

定理2 当R0>1时，若模型(2)有非常数周期解p(t)，则p(t)是渐近稳定的。

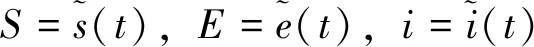
(5)

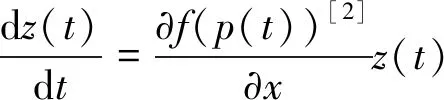
(6)

取

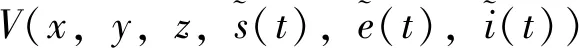
(7)

整理后可得到

其中

(8)

由方程组(2)可得到

将这两个式子带入到(7)式中，得到

由不等式

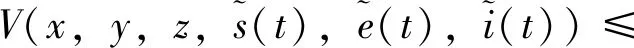
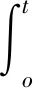
模型(2)的地方病平衡点全局渐近稳定的结论说明，地方病平衡点最后不会消失，而会趋于一个常量。

4 结 论

本文建立了具有饱和发生率和潜伏期的SEIR模型，通过计算得到模型的基本再生数R0和平衡点。当R0<1时，模型的无病平衡点p0是渐近稳定的，说明生物种群中的染病者逐渐减少并将趋于灭绝。运用复合矩阵判定定理分析了当R0>1时，地方病平衡点p*的渐近稳定性；最后利用竞争系统定理，证明了地方病平衡点的全局稳定性，说明生物种群中的疾病最终不会消失，易感者、潜伏者、染病者和恢复者在种群中的比例最后会趋于一个常量。