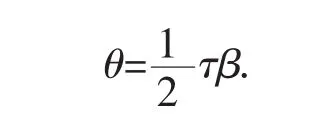局部对偶平坦的Matsumoto度量

叶 闻，耿 杰

（安徽信息工程学院 通识教育与外国语学院，安徽 芜湖241000）

Hibert第四问题［1］研究了Rn中的开集U上的Finsler度量,使得直线具有最短路径.定义在Rn中的开集U上的具有上述性质的Finsler度量称为射影平坦度量.关于射影平坦的Finsler度量目前研究的比较多,例如文［2］射影平坦的 Finsler度量，文［3］射影平坦的 Matsumoto 度量.对于对偶平坦的 Matsumoto 度量［4］,目前的结果还不是很多,具体的例子也很少.其实这类Finsler度量是几何学在神经网络、信息几何、超弦理论等领域中有重要应用的一类研究对象，所以对偶平坦的度量也引起了人们越来越多的重视.例如文［5］中给出了局部对偶平坦的Randers度量的充要条件等.本文根据局部对偶平坦Finsler度量的定义给出了这一度量为局部对偶平坦的充要条件.

1 预备知识

设F=（x,y）是开集U⊂Rn上的Finsler度量,如果F满足:

则称F是局部对偶平坦的［7-8］.

设（M,F）是n维的Finsler流形，Gi和Gαi分别是定义在F和α上的测地系数.表示为：

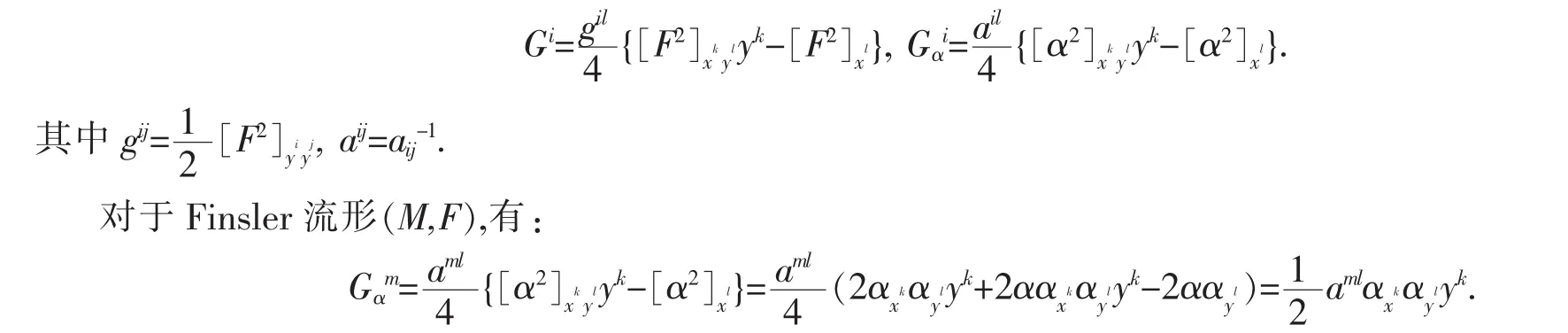
所以有：

2 主要结论

本文主要研究了局部对偶平坦的Matsumoto度量,并得出以下结果.

3 定理的证明

首先，定理的充分性是显然的，只需证明其必要性.先计算Matsumoto度量是局部对偶平坦时满足的方程.将（4），（5），（6），（7）式代入，通过计算得：

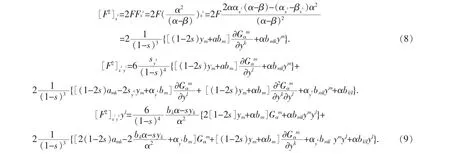
将（12），（13）式用 bk缩并［9］，然后将（14），（15）式代入得：

将（16），（17）式整理后得：

将（18）×β+（19）×α 整理后得：

因为（b2α2-β2）不能整除（α2-β2）和 α2，所以存在 τ=τ（t），使得：

将（20）式整理得：

因为α2不能被β2整除，得：

由（22）式得：

所以 θ=θkyk是 α 的射影因子.由（4），（24）式得：

将（26）式代入（23）式得：

将（22），（27）代入（21）式得：

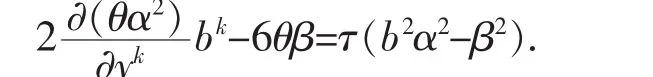
整理得：

因为 2θβ-τβ2=0 不能整除 α2，所以：

解得：