玩转外接球

黄映珊

一、直接法

如果几何体是正方体、长方体或直棱柱，则其外接球的球心可直接确定。因为对于正方体或长方体，其外接球球心在其体对角线中点的位置，直径就是体对角线。而直棱柱，其外接球球心在两底面的外接圆圆心连线的中点处。

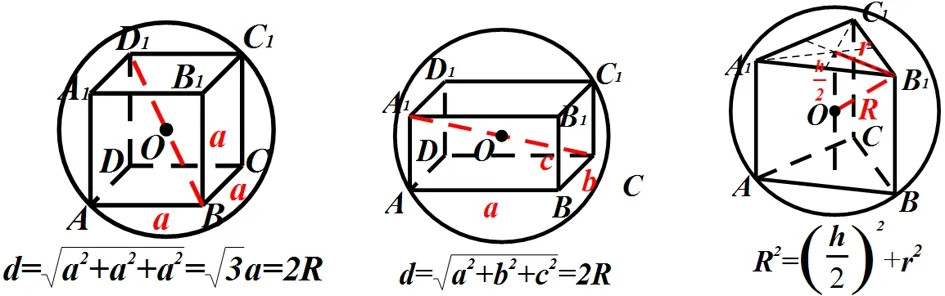
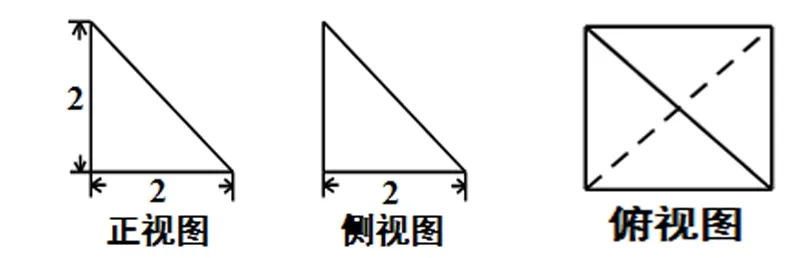
例1（16佛一模）某一简单几何体的三视图如图所示，该几何体的外接球的表面积是（ ）

A.13π B.16π

C.25π D.27π

【解析】如图所示三视图，可还原成如下几何体：

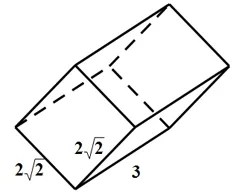
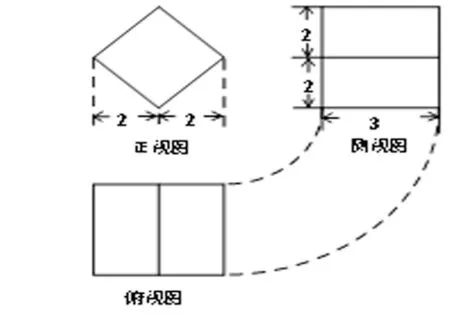
二、构造法（补形法）

对于一些垂直关系比较多，或者比较特殊的椎体，我们可以将其放入长方体、正方体或直棱柱中，即补形，从而转化为长方体、正方体、直棱柱的外接球。下面主要从常见的两种补形的几何体进行说明：

（1）构造正方体（或长方体）

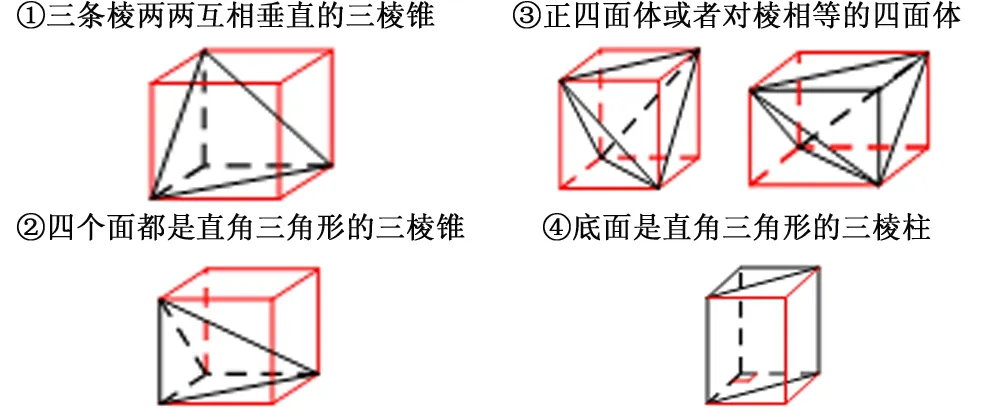
例2（17佛一模）某几何体的三视图如图所示，则该几何体的外接球的表面积为（ ）

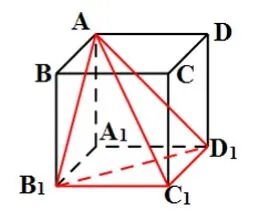
【解析】如图所示三视图，可还原成如下三棱锥A-B1C1D1：

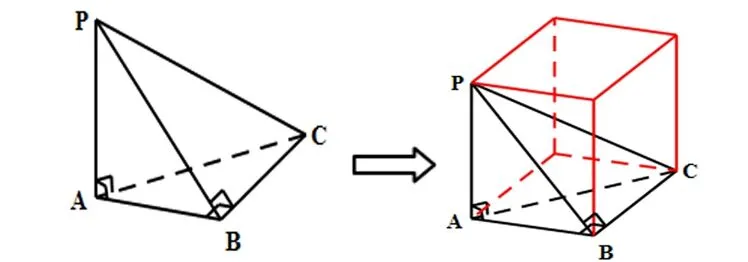
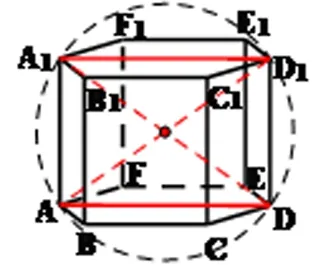
例3（17.广一模）《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称为阳马；将四个面都为直角三角形的三棱锥称之为鱉臑。若三棱锥P-ABC为鱉臑，PA⊥平面ABC，PA＝AB＝2，AC＝4，三棱锥P-ABC的四个顶点都在球O的球面上，则球O的表面积为（ ）

A.8π B.12π C.20π D.24π

【解析】根据题意可画出如左下图所示模型，并可构造成右下图所示长方体，PC为外接球直径，，半径为，表面积为S球＝4πR2＝20π，选C。

例4已知棱长为1的正四面体ABCD（四个面都是正三角形）的所有顶点都在球O的球面上，则球O的表面积为_____。

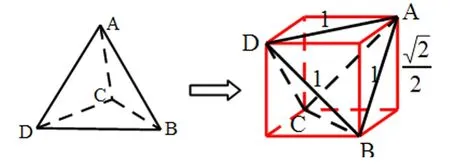
【解析】如左图所示棱长为1的正四面体ABCD，可构造成如右图所示的正方体，则正方体的边长为则外接球直径为：d＝，半径为，表面积为S球＝4πR2＝

（2）构造直三棱柱

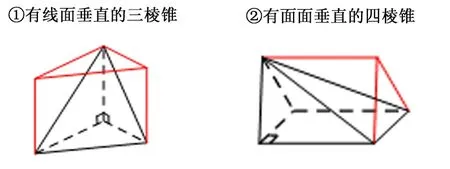
【解析】如下图所示，三棱柱P-ABC，根据PC⊥平面ABC，可构造成三棱柱ABC-DEP：

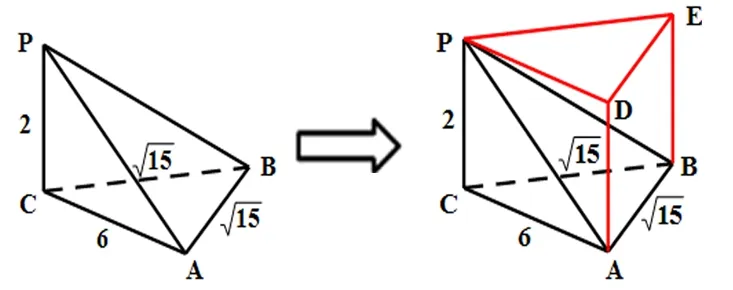
例6如图所示，已知△EAB所在的平面与矩形ABCD所在的平面互相垂直，EA＝EB＝3，AD＝2，∠AEB＝60°，则多面体E-ABCD的外接球的表面积为（ ）

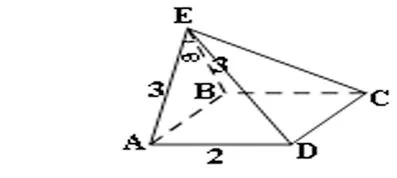
【解析】如图，由于∠AEB＝60°，所以并不好构造成长方体或正方体，可构造成如下图所示三棱柱ABE-DCF：

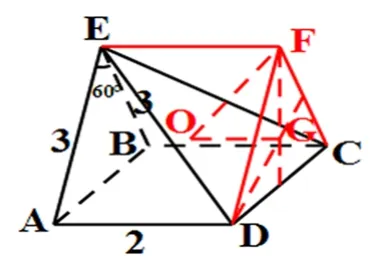
则四棱锥E-ABCD的外接球也是三棱柱ABE-DCF的外接球，球心到两底面的距离相等，为AD的一半，即OG＝1.由余弦定理可得AB2＝32+32-2×3×3cos60°＝9，所以DC＝AB＝3，△DCF的外接圆半径为，外接球半径，易得该外接球表面积为S球＝4πR2＝16π，选C。

三、轴截面法

对于正棱锥或侧棱长相等的棱锥，其外接球的球心一定在锥顶点与底面几何图形外接圆圆心的连线或其延长线上。还有正棱柱，选取适当的截面，在该平面内求出外接球半径。该方法的实质就是通过寻找外接球的一个大圆，从而把立体几何问题转化为平面几何问题来研究。

例7（16广一模）一个六棱柱的底面是正六边形，侧棱垂直于底面，所有棱的长都为1，顶点都在同一个球面上，则该球体积为（ ）

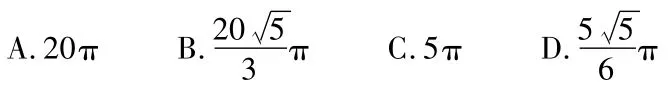
【解析】如下图六棱柱ABCDEF-A1B1C1D1E1F1，轴截面ADD1A1的外接圆就是球的大圆，其半径即为球的半径。

易得，AA1＝1，AD＝2，所以，半径为，体积为，选D。

四、性质法

球中小圆圆心与球心的连线与小圆所在平面垂直。因此，球心在过小圆圆心且垂直于小圆所在平面的直线上。如果能找到多个这样的直线，则这些直线的交点，即为球心。因此，对于不规则几何体可以先在各个面内找出平面几何图形的外接圆圆心，再过这些圆心作所在平面的垂线，找到垂线的交点即可。

【解析】如图所示四边形ABCD，沿直线AC将△ACD翻折成△ACD’，当三棱锥D’-ABC的体积取得最大时，△AD’C⊥△ABC，

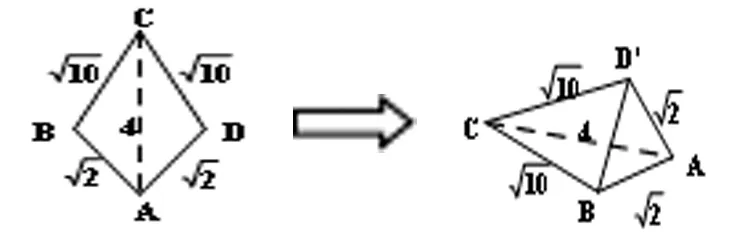
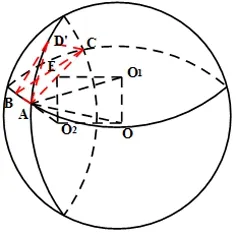
设O1是△ABC外接圆的圆心，O2是△AD’C外接圆的圆心，O为外接球的球心，则AC是两圆的公共弦，设AC的中点为E，则，且O1E⊥AC，O2E⊥AC，因为，平面AD’C⊥平面ABC，平面AD’C∩平面ABC＝AC，O1E⊂平面ABC，所以，O1E⊥平面AD’C。另外，OO2⊥平面AD’C，所以，O1E∥OO2。同理，O2E∥OO1，所以四边形OO1EO2是边长为1的正方形，OO1＝O2E＝1。在Rt△OO1A中，由勾股定理得外接球O的半径所以外接球表面积为S球＝4πR2＝24π。

例9已知球O被互相垂直的两个平面所截，得到两圆的公共弦AB长为2，若两圆的半径分别为和3，则球O的表面积为______。

【解析】球O被互相垂直的两个平面所截，设两截面的圆心分别为O1、O2，如图所示，可得取AB中点C，则BC＝1，O1C⊥AB，O2C⊥AB，易得

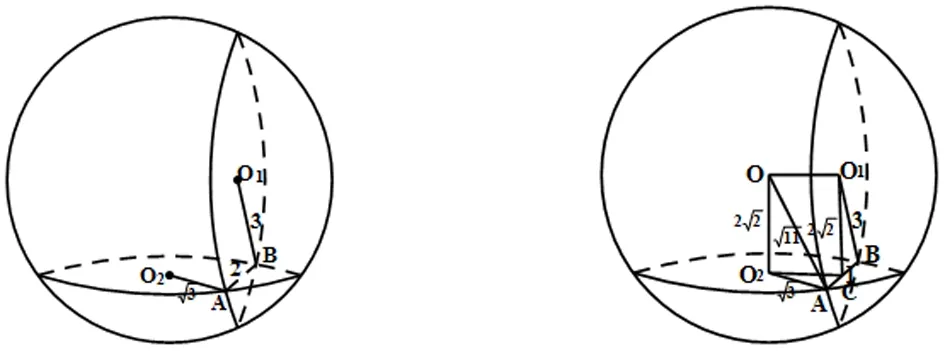
另外，OO1⊥O1C，OO2⊥O2C，则四边形OO1CO2是矩形，所以OO2＝连接OA，则△OO2A是直角三角形，OA是球O的半径，OA，所以球O的变面积为S球＝4πR2＝44π。

总之，求多面体的外接球，要特别注意多面体中的线线、线面、面面的垂直关系，以及多面体有关几何元素与球的半径之间的关系。