高考中的分段函数

杨金林

分段函数问题是高中数学中分类讨论思想的典型体现.近年来，高考对折线函数的命题常与绝对值综合考查，既考查对绝对值定义、含绝对值函数图象变换的理解，又考查与函数、方程、不等式等综合的运用，着重考查分类讨论思想在解题中运用.

一、一次函數中分段函数问题

例1 （2018年高考理新课标I卷）已知f（x）=|x+1|-|ax-1|.

（1）当a=1时，求不等式f（x）>1的解集;

（2）若x∈（0，1）时，不等式f（x）>x成立，求a的取值范围.

分析：（1）将a=1代入函数解析式，求得f（x）=|x+1|-|x-1|，利用零点分段将解析式化为f（x）=-2，x≤-1

2x，-1

2，x≥1，然后利用分段函数，分情况讨论求得不等式f（x）>1的解集为{x|x>12};

（2）根据题中所给的x∈（0，1），其中一个绝对值符号可以去掉，不等式f（x）>x可以化为x∈（0，1）时|ax-1|<1，分情况讨论即可求得结果.

解析：（1）当a=1时，f（x）=|x+1|-|x-1|，

即f（x）=-2，x≤-1

2x，-1

2，x≥1，

故不等式f（x）>1的解集为{x|x>12};

（2）当x∈（0，1）时|x+1|-|ax-1|>x成立等价于当x∈（0，1）时|ax-1|<1成立.

若a≤0，则当x∈（0，1）时|ax-1|≥1;若a>0，|ax-1|<1的解集为0

综上，a的取值范围为（0，2].

点睛：该题考查的是有关绝对值不等式的解法，以及含参的绝对值的式子在某个区间上恒成立求参数的取值范围的问题，在解题的过程中，需要会用零点分段法将其化为分段函数，从而将不等式转化为多个不等式组来解决，关于第二问求参数的取值范围时，可以应用题中所给的自变量的范围，去掉一个绝对值符号，之后进行分类讨论，求得结果.

二、二次函数中分段函数问题

例2 已知函数f（x）=|x2+3x|，x∈R.若方程f（x）-a|x-1|=0恰有4个互异的实数根，则实数a的取值范围为    .

解析：在同一坐标系中画f（x）=|x2+3x|和g（x）=a|x-1|的图象（如图），问题转化为f（x）与g（x）图象恰有四个交点.

当y=a（x-1）与y=x2+3x（或y=-a（x-1）与y=-x2-3x）相切时，f（x）与g（x）图象恰有三个交点.把y=a（x-1）代入y=x2+3x，得x2+3x=a（x-1），即x2+（3-a）x+a=0，由Δ=0，得（3-a）2-4a=0，解得a=1或a=9.又当a=0时，f（x）与g（x）仅两个交点，∴09.

三、高次函数中分段函数问题

例3 已知函数f（x）=-|x3-2x2+x|，x<1

lnx，x≥1

若对于t∈R，f（t）≤kt恒成立，则实数k的取值范围是    .

解析：①当t≥1时，f（t）=lnt，即lnt≤kt对于t∈[1，+∞）恒成立，所以k≥lntt，t∈[1，+∞）.令g（t）=lntt，则g′（t）=1-lntt2，当t∈（1，e）时，g′（t）>0，则g（t）=lntt在t∈（1，e）时为增函数;当t∈（e，+∞）时，g′（t）<0，则g（t）=lntt在t∈（e，+∞）时为减函数.所以g（t）max=g（e）=1e，所以k≥1e.

②当0

③当t≤0时，f（t）=t（t-1）2，即t（t-1）2≤kt对于t∈（-∞，0]恒成立，所以k≤（t-1）2，t∈（-∞，0]，所以k≤1.

综上，1e≤k≤1.

点睛：本题考查了分段函数、利用导数求最值，以及恒成立问题等内容，借助分类讨论使问题得到解决.本题属于难题.

四、超越函数中分段函数问题

例4 设函数f（x）=1，x=1

loga|x-1|+1，x≠1，若函数g（x）=[f（x）]2+bf（x）+c有三个零点x1，x2，x3，则x1x2+x2x3+x1x3等于    .

解析：由图可得关于x的方程f（x）=t的解有两个或三个（t=1时有三个，t≠1时有两个），所以关于t的方程t2+bt+c=0只能有一个根t=1（若有两个根，则关于x的方程[f（x）]2+bf（x）+c=0有四个或五个根），由f（x）=1，可得x1，x2，x3的值分别为0，1，2，x1x2+x2x3+x1x3=0×1+1×2+0×2=2，故答案为2.

点睛：1.本题主要考查分段函数的图象和解析式;2.函数零点与方程根之间的关系及数形结合思想的应用，属于难题.判断方程y=f（x）零点个数的常用方法：①直接法：可利用判别式的正负直接判定一元二次方程根的个数;②转化法：函数y=f（x）零点个数就是方程f（x）=0根的个数，结合函数的图象与性质（如单调性、奇偶性、周期性、对称性）可确定函数的零点个数;③数形结合法：一是转化为两个函数y=g（x），y=h（x）的图象的交点个数问题，画出两个函数的图象，其交点的个数就是函数零点的个数，二是转化为y=a，y=g（x）的交点个数的图象的交点个数问题.本题判定方程f（x）=t的根的个数就是利用了方法③.

例5 （2016年高考天津理数）已知函数f（x）=x2+（4a-3）x+3a，x<0，

loga（x+1）+1，x≥0（a>0，且a≠1）在R上单调递减，且关于x的方程|f（x）|=2-x恰好有两个不相等的實数解，则a的取值范围是（  ）

A.（0，23] B.[23，34]

C.[13，23]∪{34}D.[13，23）∪{34}

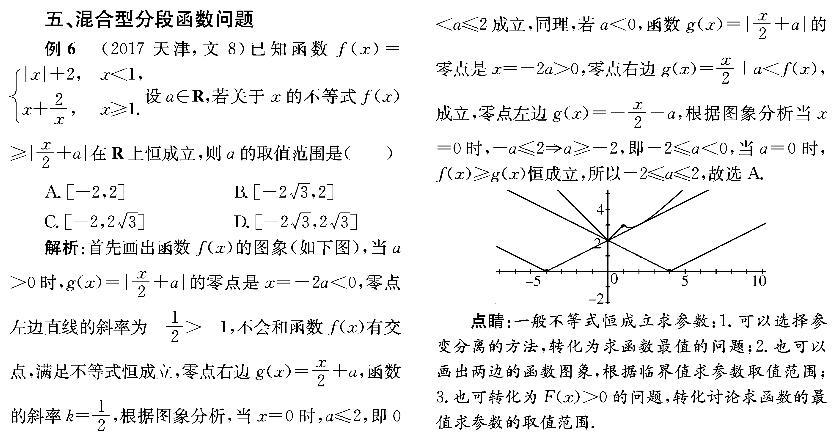
解析：法一：由y=loga（x+1）+1在[0，+∞）上递减，得0

又由f（x）在R上单调递减，

则02+（4a-3）·0+3a≥1

3-4a2≥0，解得13≤a≤34.

如图所示，在同一坐标系中

作出函数y=|f（x）|和y=2-x的图象.

由图象可知，在[0，+∞）上|f（x）|=2-x有且仅有一个解，故在（-∞，0）上|f（x）|=2-x同样有且仅有一个解.

当3a>2，即a>23时，由x2+（4a-3）x+3a=2-x（其中x<0），得x2+（4a-2）x+3a-2=0（其中x<0），则Δ=（4a-2）2-4（3a-2）=0，解得a=34或a=1（舍去）;

当1≤3a≤2，即13≤a≤23时，由图象可知，符合条件.

综上所述，a∈[13，23]∪{34}.故选C.

法二：通过比较四个选项可知，只需验证a=13，23，34是否满足即可.

当a=13时，f（x）=x2-53x+1，x<0

log13（x+1）+1，x≥0

其图象如图.显然a=13满足条件.

故排除B，用同样的方法验证a=23，a=34.故选C.

点睛：数形结合法是解题中广泛使用的一种方法，一是直接使用数形结合的方法得出问题的答案，二是根据数形结合思想得出问题满足的条件，在解答题中一般是后一种情况，在客观题中一般是前一种情况或两种情况的综合.数形结合解题的关键是把“数式”转化为“图形”，通过“图形”得出问题的答案或者找到解决问题的思路.

五、混合型分段函数问题

例6 （2017天津，文8）已知函数f（x）=|x|+2，x<1，

x+2x，x≥1.设a∈R，若关于x的不等式f（x）≥|x2+a|在R上恒成立，则a的取值范围是（  ）

A.[-2，2] B.[-23，2]

C.[-2，23] D.[-23，23]

解析：首先画出函数f（x）的图象（如下图），当a>0时，g（x）=|x2+a|的零点是x=-2a<0，零点左边直线的斜率为-12>-1，不会和函数f（x）有交点，满足不等式恒成立，零点右边g（x）=x2+a，函数的斜率k=12，根据图象分析，当x=0时，a≤2，即00，零点右边g（x）=x2+a

点睛：一般不等式恒成立求参数：1.可以选择参变分离的方法，转化为求函数最值的问题;2.也可以画出两边的函数图象，根据临界值求参数取值范围;3.也可转化为F（x）>0的问题，转化讨论求函数的最值求参数的取值范围.