脉冲发电机与直线感应电机直连供电系统建模与仿真

孙昌平，谢贤飞，于克训，易正康，张恒浩

(1. 华中科技大学电气与电子工程学院，武汉 430074； 2. 强电磁工程与新技术国家重点实验室，武汉 430074；3.中国运载火箭技术研究院研究发展部，北京100076)

1 引言

电磁发射技术是利用电磁力来发射物体的技术，具有推力大、控制精度高、成本低等优点[1-2]。其中，大功率直线电机因其推力密度高、机械结构简单、可靠性高等突出优势，在舰载机弹射器、月球物资回送等大载荷运输场合具有广阔的应用前景[3-4]。在各类直线电机中，直线感应电机由于更容易实现对动子的制动，且对电源频率要求较低[5]，因此，其应用于电磁发射领域的方案可行性更高，有较高的研究价值。

针对电磁发射这种短时大功率爆发式输出的场合，常规电源系统难以满足要求[6-7]，需要配备高功率的脉冲电源，才能有效实现大载荷的推进和加速。脉冲电源主要分为电容型、电感型和脉冲发电机型，其中，脉冲发电机具有高储能密度、高功率密度的综合优势，不只是单纯的电能存储装置，而是集储能、发电和脉冲输出于一体，可以不经整流逆变等中间环节直接对交流负载供电，是极具应用前景的电磁发射器用脉冲电源[8-10]。目前，在直线感应电机模型和供电等方面已开展了分析研究，并取得一定成果：鲁军勇等[11]搭建了高速长定子双边直线感应电机的瞬态数学模型，分析了电机的动态性能；牟树君等[12]研究了一种用于电磁发射的变极距式直线感应电机，并进行了电磁设计和性能分析；张明元等[13]对长定子直线感应电机分段供电技术进行了综述和探讨。

基于上述研究，本文将开展脉冲发电机对直线感应电机直连供电方案的研究，从供电方式、模型建立、参数变化对性能影响等方面进行分析。

2 准稳态仿真模型

2.1 供电电路

根据发射所需的功率和储能要求的不同，本文提出可采用单台脉冲发电机或多台脉冲发电机并联组合的运行方式进行供电，其电路示意图如图1所示。这种直连方式最大的优点是省掉了大功率整流逆变电路，降低了系统成本和控制复杂度，提高了供电可靠性。系统的工作过程简述为：①原动机拖动脉冲发电机达到额定转速；②各发电机依次投入并网；③闭合供电开关为直线电机供电；④发射装置达到预期发射速度后断开供电开关，结束供电。

图1 脉冲发电机-直线感应电机直联供电示意图Fig.1 Direct connection circuit of pulse generator and LIM

2.2 模型建立

在分析多电机系统时，常规的、基于瞬态电机模型的仿真方法精度较高，能够清晰地表示各个阶段电机参数变化的细节，但由于其求解速度过慢，不利于在全系统初始设计阶段对系统性能进行快速评估和优化分析，使得这种仿真方法有其局限性。为此，本文提出了采用准稳态模型进行仿真求解的分析方法，并做如下假设：①各发电机三相绕组参数对称且相等；②不考虑电机剩磁和饱和影响。

首先，以单台发电机供电系统为例阐述准稳态模型的原理。下文均采用定子1、2、0坐标系进行推导。式(1)和式(2)分别为脉冲发电机和直线感应电机在1轴下的数学模型，其中，脉冲发电机采用发电机惯例，直线感应电机采用电动机惯例。

(1)

(2)

式中：u、i、ψ、R、L分别表示电压、电流、磁链、电阻、电感，p为微分算子，β=π/τ，其中τ为直线电机极距，v表示直线电机动子速度。下标中：1代表1轴分量；G为脉冲发电机参数，M为直线电动机参数，s为定子侧，r为转子侧，d为发电机直轴，q为交轴，f为励磁，m为主电感，l为漏电感。上标“′”表示折算值，“*”表示共轭。由于在电磁发射过程中，两台电机的电磁瞬态过程远短于机械瞬态过程，忽略电磁瞬态过程，认为在较短的一段时间内，各电参量近似处于正弦稳态。设两台电机电接口处A相电压为式(3)：

uAG=uAM=Umaxcos(ωet+θu)

(3)

可以得到式(4)：

(4)

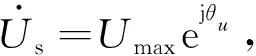
由于电路处于正弦稳态，其余各电磁参量的角频率同样为ωe，其1轴分量均可以表示为式(5)：

(5)

式中：x可取u、i、ψ；y可取sG、sM、rM。

采用相量形式表示，电机数学模型可改写为式(6)：

(6)

式中：

(7)

图2 单发电机系统准稳态等效电路Fig.2 Quasi-steady state equivalent circuit of single generator system

实际上，2台电机的准稳态电路与各自的稳态电路在形式上是一致的，其区别在于准稳态电路中的参数在仿真过程中是变化的。例如，直线电机的转差率S将随着动子速度的增大而逐渐减小，电路中的电抗参数和发电机空载电势E0将随着发电机转速的下降而逐渐减小。准稳态电路与瞬态电路的另一区别在于其忽略了从一个稳态到下一个稳态之间的瞬态过程。因此，准稳态电路可以认为是介于稳态电路与瞬态电路之间一种电路形式。

瞬态数学模型中，直线感应电机的电磁推力方程为式(8)：

(8)

准稳态模型中的对应方程为式(9)：

(9)

直线电机动子运动方程为式(10)：

(10)

式中：Fμ为动子所受的空气阻力和滑动摩擦力等阻力的合力；m1和m2分别为发射体质量和直线感应电机动子质量。

在发射过程中，发电机转速和供电频率会随着转子储能的减少而逐渐下降，两者的瞬时值可由式(11)得到：

(11)

式中：EG为发电机当前储能,EG0为初始储能,η1和η2分别为脉冲发电机和直线电机的能量效率,EoutM为直线电机输出机械能。

发电机空载电势为式(12)：

E0=4.44fN1kdp1Φ1

(12)

式中：N1为脉冲发电机定子绕组每相串联匝数,kdp1为定子基波绕组系数,Φ1为每极下基波主磁通量。当励磁电流ifG恒定时，Φ1恒定，E0仅与供电频率有关，如式(13)所示。

(13)

式中：E00为供电初始时刻即发电机最高转速时的空载电势，可由电磁场仿真或空载试验得到。

图3 N台发电机并联供电系统准稳态等效电路Fig.3 Quasi-steady state equivalent circuit of system with N generators in parallel

根据上述式(6)、(9)、(10)、(11)、(13)可搭建如图4所示的Simulink仿真模型。

图4 准稳态电路Simulink仿真模型Fig.4 Simulink model of quasi-steady state circuit

2.3 模型精确度对比分析

为校核准稳态模型的精度，需将其与瞬态仿真模型进行对比测试，瞬态仿真模型采用Simulink中S函数模块进行搭建，S函数模块按照式(1)、(2)、(8)、(10)和式(11)编写。

本文以表1所示的一组电机参数为输入，对准稳态模型和瞬态仿真模型进行了测试，并将两种模型的仿真结果进行了对比。表中PM为直线感应电机运行过程中最大输出功率。

表 1 电磁发射系统参数

图5为2种仿真模型的推力、速度和发电机转速下降率的对比图。从图5(a)可以看到，瞬态模型的电磁推力在发射初始阶段存在较大的瞬态波动过程，与准稳态模型相差较大，然而由于发射初始阶段直线电机动子速度很低，这种波动对转速变化过程的影响并不大。在图5(b)中，发射器从0加速到500 m/s所需的时间，瞬态模型为2.01 s，准稳态模型为1.97 s，相对误差为-1.99%。图5(c)中的发电机转速下降率kn可以用来表征系统效率，瞬态模型中最终转速下降率为0.910，准稳态模型为0.913，相对误差为0.33%。据此可以得到两仿真模型系统效率的相对误差为3.29%。

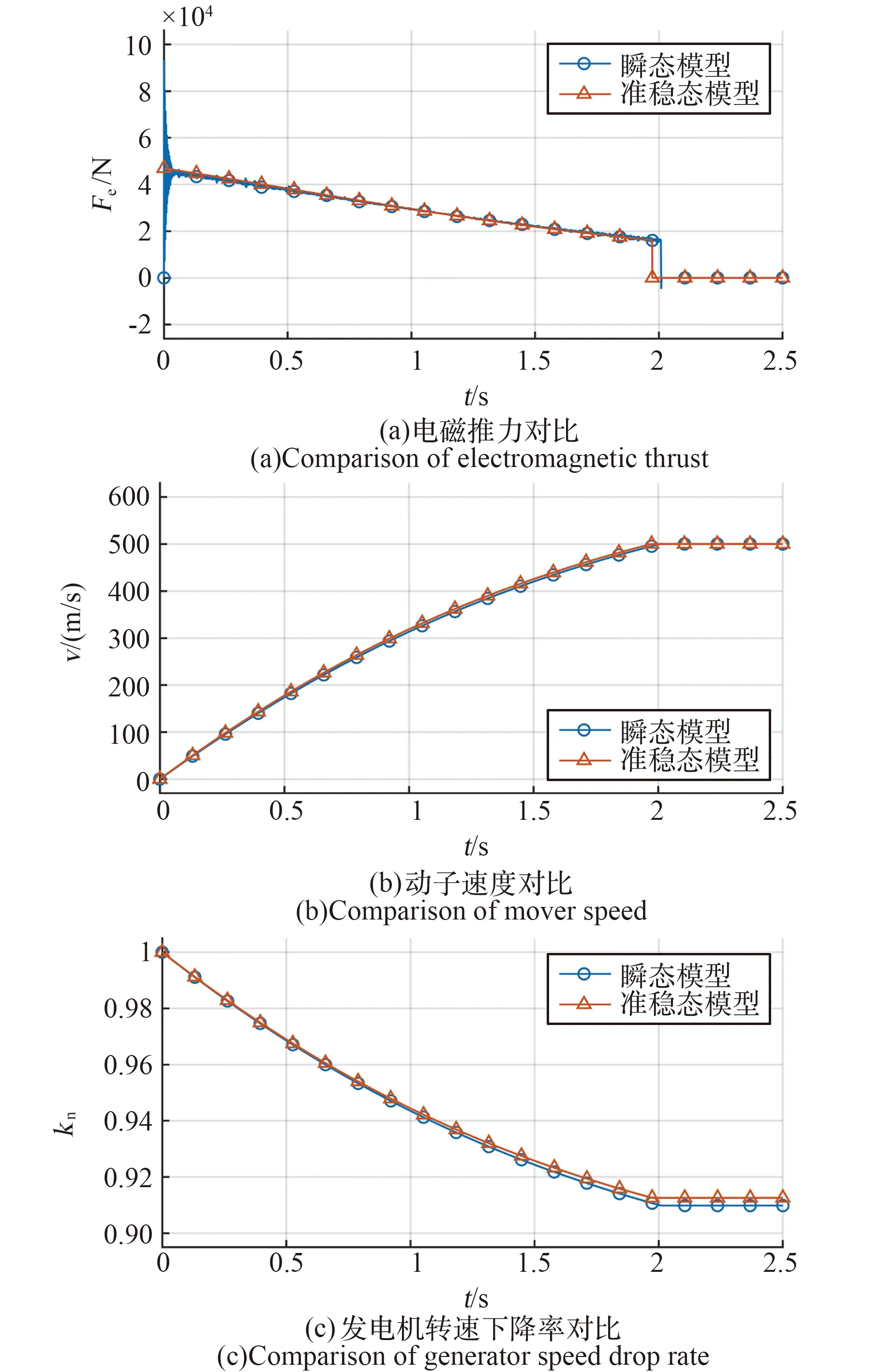
图5 瞬态模型与准稳态模型结果对比Fig.5 Comparison of simulation results between transient model and quasi-steady state model

针对这种时间尺度为秒级的电磁发射过程，通过上述2种模型仿真结果的对比可以发现：采用准稳态模型与采用瞬态模型仿真结果差别并不大；而在仿真速度上，瞬态模型视电机参数不同，其仿真耗时在几分钟到几小时不等，而准稳态模型通常只需几秒钟，远远优于瞬态模型。因此，在需要大量仿真的场合，例如寻找最优电机方案或进行电源参数匹配设计中，采用准稳态模型更加高效和适用。

3 电源参数对发射系统的影响

以表1中的发射系统参数为基础，利用准稳态仿真模型分析脉冲发电机电气参数(电阻、电感等)变化对发射系统性能产生的影响，进而为电源系统方案的优化设计提供依据。

3.1 电阻电感参数

脉冲发电机的电阻电感参数包括定子绕组电阻RsG、定子绕组漏感LlG、直轴电枢反应电感LmdG和交轴电枢反应电感LmqG。设电机分量为式(14)：

(14)

式中：Ladd为交直轴电枢反应电感的平均值，而Lminus为凸极效应对应的电感分量。图6给出了Ladd和RsG参数的变化对发射时间的影响，在Ladd变化时，LlG和Lminus将与Ladd保持原始比例。图中可见，随着Ladd和RsG的减小，发射时长呈缩短趋势，意味着电磁发射性能的提高。

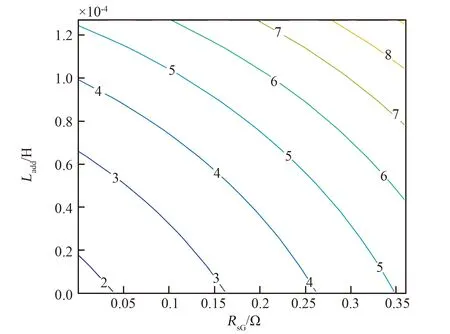
图6 RsG与Ladd对电磁发射时长的影响Fig.6 Effect of RsG and Ladd on time of electromagnetic launch

保持脉冲发电机电阻不变，改变Lminus与Ladd的比例以及LlG与Ladd的比例，分别得到了不同Ladd下，发射时间T随着比值Lminus/Ladd和LlG/Ladd的变化趋势，如图7和图8所示。从图中可以看到，发电机漏感LlG和电感分量Lminus的增大均将导致发射时间延长，而随着电感分量Ladd的增大，这一影响将更加明显。

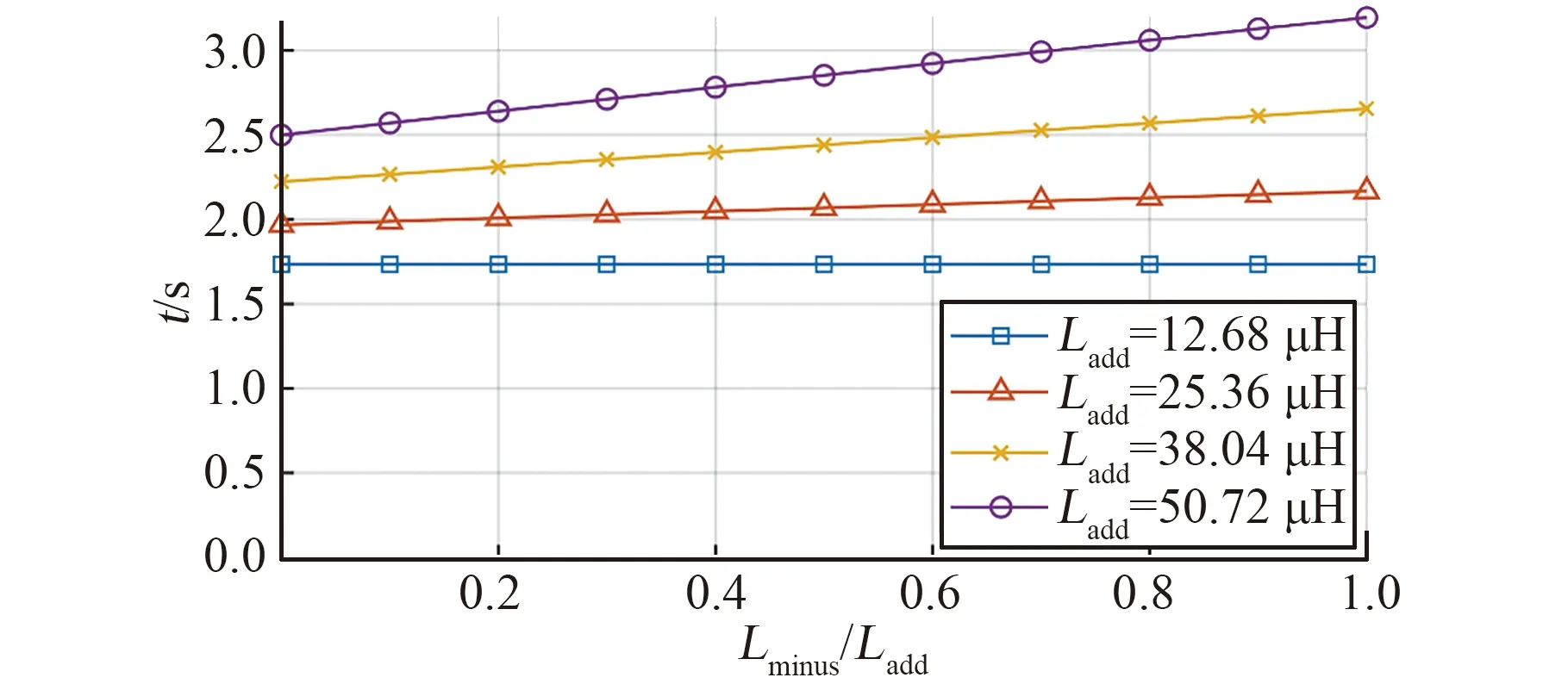
图7 不同Ladd下Lminus/Ladd对发射时长的影响Fig.7 Effect of Lminus/Ladd on launch time under different Ladd

图8 不同Ladd下LlG/Ladd对发射时长的影响Fig.8 Effect of LlG/Ladd on launch time under different Ladd

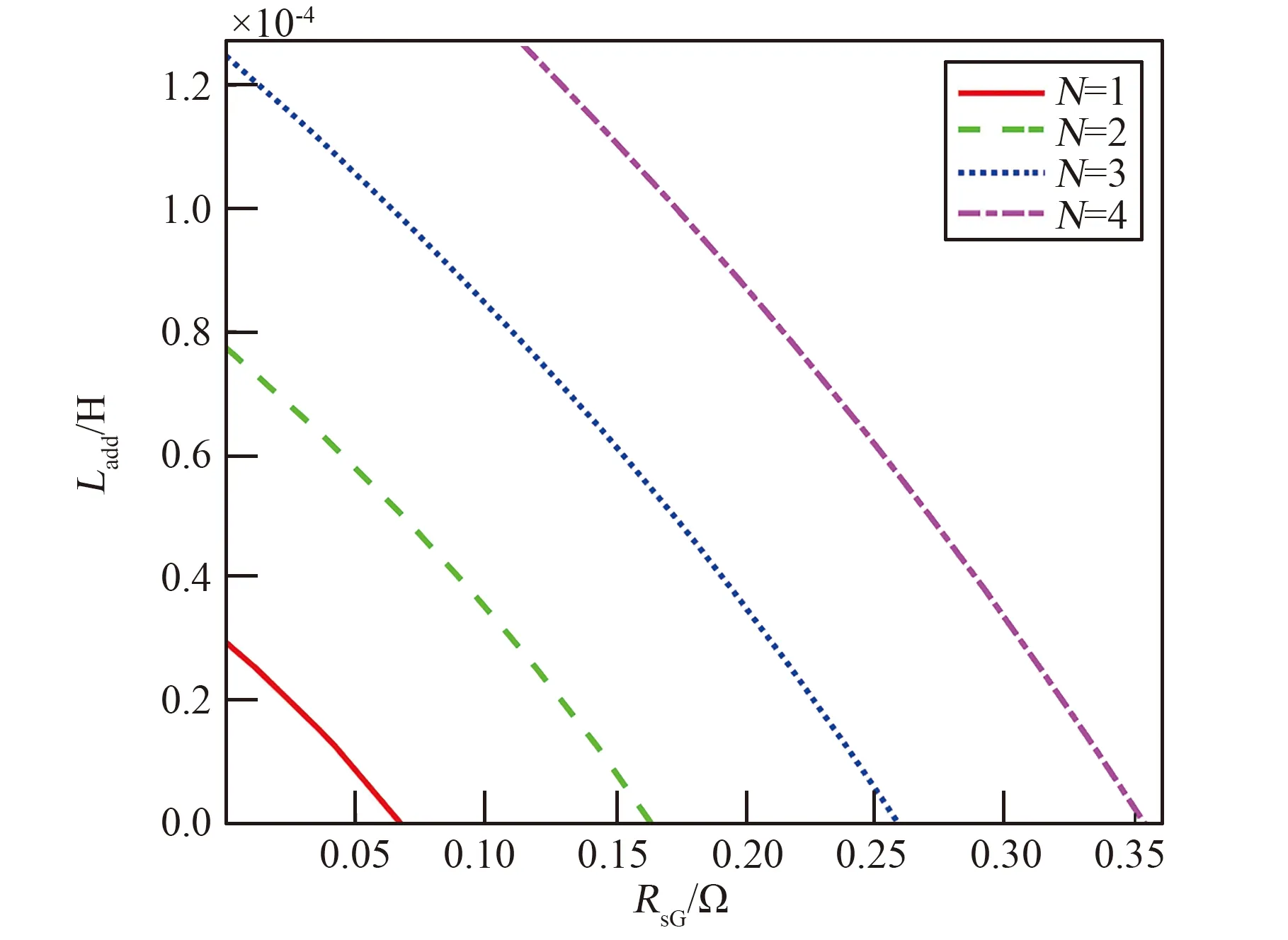
图9 发射时长相同时发电机台数与单机参数的关系Fig.9 Relationship between N and parameters of a single machine under same launch time

3.2 发电机并联台数

电磁发射对电源系统输出功率要求较高，这对发电机参数设计提出了较高要求，从图6中可以看到，单台发电机供电时，要使得发射时长越短，就需要发电机的电阻电感参数设计得越小，电机的体积重量将变得过于庞大，此时可以采用多台发电机并联的方式加以解决。

图9为要求发射时长为2.2 s、采用N台发电机并联时，每台发电机所需的电阻电感参数大小。在改变发电机台数N时，保持发电机的总储能EG不变。从图中可以看到，发电机并联台数越多，每台发电机允许的电阻电感参数就可以取得越大，设计难度和单台电机质量都将随之降低。

4 结论

1) 随着发电机定子电阻RsG和交直轴电枢反应电感平均值Ladd的减小，发射时长将相应减小，电磁发射性能提高；

2) 发电机定子漏感LlG与Ladd的比值以及Lminus与Ladd的比值增大时，发射耗时均会变长，且Ladd越大，这两个比值对发射时长的影响将越大；

3) 发电机并联台数越多，对每台发电机的功率要求越小，单台发电机电阻电感参数可以设计得更大。