宝剑锋从磨砺出
——一道中考数学适应性考试综合题的命制回顾
陈江嵩
(浙江省乐清市乐成第一中学 325600)
随着评价机制改革深入,中考试题的命制也更关注数学思想的渗透及学生数学核心素养的发展,以函数与几何为背景的综合题越来越占据主导.笔者与同行分享参与2018年乐清市中考适应性考试综合题的命制过程中所体现的数学思想与核心素养.
一、试题呈现
如图1,Rt△ABC,CA⊥BC,AC=4,在AB边上取一点D,使AD=BC,作AD的垂直平分线,交AC边于点F,交以AB为直径的⊙O于G,H,设BC=x.

(1)求证:四边形AGDH为菱形;
(2)若EF=y,求y关于x的函数表达式;
(3)连结OF,CG.
①若△AOF为等腰三角形,求⊙O的面积;
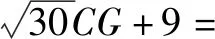
本题属于动态探案型综合题,先通过动点B,带动直角三角形ABC变化,引起直角三角形外接圆的变化,巧妙地将圆与三角形、菱形有机的结合在一起.又通过引入另一动点D,通过AD的中垂线的位置改变,引起菱形AGDH的形变,增加题目的探究性.考生在解题过程中始终要抓住变化中的不变量,对逻辑推理能力有较高的要求.但通过(1)(2)小题的铺垫后,又有利于辅助考生找到这种不变量.总体上,三个问题看似独立,但相互关联,层层深入,逐步递进.
二、命制过程
1.命题立意体现知识与能力并重
本题位于试卷最后一题,双向细目表要求设计一个与“图形与几何”有关的综合性探索问题,其问题的解决涉及初中数学知识的方方面面,要求注重核心知识的覆盖面,立足考查图形基本性质与学生基本能力,包含图形认识、几何计算、合情推理及动态性问题的探索.试题的考查应有层次,要设计一定量适度综合,适度开放,以及有一定探索性的试题,使不同学习程度的学生均有机会发挥自己的真实水平.命题组定出方案:从教材中选取合适素材进行改编,设计动圆与其他图形相结合的动态探究性综合题,用动点带动一组线的变化,动中有静,变中有不变,分层设问,逐步递进,将三角形、四边形、圆、三角函数、方程、轴对称初中数学的核心知识融为一体,要求不同层次学生能够通过阅读理解、推理计算、分类讨论等方式进行一定程度地研究,无论是对知识掌握的要求还是对数学思考能力、逻辑推理能力都要有较高要求,力求体现了“知识与能力并重,思想与方法交融”的特点.
2.素材选取

浙教新版《义务教育教科书·数学》九年级上册第90页例1:如图2,等腰三角形ABC的顶角∠BAC为50°,以腰AB为直径作半圆,交BC于点D,交AC于点E,求弧BD,弧DE和弧AE的度数.
由AB是圆的直径联想到圆周角定理及其推论,尝试连结AD,BE,推得AD⊥BC,问题转化为等腰三角形和直角三角形的性质问题,进而求这些弧的度数,能灵活运用转化思想在提升学生数学运算和逻辑推理能力上至关重要.此例题涉及核心知识面广,设计意图直指数学运算和逻辑推理能力诊断,值得深入研究.命题组确定以此例题为素材通过放宽条件或增加动态元素来编制几何探索问题.
3.成稿过程
(1)由静化动提升推理能力需求
由静化动,动中求定,经历从变化的动态几何图形中探寻等量关系有助于培养学生空间想象能力,进一步考查学生思维严密性,体现分类讨论思想,这是思维层次的飞跃,无疑是逻辑推理能力再提升.以例1为基础,改变设置条件让其中某个直角三角形三边确定,将另一个直角三角形的一个顶点改为在某条直线上的动点,随着动点的运动,相关的直角三角形会发生形变,带动它的外接圆也随之改变,这样此圆与图中某些线段的交点位置也会发生改变,根据这样的命题思路将几何问题与相对应的几何图形进行适当的调整,形成初稿:

如图3,在Rt△AEC中,AC⊥EC,EC=3,AC=4,点B是EC延长线上一点,以AB为直径的⊙O交直线AE于点D,设BC=x.
①用含x的代数式表示AD的长;
②若△ABE是等腰三角形,求AD的长.

(2)添加元素适应思维层次需求
命题组审查后认为初稿虽能体现几何探索题的基本要求,但作为试卷的最后一题的综合题,设问要层层递进,难度成阶梯上升,初稿的第①问还需要降低难度,使学生容易找到切入口.命题组通过讨论确定在第①和第②问前再设计一个切入点低的问题,将原来的①和②改为②和③.完成新加入的第①问设计后,又感觉问题从整体上还存在一些问题:分类讨论思想的考查过多,设问点牵扯线段AD过多显得单一,图形还不够丰富饱满,考查的核心知识有重复,不能够全面考查学生的综合能力,命题组决定做优化处理.
在线段上增加一个动点,并引入垂直元素,让设问点间有联系且丰富多样,增强问题的综合性,考查的思想方法更加多样,其中还将部分线段隐去,几何图形重新做了再调整,形成了第二稿:

如图4,Rt△ABC,CA⊥BC,AC=4,在AB边上取一点D,使AD=BC,作AD的垂直平分线,分别交AC,CB于点F,M,交以AB为直径的⊙O于G,H,设BC=x.
①当x=3时,求EH的长;
②若EF=y,求y关于x的函数关系式;
③连结OF,CG.
(ⅰ)若△AOF为等腰三角形,求⊙O的面积;
(ⅱ)若0 设置AD=BC的条件,确定线段上的动点D受制于点B的运动,由BC (3)增减线段兼顾全面体现数学美 从知识内容上说,第二稿考查的知识内容是丰富了一些,但对于一个综合题而言只有三角形没有四边形问题,总感觉知识的覆盖面不够,从关联性上看,第①问对于第②、第③问缺少关联.于是命题组建议利用圆的轴对称性,连结HA、AG、GD、DH,获得四边形AGDH,可以考虑对四边形AGDH设问,学生可以利用第①题的结论,根据几何图形的特征,寻得线段间的相互关系和等角间相互转换,为第③问作好铺垫.根据以上思路形成第三稿: 如图5,Rt△ABC,CA⊥BC,AC=4,在AB边上取一点D,使AD=BC,作AD的垂直平分线,分别交AC,CB于点F,M,交以AB为直径的⊙O于G,H,设BC=x. ①求证:四边形AGDH为菱形; ②若EF=y,求y关于x的函数关系式; ③连结OF,CG. (ⅰ)若△AOF为等腰三角形,求⊙O的面积; (ⅱ)若0 (4)问题设问指向明确突显本质 基于学生数学素养需求合理设计问题突显教育公平.根据双向细目表初步确定考查的核心知识,还要考虑学生的基本能力和学生数学素养提升,力求知识与能力并重.编制的题目首先要考虑问题的科学性、适标性、有效性和难易性,还要让编制问题应具有解法多样性.成题后作为编题者自己要认真从各个角度思考,探寻方法的多样性,探寻方法还不局限于学生现有知识体系,应该要包括学生后续要学的内容和思想,甚至那些对初中生不作要求的研究方法,如前述第(3)问中求CG的长可以用不同方法构造直角三角形求解,还有可以运用余弦定理或托勒密定理求解.比较各种方法,要充分考虑问题设计不能出现对已学过高中内容或参加过竞赛拓展学习的学生有明显优势,问题设计考虑要基于初中学生的数学思维与数学思想的需求,在试卷的命题设计上体现教育公平.如若出现上述不符合命题初心的问题要考虑改变题目的条件与设问方式,使初中生能够用他们所学的知识解决,着重满足学生需求的思维.
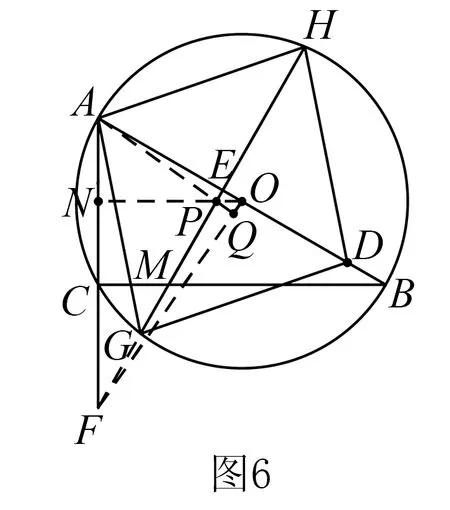


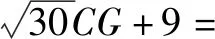
三、体会

