巧解“按比例分配问题”

郭 娟

(山东省泰安肥城市石横镇南大留小学 271612)

按比例分配问题是青岛版小学数学六年级上册第四单元信息窗2的知识点，它是在学习了信息窗1“比”的有关知识基础上安排的学习内容.按比例分配问题是把一个数量按照已知的比分成两部分，是“平均分”题的发展和拓展.

一、学习例题，掌握方法

信息窗2呈现的信息是：明明的体重是30千克，爸爸的体重是70千克.科学研究表明，儿童体内水分与其他物质的比是4∶1；成年人体内水分与其他物质的比是7∶3.课本中提出了两个问题:

问题一：明明体内的水分及其他物质各有多少千克？

问题二：爸爸体内的水分有多少千克？

下面解决问题一：

方法一：要引导学生重点理解“儿童体内水分与其他物质的比是4∶1”的含义.儿童体内水分与其他物质的比是4∶1，就是把明明的体重平均分成5份，水分占其中的4份，其他物质占1份.

总份数：4+1=5，

水分：30÷5×4=24(千克)，

其他物质：30÷5×1=6(千克).

这种方法是根据总份数是5份，用30÷5表示出平均每份的千克数，再乘份数就得出了水分和其他物质的千克数.这是把比看作平均分得的份数，用平均分的方法来解答.

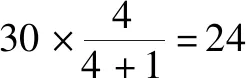
对上面两种做法可以做一些改进：

方法三：4+1=5(求总份数),

30÷5=6(千克) (求1份的千克数),

6×4=24(千克) (求明明体内水分的千克数),

6×1=6(千克)(求明明体内其他物质的千克数),

答：明明体内的水分有24千克，其他物质有6千克.

方法三有四步，每一步都是在整数范围内进行的运算，在计算上很简单.这种方法是把“按比例分配问题”与“整数平均分问题”联系起来了.解题方法变得简单、易懂，易于学生理解和掌握.

方法四：4+1=5(求总份数),

答：明明体内的水分有24千克，其他物质有6千克.

方法四有三步，第一步是整数范围内的计算，第二步和第三步是求一个数的几分之几是多少，运用的知识是分数乘法.这种方法是把按比例分配问题与分数乘法联系起来了.解题思路和方法也容易为学生理解和掌握.

在实际做题过程中，一部分学生喜欢方法三，而另一部分学生喜欢方法四.为什么会出现这两部分同学的不同选择呢？经过调查和研究发现：大部分学生认为方法三更容易理解、更乐于为他们所接受，因为这个方法的所有计算都是在整数范围内思考和解决问题的，学生对这部分知识是熟悉的，思考问题也容易些.方法四是在分数范围内思考问题，一部分学生对这部分知识的运用还达不到运用自如的程度.

仿照问题一的解法，学生自主解答问题二.

二、典型题目练习，注重方法的灵活性

下面是课本46-47页的自主练习中的几个比较典型、 有趣的“按比例分配问题”的题目的解答，解答过程充分体现了方法的灵活性，对学生的思维是一个很好的训练和启发.

第6题：学校修整校园用的混泥土是按2份水泥、3份石子和5份沙子的标准混合成的.现在要用150吨混泥土，需要水泥、石子和沙子各多少吨？

方法一：2+3+5=10,

150÷10=15(吨).

15×2=30(吨),

15×3=45(吨),

15×5=75(吨).

答：需要水泥30吨、石子45吨、沙子75吨.

方法二：2+3+5=10,

答：需要水泥30吨、石子45吨、沙子75吨.

这是一道按比例分配拓展应用的题目，按比例分配的对象由两个量拓展到3个量.按照3个量分配与两个量的解题思路及方法是相同的.

第7题：某市举行小学生唱歌比赛，对进入决赛的选手按2∶3的比评出一、二等奖.如果获二等奖的选手有21名，获一等奖的选手有多少名？

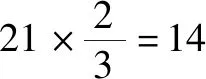
答：获一等奖的选手有14名.

方法二：21÷3=7(名),

7×2=14(名).

答：获一等奖的选手有14名.

第12题：园林公司派出21人为居民区进行绿化.桃园小区的绿化面积是900平方米，绿园小区的绿化面积是700平方米，盛华小区的绿化面积是500平方米.如果按三个小区的绿化面积分配人员，应如何安排人数？

方法一：900+700+500=2100.

答：桃园小区安排9人，绿园小区安排7人，盛华小区安排5人.

方法二：900∶700∶500=9∶7∶5

9+7+5=21

21÷21=1(人)

1×9=9(人)

1×7=7(人)

1×5=5(人)

答：桃园小区安排9人，绿园小区安排7人，盛华小区安排5人.

方法三：900∶700∶500=9∶7 : 5,

9+7+5=21.

答：桃园小区安排9人，绿园小区安排7人，盛华小区安排5人.

第12题的方法二和方法三是化简比(900∶700∶500=9∶7∶5)后，再进行计算，计算过程变得很简单，计算量也很小.这是灵活处理问题的结果.而方法一的计算量是比较大的，做题过程显得啰嗦和复杂.

三、善于总结，提高能力

做题时选择做题方法是非常重要的.要先认真读题、审题，先思考、善于联系所学知识，灵活地选择恰当的方法做题.平时要养成比较做题方法、及时总结做题技巧的习惯，日积月累，数学思维和数学方法会逐步地掌握.学习数学的兴趣逐渐地培养起来，运用所学知识解决实际问题的能力也会逐步得到提高.