对微积分学教育教学中构建学生“数学极限思想”的研究

王智勇 王春秀

摘  要：文章针对努力实现“高职教育培养高素质技能型专门人才”的目标定位， 解读数学极限思想概念和数学极限思想的本质特征，从古人数学极限思想萌芽到青年学生的认知模型和认知特质，探索出高等数学中的基础模块——微积分学的教育教学中构建学生“数学极限思想”的路线图。

关键词：极限思想;本质特征;认知模型;路线图

Abstract： To achieve the object of cultivating many professionals with special skills and abundant competence， this paper firstly analyzes the concept of mathematic limits ant its essence. Next， according to college students' cognition traits， it finds out one route to building the thinking model of mathematic limit in giving a lecture on calculus.

Keywords： concept of mathematic limits; essence; cognition model; route

微积分学作为高等数学之基础，绝不仅仅是解决问题的工具，其中蕴涵着博大的科学思想之一——“数学极限思想”，是数学教育教学不可忽视的，正如日本数学家、数学教育家米山国藏在其专著《数学的精神、思想和方法》中论述到：“无论对于科学工作者、教师人员，还是数学教育工作者，最重要的就是数学的精神、思想和方法，而数学知识只是第二位的。”[1]“如果教师们利用数学教科书，向学生们传授这样的精神、思想和方法，并通过这些精神活动以及数学思想、数学方法的活用，反复地锻炼学生们的思维能力……纵然把数学知识忘记了，但数学精神、思想、方法也会深深铭刻于脑海里，长久地活跃于日常的业务中。”[1]可见，学生将数学知识忘却了以后，剩下的核心成分是数学精神和数学思想方法。然而，现实状况是，在高职高等数学教育教学中，普遍存在重视数学理论教学和数学理论应用教学，而忽视了“深深铭刻于脑海里”的起到重要教育意义的人文思想之一——“数学思想”。这种现状，与“教书育人”的基本原则相悖，与习近平总书记提出的“三全育人”的总体要求不相适应，与高职教育培养高素质技能型专门人才的目标定位相差甚远。挖掘高等数学教育教学中的数学思想，全方位多角度地开展学生思想素质教育，提高高职数学教育教学效能，成为高职院校数学教育工作者必须面对的课题。本文从数学极限思想的本质特征、青年学生的认知模型的视角，探索出高等数学中的基础模块——微积分学的教育教学中构建学生“数学极限思想”的路线图。

一、数学极限思想概念和数学极限思想本质特征的解读

（一）数学极限思想概念的解读

所谓数学极限思想，是指用极限概念、极限性质、极限准则、极限公式和极限运算方法、极限分析方法，进行认识问题、判断问题、逻辑证明问题、严密分析问题和解决问题的一种数学思想。“数学极限思想”构成的理论体系在于：

第一，数列极限概念及数学表达式;

第二，函数极限中的自变量六种变化过程及数学表达式;

第三，函数极限概念及数学表达式;

第四，极限性质和极限准则;

第五，极限运算法则和极限运算方法;

第六，函数极限的两个重要极限公式：

第七，极限的一系列分析方法;

第八，无穷大、无穷小的概念，无穷小的性质，无穷大与无穷小的关系等。

（二）“数学极限思想”的本质特征

数学极限思想不仅贯穿整个微积分学理论，而且在高等数学的微分方程、级数理论、积分变换、概率论与数理统计等，以及建筑工程、机械工程、电子通信、信息工程、自动化控制工程等方面都有广泛的应用。“数学极限思想”揭示了一系列对立统一及矛盾相互转化的辩证规律：

第一、它揭示了无限与有限的对立统一关系。“无限”与“有限”是反映事物发展变化的不同程度，两者既有联系，又有本质的不同。例如，无限个循环小数的和，不是一般的代数和，把它定义为“部分和”的极限，就是借助于极限的思想方法，从“有限”来认识“无限”的，从“已知”世界探寻“未知”世界。例如：

第二，揭示了常量与变量的对立统一的关系。按照辩证唯物主义观点，“变”是绝对的，经常的，永恒的，而“不变”是相对的。“变”与“不变”反映了事物变化发展与事物相对静止的两种不同状态，但它们在一定条件下又可以相互转化，这种转化是“数学极限思想的有力杠杆之一”。例如，要求变速直线运动质点在某一时刻的瞬时速度，用初等方法是无法解决的，困难在于速度是变量。为此，人们观察到很小很小的时间段内，速度改变也很小很小，把小时间段内的变速运动，看成匀速运动，用匀速代替变速，并求其平均速度，再把瞬时速度定义为运动时间段无限短的平均速度的极限。

第三，揭示了直线与曲线的对立统一的关系。“曲线”与“直线”有着本质的差异，但在一定条件下也可相互转化，在生活中的木桶由等长的小矩形木板镶成的，小矩形木板的宽为短直线段，而木桶的上下底面圆周为圆周弧线，在这里，“直线形”与“曲线形”实现了转换。恩格斯在《自然辩证法》一束中感叹道：“直线和曲线在微分中终于等同起来了。”[2]善于利用这种对立统一关系是处理数学问题的重要手段之一，例如直线形的面积容易求得，求曲线形的面积问题用初等数学方法是不能解决的。

第四，揭示了量变和质变的辩证规律。量变的積累，到达一定的程度能引起质变，质和量的互变规律是辩证法的基本规律之一。例如，生活中的蔬菜茄子，不是一个规则的圆柱体。当我们将茄子平放在菜板的平面上，用垂直于菜板的平面，不停地截茄子，任取其中的薄片茄子，仔细观察，这一薄片茄子几乎变成了一个薄薄的圆柱体。再把茄子截得越薄，则薄片茄子就无限接近一个规则的薄圆柱体，而规则的圆柱体的体积有公式计算，计算得来的体积，是一个近似值，进而将每个薄片茄子的体积（近似值）进行无限叠加（求和）后，再取极限（积分），就能计算出茄子的体积。这种“分割——取近视——求和——取极限”的过程中，就是数学极限思想的直接应用。

第五，揭示了近似与精确的对立统一关系，两者在一定条件下也可相互转化，这种转化是高等数学应用于实际计算的重要诀窍。例如，微分的近似由变量比计算公式：

二、古代极限思想的萌芽与青年大学生的认知特质解读

（一）古代极限思想的萌芽

在生产力落后的古代，我们的祖先对有限、无限问题认识不断深化，逐渐形成数学极限思想的萌芽。公元前三世纪战国时期出现的《庄子·天下篇》中有：“一尺之棰，日取其半，万世不竭”的名言，萌芽出了无限细分的极限思想;到了公元三世紀，我国三国时期的数学家刘辉，将庄子的无限细分的极限思想，用在了圆的面积的计算，他在《九章算术》中采用了正多边形对圆周不断分割，得出“割之弥细，所失弥少，割之又割，以至于不可割，则与圆合体，而无所失”的无限逼近的数学极限思想方法。

（二）高职大学生的认知模型和认知特质的解读

从认知的总体视角看，认知发展是从初级向高级，从简单到复杂方向发展的。青年大学生历经小学到中学系统的连续的学习和接受教育，认知得到极大的发展，其认知过程和认知能力，都是多层次的，多结构的。具体体现在：

（1）青年大学生们注意力的集中性和稳定性，得到了很好的发展，注意力达到成年人的水平;

（2）青年学生们记忆的自觉性和目的性，得到很大的提高，能坚持运用有意义的识记方法;

（3）青年学生们的理解能力也有很好的发展，对学习内容，能寻找内在联系，抓住主题，分清重点;

（4）青年学生们的抽象思维能力在不断发展，经历了感知行动思维、具体抽象思维和抽象逻辑思维等阶段。

（5）尽管青年学生们的这些认知能力具有个体差异性和观察的不确定性，但是，学生们的认知水平都会遵循认知数学模型：

三、微积分学的教育教学中，构建高职学生“数学极限思想”的路线图

（一）在微积分学的教学内容中挖掘“数学极限思想”

对学生而言，数学问题（案例）提出和思考的过程，数学概念的理解和建立过程，数学方法（性质或规则）的形成和运用过程，数学原理（定理）的理解和证明过程，数学规律的熟悉和掌握过程等，都是高职学生数学思想感觉、发现、提出、渗透、理解、提炼、归纳和逐步建立的过程，也是学生数学思想归纳、总结和深化的好时机，更是数学老师挖掘数学教学内容中的数学思想，对蕴含在不同数学教学内容中看似“碎片化”分散的数学思想，进行条理化和系统化整合的好路径。例如极限理论知识教学中的数列极限概念及数学表达式、函数极限中的自变量六种变化过程及数学表达式、函数极限概念及数学表达式、极限性质和极限准则、极限运算方法，函数极限的两个重要极限公式，以及极限的一系列分析方法等极限知识，不仅仅是构成极限理论知识和极限分析方法，而且蕴含了丰富的数学极限思想，有待数学教师在数学极限教育教学中挖掘出“数学极限思想”，有意识有目的进行数学极限思想教学;又如以数学极限理论知识为基础，主要研究变量变化的速度和大小问题，建立导数和微分概念及微分学理论，是研究函数性态的有力工具，用微分学分析函数变化形态的过程中，离不开分析讨论“常量与变量”、“连续与间断”、“直与曲”、“凸与凹”、“极大与极小”、“最大与最小”等，用“数学极限思想”揭示的一系列对立统一的辩证规律。微分学的建立和微分学中蕴含的数学极限思想不仅对数学的发展产生了深远的影响，而且渗透到自然科学、工程技术、社会经济等各个领域。结合微分学应用的典型例题分析与讲解，带领学生在“用数学”解决实际问题中揭示“数学极限思想”，反过来又用“数学极限思想”分析解决实际问题。

数学极限理论知识、数学极限思想和数学极限方法三者，相互交织，融为一体，需要数学老师在数学教材中认真挖掘数学极限思想，有意识的深化“数学极限思想”的渗透;从极限理论知识、极限方法和极限思想的逻辑角度分析与把握，熟悉教材的知识体系与知识要点的脉络、地位与作用、重点与难点，还要按照极限实例（案例）、极限概念的建立、极限理论知识的理解、极限计算等知识板块的教学结构中，挖掘、寻找和总结“数学极限思想”;从数学极限的教学中提炼和概括极限思想，又把提炼和概括的极限思想反馈到极限理论知识的进一步理解、掌握和应用中，一步一步地积累学生的极限理论知识和形成学生自觉行动的数学极限思想，进而形成学生全面的极限理论知识和极限思想体系。

（二）在数列极限和函数极限的一系列概念形成的过程中渗透“极限思想”

数学极限概念的教学，是建立在已有的基础知识和熟悉的典型事例的前提下，与学习理解新知识之间建立起内在联系，包括数学极限问题的提出→极限概念初步形成→极限概念的建立→极限概念的概括和极限符号的准确表达等内容。教学中用几何图形的直观表达，让学生更容易理解抽象的极限概念及其表达式、极限性质和极限准则等，形成数学极限思想的初步印象;用典型的数学极限例题分析，帮助学生在用极限概念、极限性质、极限公式和极限运算方法解决问题的过程中，加深极限概念的理解，熟悉极限公式和极限运算方法的应用，逐步建立数学极限思想。

数学极限概念包括数列极限、自变量无限增大时函数的极限、自变量无限趋近于某一点时函数的极限、自变量无限趋近于某一点时函数的单侧极限（即左极限和右极限）。人类对数学极限的认识，不是一蹴而就的，经历了数学极限认识的萌芽→极限深入思考的困惑→极限概念的深刻认识与表达的过程。数学家对数学极限的认识和定义，进行了艰苦的探寻过程，直到19世纪，德国数学家威尔斯特拉斯提出严格化静态化的极限定义，即为“ε-Ν”函数f（x）在x→∞时的静态化极限定义：

数学家威尔斯特拉斯“ε-Ν”静态化极限定义的成功，在于消除了历史上关于极限各种模糊的表述，诸如“最终比”、“无限趋近于”、“无限接近于”等等，消除了历史上形成的多年的“贝克莱悖论”。数学家威尔斯特拉斯极限定义中发明的“ε-Ν”数学语言表达方式的奥妙在于，正数ε>0（不论它多么小）是任意给定的，蕴含了辩证的逻辑思想：

其一，正数ε具有确定性，一旦给定，就不能变了;

其二，正数ε具有任意性，在选定之前，具有变化的特性，可以看成变量;

其三，只要给定正数ε，总存在正数y>b。即是说正数ε与正数y之间建立了某种对应关系，即函数关系。

这一严谨科学的极限定义，清晰地表达了函数极限中蕴含的“流动性，不确定性和无限性”思想和过程逻辑确定性思想;这一严谨科学的极限定义，具有数学语言独特表达的抽象性，学生理解这一函数极限的定义有困难，教师在教学过程中，用生活中或发生过较容易理解的直观的案例，多角度全方位的分析讲解，引导学生理解和建立极限概念中的“流动性，不确定性和无限性”思想和过程逻辑确定性思想。

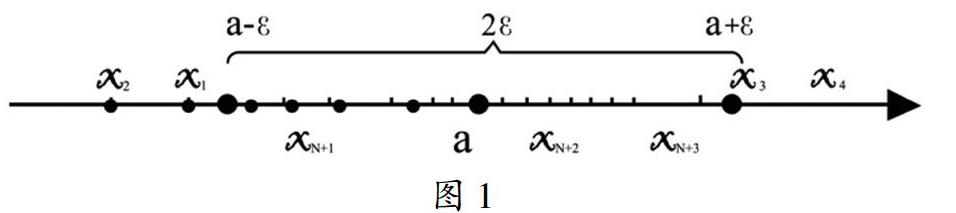
数列{xn}收敛于a的几何意义：

1. 将数列{xn}中的项，放置于数轴上时，数列{xn}收敛于a就意味着对于无论多么小的正数ε，对于区间（a-ε，a+ε）（即为点a的领域 U（a+ε）），总存在正整数N，使得数列{xn}的点列x1，x2，x3，x4......xn......的第n个点xN，以后所有的点xN+1，xN+2，xN+3，......都落入邻域 U（a+ε）内。

2. 如图1所示

3. 数列{xn}极限定义中的正数ε，是任意给定的，正整数N是随着正数ε的给定而确定的。

通过对数列极限的“代数分析”、“ε-Ν”极限定义分析、理解“ε-Ν”数列极限定义、数列{xn}收敛于a 的几何意义分析，让学生多角度全方位理解数列极限概念，多重理解数列极限和数列极限概念，不仅仅起到深入理解数列极限概念，而且加深了数列极限方法的掌握，建立了数学极限思想。

（三）在数学极限问题解决过程中深入揭示 “数学极限思想方法”

单纯的教授数学方法，无论是在解答数学题，还是解决实际问题，学生很难做到熟练掌握，多数学生在很长时间段都停留在简单的模仿阶段，学到的数学方法也是一些“套路式”的方法。这些“套路式”的方法，缺乏活的“灵魂”或活的“思想”，难以举一反三，灵活运用。

数学的特点之一，就是具有广泛的应用性。学习数学的目的在于用好数学，在于用数学理论思考实际问题和解决实际问题，也就是数学老师引导学生学习数学理论的过程，一个应用数学理论探索实际问题与解决实际问题的过程，在这一过程中，有意识的有目的地深入揭示数学思想，有意识的有目的地总结出数学方法，将“数学思想”与“数学方法”有机结合，形成带有规律性的科学的数学思想方法。数学思想方法一经形成，必然遵循数学原理和数学理论，完全可以指导实践，完全可以反复用之于实践，师生在思考、分析、探索和解决实际问题的过程中，反复运用科学的数学思想方法，不仅能提升他们解决实际问题的能力，而且还能够深化高职学生的数学思想，对高职学生初步形成的数学思想进行整体化和系统化的作用，熟练师生解决问题的数学思想方法，解决实际问题的方法也就变得更有“灵魂”了。

（四）在不同阶段的数学知识学习整理中，归纳、概括、总结和深化“数学极限思想”

数学极限思想的教学必须以数学极限知识和数学极限理论为载体，而数学极限思想又常常分布在许多不同的知识点中，在形式上看，数学极限思想体现出了一定的“分散”的特点。这种“分散”，不是简单的分散，有的分散在数学概念的形成中，如“导数概念的形成”、“无穷小”、“无穷大”、“函数连续”、“定积分概念的形成”等;有的分散在数学问题的解决中，如“曲线上一点处切线的斜率”、 “曲线的曲率”、 “曲边梯形面积”、“变速直线运动的路程”等;有的分散在数学问题的分析认识中，如“曲线连续与间断分析”、“曲线性态分析”等;有的分散在数学新理论理解掌握中，如“级数理论”、“积分变换”、“中心极限定理”等。不同的数学知识和理论中蕴含“数学极限思想”方式不同，不同的数学知识和理论中“数学极限思想”的表达形式也不同，不同的数学知识和理论中“数学极限思想”的思维方式更不同。这种“数学极限思想”在数学知识结构中“分散”和表现方式“多样”的特点，符合“高职大学生的认知特征”，有助于高职学生全方位多角度感悟、认知、理解和掌握数学极限思想;再从辩证法的视角看待，“数学极限思想”在数学知识结构中的“分散”，不是简单的分开，而是体现在一系列数学概念中、一系列数学理论的结构中和一系列数学理论的应用中，数学课程教学中，既要认真挖掘不同数学知识结构中数学极限思想，又要及时地归纳、概括、总结、提炼和深化数学极限思想，将表现方式的“多样化”特点的数学极限思想条理化、系统化、层次化和整体化，引导学生有层次地全面地理解数学极限理论知识和数学极限思想，更系统地和整体地思考数学极限概念的产生、极限的性质、极限形成的知识结构、有关极限新知识的展开……，怎样证明？实质是什么？怎样应用？等等，构建极限理论、极限思想及其应用的良好的认知结构。

五、结束语

数学极限思想方法蕴含了数学极限思想和数学极限方法，更是数学极限思想与数学极限方法的辩证统一。就现有的数学教材中，都没有明确提出或单独提出数学极限思想方法，而是将数学思想和数学方法融入数学教学内容中，渗透到教学的各个环节。教师在教学备课中不仅要钻研数学教材，博览数学文献，而且还要将数学内容中的数学思想和数学方法揭示和挖掘出来，选择好典型教学案例，结合学生实际，把数学极限思想方法列为具体的教学目的，把数学极限思想方法作为实现“教书育人”的重要内容，开展教育教学。在课程教学中，教师应重视数学思想方法的发现、提出、渗透、提炼、归纳、概括、总结、激活、深化和运用。“只有这样，才能引导学生抓住数学思想的精髓，学到真正的知识，培养良好的数学思维能力。”[4]

参考文献：

[1][日]米山國藏.数学的精神、思想和方法[M].四川教育出版社，1986：87-95.

[2]弗里德里希·冯·恩格斯.自然辩证法[M].学习出版社，1998：45-46.

[3]李心灿.高等数学[M].高等教育出版社，2008：55-56.

[4]曹一鸣.数学教学论[M].高等教育出版社，2008：280-232.