哲学思维：超越数学基本思想的思维认知

【摘 要】数学基本思想体现为三大核心要素，即抽象、推理和模型，数学思想中蕴含着丰富的哲学思维。在数学教学中，教师有意识地引导学生从哲学的角度辩证剖析教学内容，将有助于培养学生的哲学思维，使他们从更高的角度认识数学。

【关键词】哲学思维;数学基本思想;抽象;推理;模型

【中图分类号】G623.5【文献标志码】A【文章编号】1005-6009（2020）25-0027-05

【作者简介】李静，南京市北京东路小学（南京，210008）教师，一级教师，南京市优秀青年教师。

《义务教育数学课程标准（2011年版）》把数学教学中的“双基”发展为“四基”，在基本知识和基本技能的基础上增加了基本思想与基本活动经验。数学基本思想是指数学产生与发展所依赖的思想，是人学习数学以后具有的思维能力。数学学科层面之上的思想应该超越数学，上升到哲学的高度。教师在数学教学中有意识地培养学生的哲学思维能力，将有助于学生从更高的角度认识数学。那么，什么是哲学思维？数学基本思想中能挖掘出哪些哲学思维？该如何实现数学基本思想到哲学思维的超越呢？本文将结合具体的教学实践进行初步的阐述。

一、解读：数学与哲学的关联

数学是从数量、结构、变化、空间和信息等角度探究世界规律的学问。哲学是从思辨角度研究世界观和方法论的学问。数学和哲学有着天然的联系。正如数学家B.德莫林斯说的：“没有数学，我们无法看透哲学的深度;没有哲学，人们也无法看透数学的深度。”数学中蕴含着诸多哲学思想，如现象和本质、一和多、部分和整体、永恒和变化等，它们影响着数学的发展。在哲学思维的指导下研究数学，有助于人们认识和理解数学的本质。用哲学思维指导的数学教学，不只在知识内部就事论事，往往还能从数学思想的高度找出解决问题的方法。

二、审视：数学基本思想中的哲学思维

东北师范大学史宁中教授认为，我们可以把数学基本思想归结为三个核心要素，即抽象、推理和模型，三者之间先后关联、起承转合、相互交织。数学思想或隐性或显性地存在于数学教学中，除了能从数学的角度传授知识和方法，还能从哲学的角度进行适度的辩证剖析。

1.抽象思想中的哲学——“日取其半，万世不竭”。

抽象是指从众多对象中抽取出共同且本质的特征，舍弃其非本质特征，它是数学活动中最基本的思想，包括分类、集合、变与不变、符号、对应、有限与无限等。其中，极限思想是用无限逼近的方式来刻画数量变化的趋势，这里要抓住两个关键点：其一是变化的量是无穷多个;其二是无限变化的量趋于一个确定的常数。传统的小学数学计算是有限个数的计算，经过有限的运算次数可以得到一个确定的结果。计算常见几何图形的面积，可以通过分割、平移把它们转化成长方形来推导面积计算公式。但对于不能直接转化成长方形的圆、椭圆等图形来说，又该如何精确计算它们的周长和面积呢？其实，圆也可以分割转化成长方形，只不过一般直边图形是通过有限次分割来转化成长方形的，而圆是通过无限次分割、拼接、逼近来转化成长方形的。这样操作的依据便是极限思想，因而极限思想在小学数学教材及教学中不但有，而且在计算和公式推导中已经真正应用了，是小学数学教材和课堂教学中客观存在的数学思想。

数学的极限思想只是科学的一小部分，往深层次挖掘，就可以看到哲学的成分。《庄子·天下篇》有云：“一尺之棰，日取其半，万世不竭。”这句话转化为数学语言来描述就是：长度为单位1的线段，第一天取走全长的一半，以后每天取走剩下的一半，永远有剩余。其实，这句话只说对了一半。根据极限思想，这个无限变化的结果最后一定有极限，这句话只看到了无限，而没有看到无限中蕴含着有限，无限取下去，剩下线段的长度趋于0，取走的长度趋于1。为了计算圆的面积和圆周率，我国古代数学家刘徽创立了割圆术，先做圆的内接正六边形，再做圆的内接正十二边形，随着正多边形越来越接近圆，它的面积和周长也越来越接近圆的面积和周长。刘徽在描述这种做法时说：“割之弥细，所失弥少，割之又割，以至不可割，则与圆周合体而无所失矣。”也就是说，随着正多边形的边数无限增加，圆就可以转化为边数无限的圆内接正多边形，即化圆为方。刘徽看到了有限与无限的对立统一，比庄子的认识更全面、更客观。由上可知，极限思想是一种用无限逼近的方式来研究数量变化趋势的哲学思维，同时也是微积分理论的基础，本质上体现了辩证关系，即圆与方、曲与直、静与动、有限与无限对立统一的哲学思维。

2.推理思想中的哲学——“塞翁失马，焉知非福”。

推理是從一个命题判断到另一个命题判断的思维过程，包括归纳、演绎、数形结合、转化、类比等。以其中典型的转化思想为例，数学学习中有数的转化、计算的转化、图形的转化等问题，当学生束手无策时，教师若能引导他们运用未知化已知、复杂化简单、一般化特殊、抽象化具体等转化思想来解决，将有助于学生拨开思维的迷雾。在数学教学中，众多现实引发笔者思考：转化思想是引导数学学习和工作的灵魂，如果我们站位更高、眼光更远，能否将转化的思想和意识渗透至我们的生活中呢？

答案是肯定的。我国有句成语叫“塞翁失马，焉知非福”，是说塞翁丢了马，人们都来慰问他，他说：“这怎么就不能是一件好事呢？”几天后马不仅回来了，还带回了许多匹塞外良马，人们都来祝贺他，他说：“这怎么就不能是一件坏事呢？”又过了几天，塞翁的儿子从马上摔下腿断了，人们都来安慰他，他说：“这怎么就不能是一件好事呢？”之后国家征兵打仗，塞翁的儿子因为腿瘸而免于征战。这是一个循环往复、极具戏剧性的故事，阐述了祸与福的对立统一关系，揭示了“祸兮福之所倚，福兮祸之所伏”的道理。如果单从哲学的角度来看，这个成语启发人们用转化的思维、发展的眼光辩证地去看问题。无论是遇到福还是遇到祸，都要辩证地看待未知的结果。

当然，生活中还有很多蕴含着哲学思维的转化思想，如形容情绪大起大落的“乐极生悲”、说明忧患意识重要性的“人无远虑，必有近忧”等成语或俗语。如果教师能在数学教学中加以渗透，学生运用辩证思维看待、分析问题的心态将会更加成熟、平和，这对于现实教学和学生将来的发展都具有实际意义。

3.模型思想中的哲学——“愚者千虑，必有一得”。

数学模型是为解决现实生活中的问题而建立的概念、公式、定义、定理、法则、体系等，一般用语言、符号、数量关系或图形来呈现。模型思想包括简化、量化、函数、方程、优化、随机、统计等。以简化思想为例，它强调将复杂的问题用简单的符号或图示模型来进行表征。如著名的哥尼斯堡七桥问题：一个步行者怎样才能不重复、不遗漏地一次走完七座桥，最后回到出发点呢？瑞士数学家欧拉把它简化成了一个几何问题的模型——一笔画问题，不仅解决了问题，给出了连通图，还提出一笔画的重要条件在于它们是连通的，而且奇顶点（通过此点弧的条数是奇数）的个数为0或2。

有人可能会说，这是大数学家才能想到的方法，我们这些平凡人是难以解决这些高深的问题的。我国西漢史学家司马迁在《史记·淮阴侯列传》中写道：“智者千虑，必有一失;愚者千虑，必有一得。”这是说智者在多次的考虑中也会出现个别错误;而愚者经过千百次的思考，偶尔想出一条主意也可能是正确的。这些所谓的愚者实际上是在践行简化的思想，他们在用最简单的方法下“笨”功夫，这种“笨”功夫实则就是按照一定的模型，循环往复地进行模型化尝试和体验，很好地印证了“实践出真知”的哲学道理。

三、实践：儿童哲学思维的培养对策

1.化隐为显，明晰哲学思维的关键点。

小学生往往对具体的、数量有限的事物比较容易理解，而对抽象的、数量无限的事物难以把握。在数学教学中，教师可以针对他们思维认知的关键点，将隐性的抽象转变为显性的直观，并适度渗透相应的哲学思维。前面提到的“一尺之棰，日取其半，万世不竭”，不妨借助如图1所示的直观图来理解。进一步来看，可以把日取的总和转化为无限个数相加的计算，即 + + + + + +……。还可以用数形结合（如图2）的方法来帮助学生理解。当天数为n时， + + + + + ……+ =1- 。当n无限大时， 就越来越小，木棒剩下部分的长度会趋于0，那么最终的计算结果1- 会越来越接近于1，直至等于1。

解题过程中蕴含着复杂的极限思想。此时，若教师适时点拨，将微观放大，引导学生找到其中哲学思维的生长点，即量变引起质变，其和无限逼近1，将有助于学生加深对极限思想的认识。

2.化弊为利，找准哲学思维的切入点。

在数学教学中，我们不仅应关注知识的传承，还要发现儿童的“独特之处”。首先是“容”错，更重要的是“荣”错，学生的错误是一种宝贵的教学资源，这其实与之前提到的“塞翁失马，焉知非福”的哲学思维不谋而合。下面，我们来看特级教师周卫东执教苏教版五上《平行四边形的面积》一课的两个片段：

【片段1】

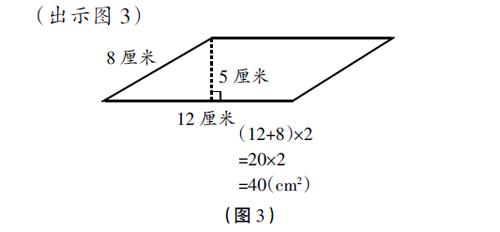
师：同学们课前都自己尝试求了这个平行四边形的面积，我们先来看看这位同学的想法。（出示图3）

师：你觉得他的想法对吗？

生：不对。因为他算的不是面积而是周长。

师：这个想法虽然不正确，但它的价值在哪里？

生：提醒我们要看清楚求的是面积还是周长。

周老师用艺术化的处理告诉大家这样一个哲学道理：学生的错误都有它的价值，都有它存在的意义。

【片段2】

师：刚刚，我们通过切割和平移把平行四边形转化成了长方形，得出平行四边形面积=底×高。有同学课前是这样想的（出示图4），他的想法对吗？（大多数学生摇头）错在哪里了？

生：把这个平行四边形转化成长方形，转化后的长方形的宽是5而不是8，也就是说高是5，所以不能用12×8。

师：你觉得12×8算出来的面积比实际面积大还是小？

生：我觉得这样算应该比实际面积大。

师：能说明理由吗？

学生画出相应的图，教师课件（如图5）演示说明。

师：在这样的变化过程中，面积为什么会变大呢？

生：因为角度在逐渐变大。

师（出示图6）：对，a和b两条边之间的夹角越大，这两条边相乘得出的面积就越大……

周老师把学生的错误转化成了一种有效的教学资源。从学生的错误出发，找准知识结构之间的关联，潜移默化地渗透初中相关知识的学习，让学生真正经历体验、探索、再发现的过程。

3.化繁为简，把握哲学思维的延伸点。

从数学思维的角度来看，问题解决实际上是以问题为载体，引导学生经历抽象和概括的过程。笔者前面谈到了模型思想，简言之，数学模型就是借助数学的语言讲述现实生活的故事。特级教师华应龙“投石问路”的教学方法就是一个很好的例证。

课始，华老师出示微信朋友圈中的一个话题——“徒弟问：‘师父，您多大了？师父答：‘我在你这年纪时，你才5岁;等你到我这年纪时，我就71岁了。”并提问：徒弟几岁？师父几岁？问题一出来，大部分学生面面相觑。华老师让学生多读几遍，提炼出几个关键词：过去、现在、将来，并画出如图7所示的示意图。进而提出如图8所示的“投石问路”画图法，让学生也像这样举例并画图表示。

师：投石是为了什么？

生：问路，找到问题之间的关系。

师：真好，你发现什么关系了吗？

生：通过投石问路，能看出从徒弟过去的5岁到师父将来的71岁，中间共相差66岁，里面有3段年龄差，每一段年龄差就是22岁。

…………

华老师这节课旨在引导学生建构相应的数学模型，搭建帮助理解的思维脚手架，题目中的实质性知识并不重要，他要以此聚焦、凸显比“鱼”更重要的“渔”，而且这“渔”并非由他所传授，他只是在“导人自渔”。“投石问路”的方法看似愚笨，实则是一种简化的理性思维训练。“愚者千虑，必有一得”，就在这笨与不笨的冲突中，学生向下“沉潜”，在试错与摸索中触及知识内蕴，进而“向上飞扬”，沉潜似“笨”，飞扬为“智”。

数学教学的最终目标，是让学生会用数学的眼光观察现实世界，用数学的思维思考现实世界，用数学的语言表达现实世界。而数学的眼光就是抽象，数学的思维就是推理，数学的语言就是模型。学生通过数学学习掌握数学思想方法，学会思考和判断，可以更容易地理解哲学的基本原理，形成哲学思维。教师应不断提升自己的哲学素养，用数学基本思想背后的哲学思维来指导教学，这样不仅有助于学生潜移默化地掌握哲学的思维方法，也能使他们从更高的角度认识数学、理解数学，进而提高思维能力、推理能力和创新能力。

【参考文献】

[1]徐长林.《塞翁失马》中的消极思想[J].语文教学通讯：初中（B），2011（2）：50.

[2]王永春.小学数学思想方法解读及教学案例[M].上海：华东师范大学出版社，2017.

[3]于漪.教海泛舟，学做人师[J].人民教育，2010（17）：53-59.

[4]段安阳.数学思想的内涵、价值及教学建议[J].江苏教育：小学教学，2013（10）：33-35.

[5]曹琴珍.中小学数学学科渗透儿童哲学教育的意义与方法探析——以“人教版七年级上册数学几何图形初步”为例[J].福建教育学院学报，2019（1）：34-37.

[6]陈晓兵.数学与哲学之间的紧密联系[J].青少年日记：教育教学研究，2013（10）：96.

注：本文获2019年江苏省“教海探航”征文竞赛一等奖，有删改。