定义在多重互素GCD封闭集上Smith矩阵行列式的整除性

胡双年，李艳艳，朱玉清，牛玉俊

（1.南阳理工学院数学与统计学院，河南南阳473004； 2.南阳理工学院电子与电气工程学院，河南南阳473004）

设f为算术函数，S＝｛x1，x2，…，xn｝是由n个不同的正整数构成的集合.用（f（S））＝（f（xi，xj））（1≤i，j≤n）表示一个n阶方阵，其i行j列处的元素为f在xi和xj的最大公因子（xi，xj）处的取值.用（f［S］）＝（f［xi，xj］）（1≤i，j≤n）表示另一个n阶方阵，其i行j列处的元素为f在xi和xj的最小公倍数［xi，xj］处的取值.设a为正整数.若对任意给定的正整数x，算术函数f定义为f（x）＝xa，则（f（S））＝（Sa）和（f［S］）＝［Sa］分别称为a次幂最大公约数GCD（greatest common divisor）矩阵和a次幂最小公倍数LCM（least common multiple）矩阵.当a＝1时，简称（S）为定义在S上的GCD矩阵，［S］为定义在S上的LCM矩阵.对于任意的正整数x∈S，如果x的任意正因子d∈S，则称S为因子封闭集.1875年，Smith［1］率先研究了定义在集合S＝｛1，2，…，n｝上的GCD矩阵的行列式，他证明了如下结果成立：定义在集合S＝｛1，2，…，n｝上的n阶GCD矩阵（S）的行列式，其中φ是欧拉函数.同时也得到了定义在因子封闭集S上的n阶GCD矩阵（S）的行列式和n阶LCM矩阵［S］的行列式

其中对于任意的素数p和正整数r，乘法函数π定义为π（pr）＝-p，并且Smith［1］也证明了定义在因子封闭集S上的n阶矩阵（f（S））的行列式为

其中，μ为Möbius函数，f*μ是f和μ的Dirichlet卷积.1989年，Beslin等［2］推广了Smith的结论，给出了定义在最大公因子封闭集S（对任意的x，y∈S，（x，y）∈S）上的行列式

1992年，Bourque等［3］证明了当S为最大公因子封闭集时，

其中g为乘法函数，定义为

从此，人们称定义在整数集合上的矩阵为Smith矩阵.关于Smith矩阵的研究在近几十年特别活跃，参见文献［2-14］.在Smith矩阵的研究领域中，整除性问题是中心研究课题之一.设S是因子封闭集，Bourque等［3］证明了在整数矩阵环Mn（Z）中，GCD矩阵（S）整除LCM矩阵［S］（即存在n阶的整数矩阵A，使得［S］＝A（S）或［S］＝（S）A）.2002年，Hong［8］证明了对任意GCD封闭集S，如果｜S｜≤3，则在整数矩阵环Mn（Z）中，GCD矩阵（S）整除LCM矩阵［S］，对于｜S｜＞3，此整除性不总是成立.设σ是集合｛1，2，…，n｝上的一个置换.如果存在σ，使得xσ（1）｜…｜xσ（n），则称S为一个因子链.Hong［10］证明了如果S为一个因子链，并且算术函数f∈CS：＝｛f｜（f*μ）（d）∈Z，这里d｜lcm（S）｝，那么在整数矩阵环Mn（Z）中，Smith矩阵（f（S））整除Smith矩阵（f［S］）.在2008年，Hong［11］证明了如果S为一个因子链且a｜b，则在整数矩阵环Mn（Z）中，（Sa）｜（Sb），（Sa）｜［Sb］和［Sa］｜［Sb］.但是如果ab，则上述整除性不再成立.设k为正整数.如果S可划分为，其中Si（1≤i≤k）为因子链，且满足1≤i≠j≤k，（max（Si），max（Sj））＝1，则称S由有限个互素因子链构成.谭千蓉等［14］证明：如果S由有限个互素因子链构成且1∈S，若a｜b，则det（Sa）｜det（Sb），det（Sa）｜det［Sb］和det［Sa］｜det［Sb］.

本文利用文献［12］中建立的定义在有限个互素最大公因子封闭集S上与算术函数相关联的矩阵的行列式的计算公式，首先给出了定义在有限个互素最大公因子封闭集S（1∉S）上GCD矩阵与LCM矩阵的行列式的计算公式，然后刻画了Smith矩阵（f（S））与Smith矩阵（f［S］）行列式之间的关系，最后给出了定义在有限个互素因子链集S上且1∉S时，幂GCD矩阵与幂LCM矩阵的行列式之间的关系.

1 主要结果及证明

本节给出本文的主要结果及证明.首先给出几个已知的定义和引理.

定义 1［6］对任意的x，y∈S且x＜y，如果x｜y且不存在其他的元素d∈S，使得x｜d｜y，则称x是y在S中的一个最大型因子.对与x∈S，用GS（x）表示x在S中的所有最大型因子构成的集合.

Hong［6］通过引入最大型因子概念，极大的化简了定义在最大公因子封闭集上的LCM矩阵的行列式的计算公式.

定义2［1］设S为正整数集，f为算术函数.对任意的x∈S令

定义3［12］设T是由不同的正整数构成的集合，f为算术函数.定义与集合T和f相关的函数如下：

定义4［12］设S由h个互素最大公因子封闭集S1，S2，…，Sh构成.S的极小元集M（S）定义为，其中min（Si）表示Si的最小元.

例如，若S＝｛2，5，6，8，11，35，143｝，则S由3个互素最大公因子封闭集构成且S的极小元集M（S）＝｛2，5，11｝.

引理5［6］设S为最大公因子封闭集，f为算术函数，则对任意的x∈S有

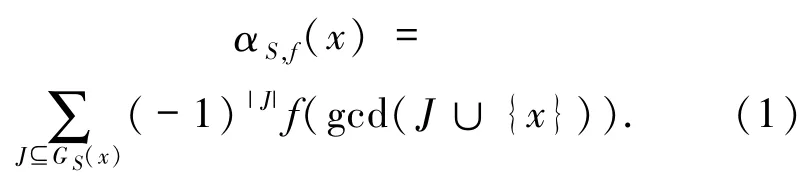
注1由定义1和2易知当S由多重互素GCD封闭集构成且满足1∉S时，（1）式依然成立.

引理6［12］设f为算术函数，设S由多重互素GCD封闭集构成且满足1∉S.M（S）表示S的极小元集，则

进一步，若f为乘法函数满足对任意的x∈S，有f（x）≠0，则

下面给出本文的主要定理及其证明.

定理7设S由多重互素GCD封闭集构成且满足1∉S.M（S）表示S的极小元集，则

其中I是算术函数，定义为I（n）：＝n.

显然，当S是因子封闭集时，由定理7可立即得文献［2-3］中的结果.若S＝M（S），则定理7即为文献［13］中的引理1.

定理8设S为多重互素最大公因子封闭集且满足maxx∈S｛｜GS（x）｜｝＝1，设f为乘法函数满足对任意的x∈S，有f（x）为非零整数且

f∈DS：＝｛f：f（a）｜f（b）这里GS（b）＝｛a｝｝.

（i）如果S至多由2个互素最大公因子封闭集构成，那么 det（f（S））｜det（f［S］）.

证明由假设，可设f（x）＝zxf（x*），其中zx是与x相关的正整数，设GS（x）＝｛x*｝.