椭圆曲线y2=(x-2n)(x2+2nx+m)的整数点
管训贵
(泰州学院 数理学院,江苏 泰州 225300)
0 引言
确定椭圆曲线的整数点是数论和算术代数几何学的重要问题之一,有关这方面的理论研究成果在现代科技中有着广泛的应用[1-6]。其中一类典型的椭圆曲线是
E(n,m):y2=(x-2n)(x2+2nx+m) ,
(1)
这里n为奇数,m为整数。
1987年,Zagier[7]提出了椭圆曲线E(1,31)的整数点问题;2009年,祝辉林和陈建华[8]运用代数数论和p-adic分析方法找出了E(1,31)的全部整数点;2010年,吴华明[9]运用有关Pell方程和二元四次Diophantine方程的解的性质,得到同样的结论。2014年,管训贵[10]证明了:若E(1,36s2-5)(原文中m=p为素数这一条件可忽略),这里s是使12s2+1以及6s2-1均为素数的正奇数,则椭圆曲线(1)当m=31时,仅有整数点(x,y)=(2,0)和(28 844 402,±154 914 585 540),当m≠31时,仅有整数点(x,y)=(2,0),从而推广了上述结果。2016年,过静[11]证明了E(-1,31)仅有整数点(x,y)=(-2,0)。2017年,杜先存、赵建红和万飞[12]证明了E(-1,36s2-5)(s满足文[10]中的条件)仅有整数点(x,y)=(-2,0)。
本文运用初等数论方法对E(n,m)给出以下一般性的结果。

1 若干引理
引理1 设s是正奇数,则方程x2-(144s2+12)y2=1有无限多组正整数解(x,y),其基本解是(x0,y0)=(24s2+1,2s)。
证明因为36s2+3≡7(mod8),所以36s2+3是非平方正整数,从而144s2+12也是非平方正整数。因此,方程x2-(144s2+12)y2=1有无限多组正整数解。此外,由于
(24s2+1)2-(144s2+12)(2s)2=1,
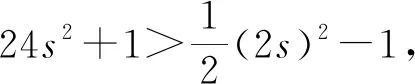
引理2 若D是一个非平方的正整数,则方程
x2-Dy4=1
(2)


通过对递归序列的讨论可得结论. 具体证明参见文献[13,定理1]。
由引理2立得:
引理3 方程x2-24y4=1仅有正整数解(x,y)=(5,1)。


证明分n为奇数,4|n以及n≡2(mod4)3种情形讨论。具体证明参见文献[14]。
引理5 若方程(2)恰有一组正整数解,则这个唯一的正整数解(x,y)可由下式表出:


(3)
n为正整数。

若n≡0(mod4),可设n=4m,则由(3)式可得

(4)


(5)



(6)




(7)

注意到k无平方因子,有k=2=n。证毕。
引理6 若D1和D2是适合D1>1以及gcd(D1,D2)=1的正整数,则方程
D1x2-D2y2=1
(8)
有无限多组正整数解,设(x0,y0)是(8)的最小正整数解,则(8)的全部正整数解由
表出,这里k是任意正整数。
证明设(u0,v0)是Pell方程
u2-D1D2v2=1
(9)
的基本解,(un,vn)是它的任一正整数解,则由
xn=unx0-D2vny0,yn=D1vnx0-uny0
(10)
所确定的(xn,yn)是方程(8)的解。事实上,我们有
D1(unx0-D2vny0)2-D2(D1vnx0-uny0)2=
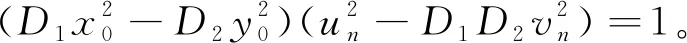
(11)
又方程(9)有无穷多组正整数解,故方程(8)也有无穷多组正整数解。
反之,若(xn,yn)是方程(8)的任一正整数解,则由(11)知(un,vn)是Pell方程(9)的解,
并且由(10)可解出un=D1x0xn+D2y0yn,vn=x0yn+xny0,故有
于是
由此可推出方程(8)的全部正整数解可表示为
这里k为任意正整数。证毕。
2 定理的证明
设(x,y)是(1)的任意整数点。因为m=36s2-8n2+3,|n|≤2s,所以x2+2nx+m=(x+n)2+m-n2>0。由(1)知x≥2n。当x=2n时,可得(1)的整数点为(x,y)=(2n,0)。
以下仅需考虑x>2n的情况。
令d=gcd(x-2n,x2+2nx+m),q=12s2+1为素数,这里s为正奇数,则m+8n2=3q,且d=gcd(x-2n,m+8n2)=gcd(x-2n,3q)=1,3,q或3q。
情形1若d=1,则由(1)可知,存在正整数a,b,使得
x-2n=a2,
x2+2nx+m=b2,
y=±ab, gcd(a,b)=1。
(12)
由(12)中第二个等式可得b2-(x+n)2=m-n2.因为m-n2是偶数,所以b与x+n必有相同的奇偶性,但此时2≡m-n2≡b2-(x+n)2≡0(mod4),矛盾。
情形2若d=3,则由(1)可知,存在正整数a,b,使得
x-2n=3a2,
x2+2nx+m=3b2,
y=±3ab, gcd(a,b)=1。
(13)
由(13)中前两个等式结合m=36s2-8n2+3可得3(a2+n)2+12s2-3n2+1=b2,因为12s2-3n2+1≡2(mod4),所以b与a2+n必同为奇数。但此时1≡b2≡3(a2+n)2+12s2-3n2+1≡3+12-3+1≡5(mod8),矛盾。
情形3若d=q,则由(1)可知,存在正整数a,b,使得
x-2n=qa2,
x2+2nx+m=qb2,
y=±qab, gcd(a,b)=1。
(14)
由(14)中前两个等式可得
(qa2+3n)2+m-n2=qb2。
(15)
将m=3q-8n2代入(15)式整理得
(q-3n2)a4+3(na2+1)2=b2。
(16)
当a是偶数时,由(16)式可知,na2+1与b必同为奇数,但此时1≡b2≡(q-3n2)a4+3(na2+1)2≡0+3≡3(mod8),矛盾;a是奇数时,由于q-3n2是偶数,故na2+1与b必同为偶数,但此时0≡b2≡(q-3n2)a4+3(na2+1)2≡-2+0≡2(mod4),矛盾。
情形4若d=3q,则由(1)可知,存在正整数a,b,使得
x-2n=3qa2,
x2+2nx+m=3qb2,
y=±3qab, gcd(a,b)=1。
(17)
由(17)中前两个等式可得
9(qa2+n)2+m-n2=3qb2。
(18)
将m=3q-8n2代入(18)式整理得
(3na2+1)2+(3q-9n2)a4=b2。
(19)
由(19)式知,a必为偶数。否则,当a为奇数时,b为偶数。但此时0≡b2≡(3na2+1)2+(3q-9n2)a4≡0-2≡2(mod4),矛盾。故设a=2c,这里c为正整数,代入(19)式可得
(12nc2+1)2+48(q-3n2)c4=b2。
(20)

(b+12nc2+1)(b-12nc2-1)=96rc4。
(21)
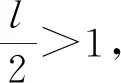
矛盾。由此可知l=2。
又因96r=25·3·r,故由(21)式可知,存在正整数f,g和t,使得
b-(12nc2+1)=tg4,
c=fg, gcd(f,g)=1。
(22)
这里t=2,6,16,48,2r,6r,16r或48r。
当t=2时,由(22)式可得,12nc2+1=24rf4-g4,取模3知,1≡-g4(mod3),不可能。

(12s2+1)(2f2)2-3(g2+2nf2)2=1。
(23)
令ξ=2f2,η=|g2+2nf2|,则(23)式成为
(12s2+1)ξ2-3η2=1。
(24)
易知(ξ,η)=(1,2s)为方程(24)的基本解。根据引理6,方程(24)的全部正整数解可表示为:
这里k为任意正整数。由此得方程(23)的全部正整数解(2f2,|g2+2nf2|)满足

(25)
将(25)式的右边展开可得
上式左边为偶数,右边为奇数,矛盾。
当t=16时,由(22)式可得,12nc2+1=3rf4-8g4,取模4知,1≡3rf4≡3f4(mod4),不可能。
当t=48时,由(22)式可得,12nc2+1=rf4-24g4.考虑到r≡2(mod3),对此式取模3知,1≡rf4≡2f4(mod3),不可能。
当t=2r时,由(22)式可得,12nc2+1=24f4-rg4,取模4知,1≡-g4(mod4),不可能。
当t=6r时,由(22)式可得,12nc2+1=8f4-3rg4,取模3知, 1≡2f4(mod3),不可能。
当t=16r时,由(22)式可得,12nc2+1=3f4-8rg4,取模4知, 1≡3f4(mod4),不可能。

(f2-6ng2)2-(144s2+12)g4=1。
(26)
由(26)式可知,方程
X2-(144s2+12)Y4=1
(27)
有正整数解
(X,Y)=(|f2-6ng2|,g)。
(28)
根据引理1,方程
x2-(144s2+12)y2=1
(29)
的基本解(x0,y0)=(24s2+1,2s)。又由引理2可知,方程(27)至多有一组正整数解(X,Y),比较方程(27)与(29)有:如果(X,Y)是方程(27)的正整数解,则方程(29)必有正整数解(x,y)=(X,Y2),因此,由(28)式可得

如果k=2,则
|f2-6ng2|=1152s4+96s2+1,
g2=4s(24s2+1)。
(30)
令g=2h,这里h为正整数,代入(30)的第二式得
s(24s2+1)=h2。
(31)
因为gcd(s,24s2+1)=1,故由(31)式知,存在正整数u,v,使得
s=u2, 24s2+1=v2,
h=uv, gcd(u,v)=1。
(32)
由(32)的前两式得
v2-24u4=1。
(33)
根据引理3,方程(33)仅有正整数解(u,v)=(1,5). 此时由(30)式和(32)式可得s=1,h=5,g=10,从而|f2-600n|=1 249.考虑到s=1时,n=±1,故有f=43,c=430。
此时a=860,r=5,q=13,可得(1)在s=1时仅有整数点(x,y)=(28 844 402,±154 914 585 540)适合x>2。

(24s2+1)k-2i-1·(2s)2i·(144s2+12)i。
(34)

3 结论