无角速度测量和饱和输入条件下航天器编队姿态有限时间跟踪控制
关启学,代 京,王伟光,姜月秋*
(1. 沈阳理工大学 信息科学与工程学院,沈阳 110159;2. 中国运载火箭技术研究院,北京 100076; 3.火箭军工程大学,西安 710025)
0 引 言
近年来,航天器编队飞行(Spacecraft Formation Flying)姿态跟踪控制问题由于其在深空探测等领域的广泛应用,引起诸多学者的关注。与传统的单航天器飞行相比,分布式编队飞行具有灵活性和模块化[1-4]等许多优势。
需要指出的是,对于实际条件下航天器姿态跟踪控制问题的研究具有很好的工程价值。如由于环境因素的影响,外部干扰总是不可避免的,这可能会降低系统稳定性,因此设计具有高精度和鲁棒性的姿态跟踪控制协议是一个具有挑战性的问题。
姿态跟踪控制意味着设计合适的控制协议使航天器能够以一定的精度跟踪上时变期望轨迹。文献[5]提出一种考虑动态不确定性和外部扰动的分布式自适应滑模控制协议,能够自适应保证航天器相对姿态和角速度在期望值邻域附近。文献[6]利用sigmod函数得到非线性延迟反馈控制律,解决了未知时滞条件下姿态跟踪问题。文献[7]提出一种新的切换角速度观测器,解决在无角速率测量情况下姿态跟踪控制问题。
基于上述分析,本文主要研究在无角速度测量、饱和输入和外部扰动的情况下航天器编队飞行的有限时间姿态跟踪控制问题。
1 问题建模
航天器姿态模型假设为刚体模型,使用改进Rodrigues参数(MRPs)描述航天器的刚体姿态运动。每个航天器的姿态运动学和动力学方程描述如下:

(1)
式中:n为飞行器的数量;Ji∈3×3为第i个飞行器的惯性矩阵;ui∈3×3为控制输入;di∈3为外部干扰;ωi∈3为相对于机体固定框架I的角速度;qi∈3为用于描述飞行器姿态的修正Rodrigues参数,定义为
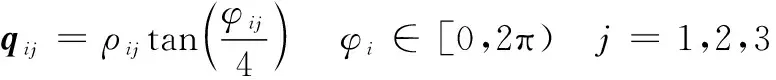
(2)
式中:ρi为欧拉轴;φi为欧拉角。用于姿态描述的MRPs的最大优点是可以对高达360°的特征轴旋转有效。符号×表示矩阵反对称算子,定义为
(3)
Ei∈3×3为文献[8]中给出的雅可比矩阵:
(4)
用类似文献[9]中的数学变换方法,式(1)可转换为
(5)

假设1:所有其他航天器都无法获得角速度; 每个航天器的态度,包括虚拟领航者和追随者,只能在局部领域内使用。

(6)
式中:c0为一个给定的正常数。
1.1 代数图论
对于多个刚体,信息可以在邻居成员之间传输,因此,通过有向/无向图描述信息流的语义是很自然的。令Γ={ν,ε,C}为一个无向图,其中ν={1,…,n}为节点的集合;ε⊂ν×ν为边的集合;C=[cij]为图Γ的加权邻接矩阵,节点i为第i个刚体,邻接元cij为第i个和第j个刚体之间的通讯关系,即(i,j)∈ε⟺cij>0。此时,节点i和j称为邻居,相应地,用Νi={j|(i,j)∈ε}表示节点i的所有邻居的集合。对于任意两个节点i和j,如果之间至少存在一条路径,那么就称图Γ是一个连通图。如果没有自循环重复边,则称图是简单的。通过使用图拓扑Γ,可以描述刚体之间的通信结构。
定义加权图Γ的拉普拉斯矩阵为
L=D-C
(7)


引理1[10]: 如果Γ={ν,ε,C}为一个无向连通图,那么拉普拉斯矩阵L为对称矩阵,其n个实特征值可以按升序排列:
0=λ1<λ2≤λ3≤…≤λn≤2dM
(8)

文中只考虑Γ的拓扑结构是简单和固定的,也就是说C是时不变矩阵。
1.2 有限时间状态观测器
为处理未知系统状态,一种可行的方法是设计观察者来近似其实际值。文献[11]中提到的扩展状态观测器(Extended State Observer,ESO)在完成非线性动态估计方面具有很高的效率,ESO将系统干扰视为扩展状态进行估算。在给出ESO前,需要有限时间的定义和引理。

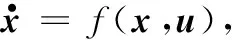
提出一种新的扩展状态观测器:

(9)
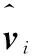
估计误差的有限时间收敛可以在以下引理中给出:

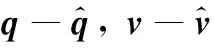
对于刚体姿态控制,一个显着的属性是“分离属性”,详细证明见文献[7]。
2 主要结果

2.1 姿态跟踪误差系统
为了便于分析,引入两种状态变量来测量每个航天器的绝对和相对状态误差。绝对状态误差是第i个航天器的姿态和姿态速度跟踪误差,与虚拟领航者(期望轨迹)有关,其定义如下:

(10)
将式(10)调用到式(5),可得到姿态跟踪误差动态系统:

(11)
定义:

那么,式(11)可以用矢量形式表示:

(12)
邻居成员之间的系统状态相对错误可定义为

(13)
定义αi1,αi2,αi3∈3为第i个航天器的整体跟踪误差,可以写为
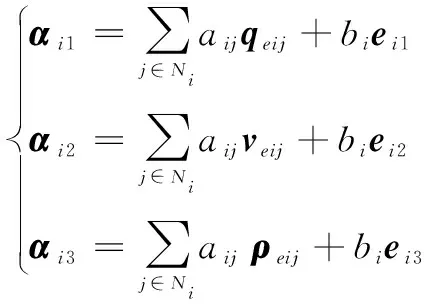
(14)


(15)
定义:
集中态度跟踪误差可以表示为

(16)
式中:M=(L+Β)⊗I3∈3n×3n。由于有向图有一个生长树,所以L+Β是可逆的。因此,α1和α2的动力学方程可以用矢量形式写为

(17)
滑动模式变量si=δαi1+αi2,其中δ为正常数参数。那么,si对于时间求导,即


(18)
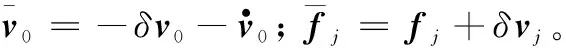
定义:
则式(17)可以写为
(19)
2.2 控制协议设计和稳定性分析
第i个航天器的滑动模式控制协议为
(20)


(21)

(22)
定理1: 考虑式(9)、式(20)和假设1~2得到满足,滑动流形将会聚到该区域:

(23)
证明: 考虑以下Lyapunov函数候选项:
(24)
对式(24)两侧进行微分并集成式(20),可以得到Lyapunov函数的时间导数:

(25)
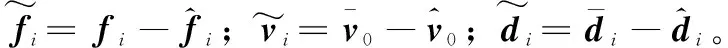
(26)

(27)

(28)
(29)
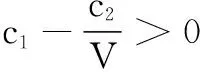
(30)
(31)

证明完成。
从式(28)~(29)可知,滑动流形s会在无限时间Tf收敛到范围Θ中。此外,从式(30)可知,M的特征值决定了参数Θ的大小。
2.3 具有输入饱和度的姿态跟踪的滑动模式控制
在实际工程中,输入饱和度作为最重要的非平滑非线性应该在控制设计中明确考虑。因此,提出姿态跟踪系统方程式(1)的滑模控制,在该部分存在未知非对称输入饱和、外部干扰和无角速度测量。考虑未知输入饱和约束,控制输入ui由下式给出:
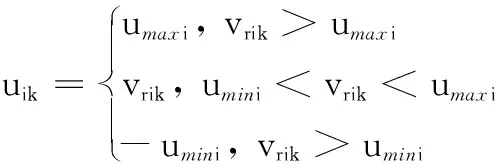
(32)
式中:vrik为设计好的控制输入命令,且k=1, 2, 3;umini和umaxi为控制输入饱和度的未知参数,umini≠umaxi表示非对称输入饱和度。
为了进一步分析未知非对称输入饱和的影响,式(1)可以转换为

(33)

(34)
考虑式(34)和式(12),得到
(35)
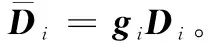
由于未知的复合扰动Di,式(17)被修改为
(36)
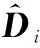
基于有限时间观测器的输出,将滑动模态姿态跟踪控制设计为
(37)
式中: 0<α<1;ki1>0;ki2>0。
上述设计过程和分析可归纳为以下定理,其中包含具有未知非对称输入饱和度的姿态跟踪控制动力学方程式(1)的结果。
定理2:考虑具有外部干扰和饱和输入的姿态跟踪动力学方程式(1)和无角速度测量,有限时间观测器被设计为式(36)。在所提出的滑模跟踪控制表达式(37)下,所有航天器的姿态跟踪误差可以在有限时间内收敛到有界区域。
3 数值仿真
为了验证上述方法的有效性,给出一个多航天器编队的仿真算例来说明。假设编队是由6个航天器c1,c2,c3,c4,c5,c6以及一个虚拟领航者l共同组成, 成员之间的通信拓扑结构关系如图1所示。

图1 编队通信拓扑结构
这里认为两个航天器之间存在通讯关系, 则其拓扑权重大于0,否则为0。由此,可以假设整个航天器编队的权重邻接矩阵Α和Β分别为

(38)

(39)
式中:Α表示编队成员之间的通讯拓扑连接关系;Β代表虚拟领航者l与编队成员之间的通讯连接关系。
假设航天器为刚体,其惯性矩阵为[15]



为了用式(26)进行模拟,饱和输入满足umini=5,umaxi=10,每个航天器的初始状态(即姿态和角速度)为
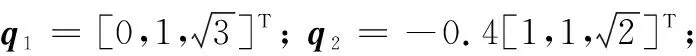


w1=[1,2,3]T;w2=[2,1,3]T;
w3=[0.9,1.6,1.3]T;w4=[2,1.5,1.2]T;
w5=[1.1,2,2.1]T;w6=[2,1,1.8]T。
每个航天器的正弦波扰动如下:
d1(t)=0.1[sin(t),cos(t),sin(2t)]T;
d2(t)=0.1[sin(2t),cos(2t),sin(4t)]T;
d3(t)=0.1[sin(3t),cos(3t),sin(6t)]T;
d4(t)=0.1[sin(4t),cos(4t),sin(8t)]T;
d5(t)=0.1[sin(5t),cos(5t),sin(10t)]T;
d6(t)=0.1[sin(6t),cos(6t),sin(12t)]T。
航天器所需的时变姿态是相同的,由下式给出:
(40)
控制增益和观察者参数为ki=2,α1=0.8,α2=0.6,α3=0.4,β1=1.25,β2=1.05,β3=0.65。
根据上述初始条件,对航天器姿态运动进行仿真计算,结果如图2~3所示。

图2 航天器跟踪角度与时间的关系

图3 滑模面与时间的关系
从图2可看出,在编队控制初期,各航天器的飞行姿态比较杂乱无章,但在控制器作用下,大约4 s左右,各飞行器的姿态趋于一致。说明即使存在外部干扰、饱和输入以及无角速度量测等情况,本文设计的方法依旧可以保证飞行器姿态在较短时间内达到期望的跟踪状态,实现了既定的目的。
图3表明滑模变量随着时间的变化关系。从图中可以看出,在控制器的作用下,系统滑模变量4 s左右收敛到0域附近,实现了编队成员之间相对状态误差趋于0。
4 结 论
为了解决复杂约束条件(无角速度量测、外部扰动、饱和输入等)下的航天器编队姿态协同控制问题,本文提出了一种分布式滑模控制协议。通过数学转化将未知非对称饱和输入与外部扰动合并为复合扰动,通过设计有限时间观测器来实时估计航天器姿态速度和外部扰动; 利用Lyapunov函数从理论上证明了所设计方法的有效性。文章最后的算例对设计方法进行了仿真验证。
需要指出的是,在实际工程领域,无角速度量测、外部扰动、饱和输入等条件均是实际飞行器编队过程中需要克服的约束。因此, 本文所考虑的约束条件与工程实际贴合比较紧密,具有较强的工程指导意义。后续还需要进一步考虑编队成员之间的时延、丢包等约束条件对控制效果的影响。

