基于摩擦补偿和自抗扰的惯导测试转台复合控制

朱海荣，吴 瑜，张先进，李 奇

(1.江苏工程职业技术学院 机电工程学院, 江苏 南通 226007; 2. 东南大学 自动化学院, 南京 210096)

0 引 言

为了提高惯性导航设备投入运行后的成功率，降低在实际运行过程中的风险，投入运行之前的仿真和测试必不可少。专业的测试转台可以模拟各种姿态(包含速度、加速度和姿态位置等信息)，对惯导系统进行全方位的性能测试，为惯性导航技术的发展提供有力保障[1-3]。惯导测试转台在高、低速运行以及转向过程中会受到轴系间摩擦的影响，系统在运行过程中模型参数也会发生变化，如果控制器设计不合理，难以取得良好的控制性能，甚至会导致系统不稳定，严重影响测试效果[4-5]。如何设计合理的控制器，对系统所受到的各种干扰进行有效的补偿，提高惯导测试转台的控制性能，具有重要的理论研究价值和实际工程意义。

惯导测试转台存在轴系摩擦、轴系框架不正交、轴系耦合以及其他机械和电气方面诸多干扰因素的影响，经典控制方法难以对系统中的各种非线性因素进行针对性的补偿，不能获得满意的控制效果[6-7]。非线性摩擦干扰力矩作为测试转台的重要影响因素，近年来获得了国内外学者的广泛关注，在非线性摩擦补偿方面取得了一系列的研究成果。基于模型的摩擦补偿： 首先通过辨识得到系统的摩擦模型，在此基础上对摩擦进行前馈补偿。无摩擦模型的补偿： 不依赖于精确的摩擦模型，把摩擦干扰力矩当成外部扰动，通过扰动抑制算法对摩擦进行补偿，主要有高增益PD算法、变结构控制算法和基于观测器的控制算法[8-10]。此外，神经网络、自适应控制、模糊控制等智能控制算法也在摩擦补偿方面得到了大量的运用，由于计算量较大，很多复杂的智能控制算法尚处于仿真研究阶段，在实际应用中都对算法进行了针对性的简化处理[11-12]。

本文提出一种结合摩擦补偿和自抗扰控制技术(active disturbance rejection control, ADRC)的复合控制方法： (1) 用LS算法辨识转台系统的Stribeck摩擦模型，将其作为前馈补偿加入到控制中； (2) 上述LS算法并不能辨识出系统精确的摩擦模型，所进行的前馈补偿也只是对实际摩擦的部分补偿，故设计了自抗扰控制器，利用扩张状态观测器对系统输出进行状态和扰动估计，以降低对摩擦的过补偿、欠补偿和系统模型失配等其他干扰因素的影响[13]。

1 测试转台数学模型

(1)

式中：Km为电机的力矩系数；J为转动惯量；b为黏性阻尼系数；Ff为以摩擦为主的干扰。

2 摩擦前馈补偿

2.1 LS算法基本原理

考虑到算法的工程实用性，采用LS法对系统的摩擦模型进行辨识。其基本原理： 给定一个参数，首先计算模型的状态变量和模型的观测向量，并将观测值与系统的实际输出值进行比较，求出两者差值的平方和，再以某种计算法则不断地改变参数的值，当所求出差值的平方和最小时，即可认为该参数值为实际系统参数的近似值[14-15]。考虑模型：

M=f(x)+ζ

(2)

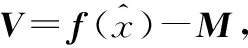
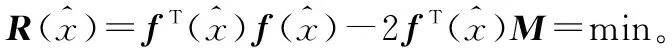
x(1)=x(0)+(BT(x(0))B(x(0)))-1BT(x(0))

(M-f(x(0)))

(3)

进一步地，以x(1)为近似值进行迭代:

x(k+1)=x(k)+(BT(x(k))B(x(k)))-1BT(x(k))

(M-f(x(k)))

(4)

2.2 摩擦模型辨识

Stribeck摩擦模型对静摩擦、临界润滑、部分润滑和完全润滑阶段的描述都较为准确，其数学表达式为

(5)

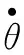
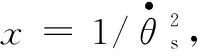
表1 LS算法辨识所得Stribeck摩擦模型参数

在进行摩擦前馈补偿时，选取Stribeck摩擦模型为

(6)

2.3 摩擦前馈补偿算法设计

图1 基于摩擦模型的前馈补偿控制算法示意图

3 自抗扰控制器设计

ADRC是由PID控制所演变过来的一种控制算法，吸取了PID “误差反馈控制”的核心理念，不依赖于对象的精确数学模型，仅需知道对象的阶次，由于其实用性较高，在伺服控制、飞行器姿态控制、电力系统等领域得到了广泛的应用[16-18]。ADRC包含三部分： 跟踪微分器(TD)，扩张状态观测器(ESO)和非线性状态误差反馈控制律(NLSEFL)。TD用于安排过渡过程、给出控制信号，即使不用积分环节也能实现无静差，有效避免了积分反馈带来的副作用，从而解决快速性和超调之间的矛盾。ESO用于观测扩展出来的状态变量，对未知扰动和系统未建模部分进行估计[14]。在设计中，可以把系统的不确定项当作系统内部扰动，和系统受到的外部扰动一起，当作系统的总扰动，通过合理的ESO把上述总扰动估计出来。NLSEFL利用广义误差来构造非线性状态误差反馈控制律。由于ESO和NLSEFL不依赖于被控对象的具体数学模型、也不依赖于扰动的具体形式，使非线性控制律具有很好的适应性和鲁棒性。

ADRC的具体设计步骤如下，若存在系统：

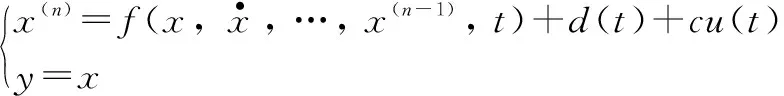
(7)

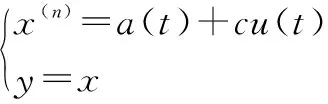
(8)

设计自抗扰控制器结构如图2所示。图中，V(t)为系统参考输入，v1， …，vn为V(t)的跟踪信号及各阶导数的跟踪信号；z1，…，zn为扩张状态观测器的状态估计；zn+1为扩张状态观测器对系统总扰动的估计；ε1，…，εn为误差； 利用跟踪微分器和扩张状态观测器对应输出量之间的误差，采用适当的非线性反馈控制率得到控制量u0(t)。

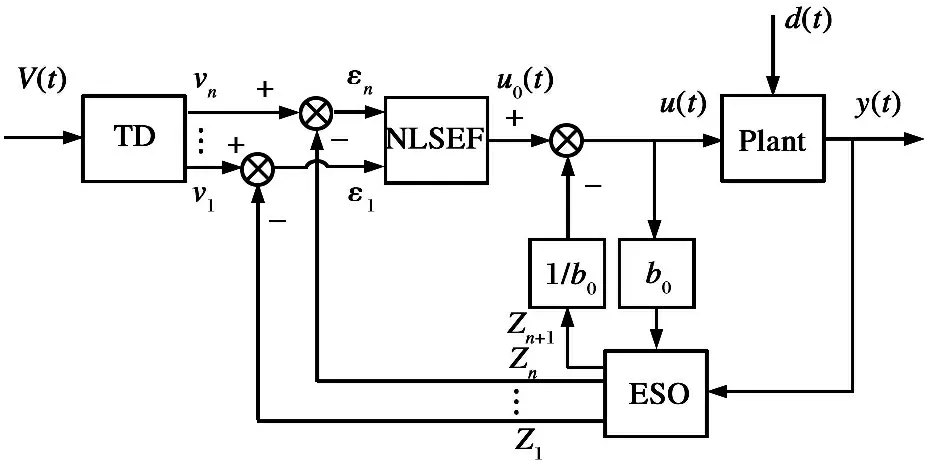
图2 自抗扰控制器结构示意图

非线性跟踪微分器的一般形式为

对于高校层面来说，要将人才培养的规模扩张逐渐向优化人才培养结构方面转化，需要克服扩张规模的冲动，要根据自身学科的基础以及所具有的办学条件，充分结合当地的经济产业结构以及政府的人才规划来优化人才培养的结构，培养多样化、复合型的人才，这是值得深度思考以及认真研究去解决的课题。作为高校，首先要有这方面的整体考虑，作为思想基础，以后才有可能去采取措施来切实地保障优化结构的目标实现。

(9)

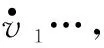
选取扩张状态观测器：

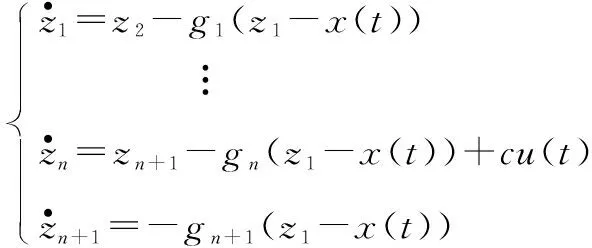
(10)

定义广义误差为

ε1=v1-z1,ε2=v2-z2, …,εn=vn-zn

(11)

对广义误差进行非线性组合，得到非线性状态误差反馈控制器：

u0=β1fal(ε1,α,δ)+…+βnfal(εn,α,δ)

(12)

(13)

根据广义误差的非线性组合和模型与外扰的补偿，可得控制量：

u(t)=u0(t)-zn+1(t)/c

(14)

式中： -zn+1(t)/c起扰动补偿的作用。

4 摩擦补偿+自抗扰控制器设计

本文利用LS算法对摩擦模型进行辨识，并将其作为前馈补偿加入到控制器中，由于在建立系统数学模型和摩擦模型的过程中难免存在误差，同时系统还受到多种未知的外部干扰，所以仅用摩擦前馈补偿是不够的，可利用自抗扰控制器的ESO对未知扰动和系统未建模部分进行估计，形成摩擦补偿+自抗扰控制的复合控制算法。

在ADRC设计中，其控制量式(14)对扰动进行了补偿，故可以将非线性系统式(7)的控制问题近似退化为一个n阶线性积分串联型系统x(n)≐bu0(t)的控制问题，设计中可以直接使用线性比例函数来设计NLSEF，从而简化ESO的结构，同时保留ADRC的优良性能。

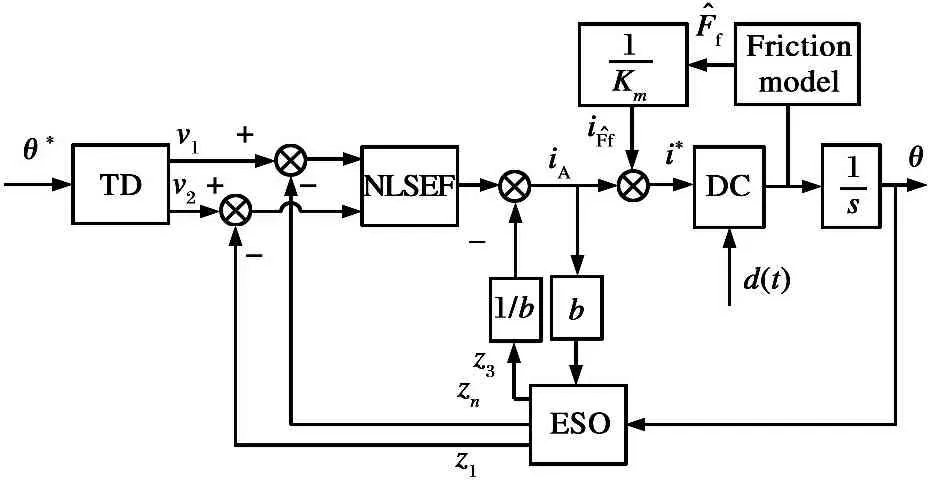
图3 基于摩擦补偿和自抗扰控制方案结构示意图

测试转台伺服单元自抗扰控制器的跟踪微分器为

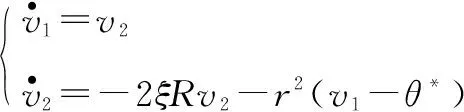
(15)

式中：v1为对给定角度信号θ*安排的过渡过程；ξ为阻尼系数；r为可调参数。

测试转台伺服单元自抗扰控制器的扩张状态观测器：

(16)

式中：z1，z2为对实际位置θ及其微分的估计；z3为扰动估计； -p为期望闭环极点。

测试转台伺服单元自抗扰控制器的线性反馈控制率如下：

(17)

式中：Kp，Kd分别为ADRC的比例和微分增益，均大于0。

关于ADRC的稳定性，邵立伟和陈增强分别在文献[19-20]进行了推导证明，此处不再另外描述。

5 实验分析

惯导测试转台实验系统如图4所示。最外围的“U形+O形”两个轴系为惯导测试转台，内部两个O形轴系用于安装被测惯性器件。根据测试要求，外围的“U形+O形”两个轴系可以分别提供方位和俯仰两个方向的摇摆信号，用于模拟载体运行姿态。惯导测试转台实验系统主要由伺服控制模块、驱动模块、运动信号测量模块和人机交互显示模块构成。以U形方位摇摆轴为例，综合考虑轴系的转动惯量(含负载)和直流力矩电机所需要的加速度，选择了J160LYX105型直流力矩电机，电机参数见表2。

图4 某测试转台实物图

表2 方位轴电机参数

首先计算方位摇摆轴的转动惯量，采用新一代机械设计CAD系统Solid Edge 6.0对其进行建模，方位摇摆轴系主要包含如下零部件： 方位轴主轴、方位轴轴承、方位轴力矩电机转子、方位轴测速机转子、方位轴旋转编码器转子和方位轴光电盘、外部U形框架、内部O形框架(包括安装在O形框架里面的被测试对象)，经计算可以得到方位摇摆轴转动惯量为8.65 kg·m2； 电机的力矩系数Km=Tfd/Ifd(Tfd为电机的峰值堵转转矩;Ifd为电机的峰值堵转电流)，由表2得Km= 2.4 N ·m/A。

测试转台伺服单元的电流环都采用PI控制，速度环分别采用基于摩擦补偿的PI控制(PI+ Friction Compensation，PI+FC)和本文所提出的基于摩擦补偿的自抗扰控制(ADRC+ Friction Compensation，ADRC+FC) ，均选取式(5)所示的摩擦模型。为了比较的公平性，把控制器的参数都调到各自的最优状态。PI+FC控制控制器参数为：kp=500，ki=60； ADRC+FC控制器参数为：kp=800，kd=40，r=1 500，b0=b=Km/J=0.277 5，ESO的极点-p=-2 500。

给定幅度为3°的正弦指令信号，采样时间为20 s，PI+FC和ADRC+FC控制的响应曲线以及两种控制下的误差放大曲线分别如图5所示。图5(c)中，经对比发现： 采用ADRC+FC控制时的最大误差接近0, 3°，采用PI+FC控制时的最大误差在0, 15°左右，ADRC+FC的控制效果较好; 采用两种控制策略的最大误差均出现在系统换向时，这主要是由非线性摩擦力矩导致的。FC前馈补偿能对摩擦力矩起到部分补偿作用，但是摩擦建模中难免存在误差，而且除了摩擦，测试转台伺服单元还受到多种未知外部干扰的影响，仅用摩擦前馈补偿是不够的。故在摩擦补偿的基础上设计了自抗扰控制器，利用ESO对系统输出进行状态和扰动估计，以降低摩擦补偿不充分、系统模型失配及其他干扰因素的影响。

6 结 论

综合摩擦补偿和自抗扰控制两者的优点，设计了基于摩擦补偿+自抗扰控制的测试转台复合控制算法： 一方面用LS算法辨识系统的摩擦模型并进行前馈补偿，一方面用自抗扰控制器中的ESO观测出系统建模误差带来的不确定性、摩擦补偿过程中的过补偿、欠补偿和其他未知外界扰动，并用此观测值进行补偿，降低了摩擦前馈补偿对摩擦模型及摩擦模型辨识精度的要求。仿真和实验结果表明，ADRC+FC控制适合于测试转台这类特殊的存在摩擦以及未知扰动的伺服控制系统，具有较高的工程应用价值。

图5 正弦响应曲线