双燃速无喷管助推器内弹道性能优化研究
郝 雯,张磊扬,孙振华,周 磊
(中国空空导弹研究院,河南 洛阳 471009)
0 引 言
整体式固体火箭冲压发动机一般采用内置助推器加速,以便达到冲压发动机有效工作的飞行速度。无喷管助推器可省去传统助推器的喷管抛落系统,消除了抛出物对载机和阵地的危害,且可靠性高、研制成本低,近年来在固冲发动机研制中逐渐得到应用。
国内对无喷管助推器研究起步较晚,在内弹道性能研究方面,胡建新等人[1]对整体式固体火箭冲压发动机的无喷管助推器内弹道进行了计算。曹任刚[2]给出了一种无喷管固体火箭发动机内弹道计算方法。现行研究采用的内弹道计算模型所涵盖的工作范围和预示精度均具有较大的局限性,仍需进一步改进。
针对无喷管助推器的装药方案,曹任刚[3]研究出采用高能装药、高燃速装药、优化装药结构、合适的装药燃速压强指数、两种燃速装药串联等方式,有利于对无喷管发动机性能的提高。丁林等人[4]研究了两种不同燃速推进剂组成的组合式药柱助推器性能,并对分段、分层组合药柱方案进行对比分析,说明了双燃速组合方案能增加壳体强度的利用率,有效提高比冲。双燃速无喷管助推器的应用一方面扩展了装药方案的设计参数种类及范围,另一方面,也对性能优化提出了挑战。黄礼铿等[5-6]采用简化的一维非定常计算模型,对圆柱内孔装药无喷管助推器的药柱结构进行优化设计研究。由于无喷管助推器内弹道性能影响因素多、耦合关系复杂,在全局最优求解过程中需综合考虑数值计算精度与效率。
综上,在建立更为全面和精确的无喷管助推器内弹道性能计算模型的基础上,采取合适的优化策略,得到满足各种约束条件的最优装药设计方案,对解决无喷管助推器性能提升问题具有重要意义。对此,本文建立了考虑两相流动的一维非定常内弹道计算模型,并通过数值计算获得关键因素对内弹道性能的影响规律及敏感程度,为装药设计和优化提供指导原则和数据支撑。在此基础上,利用智能优化数值算法,提出了一种无喷管助推器装药结构全局最优设计方法。
1 一维非定常内弹道计算模型
双燃速无喷管助推器的性能计算涉及到两相流动和复杂的燃烧机理。综合考虑计算的有效性和可执行性,本文计算模型采用如下假设: (1) 所有的化学反应都发生在薄平面区域的推进剂表面; (2) 燃烧室内的流动是一维的; (3) 在推进剂表面的燃烧过程是准稳态的,点火瞬时完成; (4) 燃气与点火器产生的气体为同一性质气体; (5) 燃烧产物两相平衡,无粘性,遵循理想气体方程。
基于上述假设,对于采用双流体模型的一维两相流动,其控制方程为
(1)
其中,参数项Q、通量项F及源项S分别为
(2)

状态方程为
P=ρRT
(3)
式中:R为气体常数;T为温度。
式(2)中的源项分别为
(4)
式中:ρs为推进剂密度;H为推进剂热值;ε为气相质量分数。
由于无喷管助推器工作过程燃烧的非定常特征和侵蚀燃烧效应均较为显著,所以在燃速计算过程中,采用考虑初温效应和侵蚀燃烧的King[7]模型燃速公式:
(5)
式中:r0为无侵蚀作用下初温为T0时的燃速;σp为温度敏感系数;a为侵蚀系数;G=ρu;G0为临界质量流率;m为指数常数;u为平行于燃面的燃气流速;c为声速。
为验证所建立的一维非定常内弹道计算模型的准确性,将该模型计算数据与某φ203无喷管火箭发动机原理样机的试验数据进行对比。根据同类推进剂特性,临界质量流率G0为140.6 kg/(s·m2),侵蚀模型系数σp,a,m分别取0.05%,6.1×10-4,0.8。
表1为性能指标的对比结果,其中除最大推力及最大压强偏差在6%左右外,其他性能指标偏差均在4%以下。图1为发动机推力和压强曲线的对比,可见二者曲线吻合度较好。

表1 φ203发动机仿真及试验性能指标

图1 φ203发动机推力、压强时间曲线
类似地,对某φ130全尺寸无喷管火箭发动机原理样机的模型计算与试验数据进行对比。结果表明,计算数据与试验数据曲线吻合度较好,且各性能指标偏差均在4.7%以下。
经过多次计算与试验数据对比,本文采用的无喷管助推器一维内弹道计算模型与算法程序,数值计算偏差基本在3%左右,适用于助推器的内弹道性能分析,能够较为准确地描述无喷管助推器装药结构对发动机性能的影响。
2 关键参数影响规律分析
无喷管助推器实际上就是一台固体火箭发动机,其没有专门的喷管分组件,而是由药柱通道起到使燃气流加速和膨胀的作用。当前为适应战术需求,导弹总体对发动机的长径比提出了限制。为保证发动机比冲等性能指标,助推器可通过采用双燃速装药方案来提高装药能量的转化效率,进而提高比冲。
对于双燃速无喷管助推器,装药形状主要由以下参数决定: 装药长度、高低燃速装药长度、扩张段长度、扩张角、装药界面倾角、内孔扩张半角、装药内径和装药外径。其中,装药长度、外径及内径由发动机结构参数约束,故在内弹道优化时不予考虑。针对影响发动机效率的五个关键参数,通过试验设计方法(DOE)进行全因子矩阵设计,获取输入参数与输出参数之间的关系和趋势,可掌握其对内弹道性能的影响规律及敏感度。
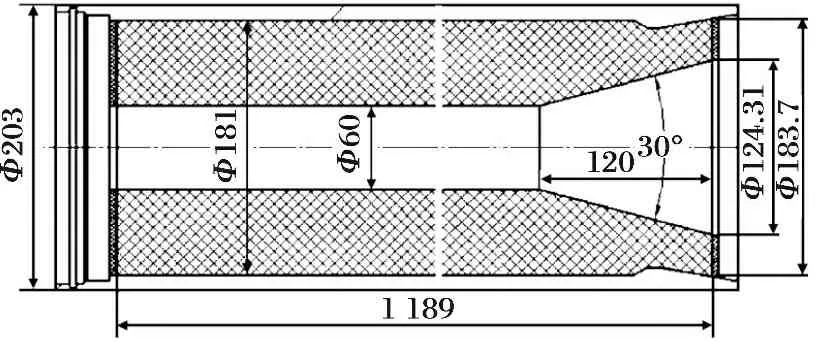
图2为基础药型和五个关键因素示意图。在实际设计过程中,根据各参数物理意义和设计经验,设定了相应取值范围,如表2所示。其中装药总长为1 189 mm,装药外径及内径分别为φ181 mm、φ60 mm。

图2 关键因素示意图

表2 基础药型参数
2.1 比冲随扩张角α变化
采用DOE试验设计方法,分析扩张角α在40°~60°范围内取值时对发动机比冲的影响,并将所得数据以40°扩张角下的结果为基准,进行归一化处理,可得到发动机比冲随扩张角的变化趋势曲线,如图3所示。
可以看到,比冲随扩张角的增大而增加,当扩张角增大至60°时,比冲增加2.16%。经分析可知,实际工作过程中,随着扩张角的增大,低燃速药所形成的喷管型面越扩张,燃气流动速度越快,能量发挥更充分,比冲也会随之增加,与仿真计算结果相符。
2.2 比冲随装药界面倾角β变化
图4为发动机比冲随装药界面倾角的变化趋势,其中数据均以0°装药界面倾角下的结果为基准进行了归一化处理。
现在国内的无喷管助推器高低燃速界面均为竖直界面,即界面倾角β为0°。若界面为倾斜界面时,助推器点火后,随着燃面的退移,低燃速装药与高燃速装药的倾斜界面将会形成一个“天然”的自然过渡的喷管造型,这样燃烧通道内的压强增大,装药燃速也会提高,比冲也随之增大。图中β从0°增大至5°时,比冲增加3.91%,比冲的显著增大也印证了这一分析,之后随着装药界面倾角继续增大,比冲也随之增加。
2.3 比冲随内孔扩张半角γ变化
图5为发动机比冲随装药内孔扩张半角的变化趋势,其中数据均以0°内孔扩张半角下的结果为基准进行了归一化处理。
随着内孔扩张半角的增加,比冲逐渐降低,当内孔扩张半角为1°时,比冲下降了4.68%。分析可知,随着内孔扩张半角的增加,装药通道直径增大,发动机压强降低,比冲也随之降低。
2.4 比冲随扩张段与低燃速段长度之比变化
为保证喷管喉部装药结构完整性,一般取Le 图3 比冲随扩张角α变 化的趋势Fig.3 The trend of spe-cific impulse varies with α图4 比冲随装药界面倾 角β变化的趋势Fig.4 The trend of spe-cific impulse varies with β图5 比冲随内孔扩张半 角γ变化的趋势Fig.5 The trend of specific impulse varies with γ图6 比冲随Le/L2变化 的趋势Fig.6 The trend of specific impulse varies with Le/L2 通过DOE试验设计可辨识出关键的试验因子,提高设计的稳定性。通过方差分析,可得到试验因子在所有试验中响应的平均值,即主效应。输出的Pareto图可反映出试验因子对响应的贡献程度百分比。图7为五个关键因素对比冲影响的主效应图,与前文分析的趋势相同。其中比冲与装药界面倾角、低燃速段长度、扩张角成正向比例关系,随扩张段长度成先增后减的关系,随内孔扩张半角成负向比例关系。 图7 参数对比冲的影响主效应 图8为五个关键因素对发动机比冲的影响贡献程度百分比。可见装药界面倾角变化对比冲的影响最大,高达到50%,而扩张段长度变化对比冲的影响最小,为负效应约-3%左右。 图8 参数对比冲的影响贡献度 综合以上分析,可以得出双燃速无喷管助推器装药设计应当遵循的几点原则: (1) 高低燃速装药界面建议增加倾角,可以减小燃气通道壅塞截面扩大的速率,保持“天然”的自然过渡的喷管造型,从而使压强曲线的下降幅度有一定程度的减小,有效提高比冲。 (2) 在保证装药尾部厚度足够、燃烧过程中不脱落的情况下,适当增大扩张角,可有效提高喷管出口速度,提高发动机比冲。 (3) 在装药设计时必须综合考虑比冲及头部最大压强的影响,合理设计内孔扩张半角、低燃速段长度及扩张段长度。 针对无喷管助推器内弹道性能影响因素多、耦合关系复杂的特点,本文提出一种无喷管助推器装药结构及参数选型全局最优设计方法,即在掌握关键参数影响规律及敏感度的基础上,利用前文所述数值计算方法确定无喷管助推器药柱参数与内弹道性能之间的相互关系,然后通过优化搜索方法获得满足设计要求的最优设计解,其流程示意图如图9所示。 图9 优化流程示意图 传统的梯度优化和直接搜索等数值优化方法无法找到全局优化解,而遗传算法和模拟退火算法等基于全局探索的优化方法更能找到全局最优解,但也存在着收敛速度慢,计算效率低的缺点。因此结合全局优化方法与数值优化方法的优点,进行组合优化,逐步成为工程优化设计领域的新趋势。 基于无喷管助推器内弹道性能计算的特点,本文选用Pointer智能自动优化算法。其基本思路为: 首先使用遗传算法进行全局寻优,判断优化空间的性质和最优解所在区间,然后在此区间内依据所优化问题性质,选择最合适的数值优化算法,如序列二次规划法等,以提高计算效率,从而可以加速优化进程,形成一个最优的组合优化策略。 依据前文中各关键参数对于发动机性能优化目标的影响以及已有的设计经验,本文选取文献[2]中的单燃速助推器方案为基础方案,以比冲最大作为优化目标进行优化设计,同时对喉部残药进行约束,以保证无喷管助推器的安全工作,如图10所示。 图10 装药基础方案 采用本文提出的方法进行优化设计,得到的无喷管助推器药柱结构及设计参数如图11和表3所示。优化后采用高低两种燃速的装药方案。尾部扩张角增大至59°,高燃速装药与低燃速装药为倾斜过渡界面,倾角为5°,内孔扩张半角为0°,扩张段长度与低燃速装药长度之比为0.90。 图11 优化后的双燃速装药方案 表3 优化后的双燃速装药结构参数 将优化前后的方案及设计参数作为输入进行仿真计算,从而得到对比验证结果,助推器的推力/时间、压强/时间曲线如图12所示。单燃速无喷管助推器的工作特点是工作初期压强峰值较高,压强时间曲线呈单调下降趋势。同时由于“喉径”在不断扩大,燃面不断增加,推力曲线基本保持平直。而优化后采用双燃速装药方案,尾部装填低燃速推进剂,限制了喉径减小速率,燃烧室压强曲线基本保持平直趋势,平均压强大幅提高,同时可使推力不断增加。另外,燃烧室内一直保持较高的压强,增加了壳体强度的利用率,有助于发动机比冲的提高。 图12 优化前后的助推器推力和压强曲线对比 表4列出了优化前后的性能指标结果,通过优化, 比冲从1 995.17 N·s/kg增加至2 233.23 N·s/kg,增幅为11.8%。最大推力增加68.99%,并且在装药量下降4.5 kg的基础上,总冲仍保持1.33%的增长。 表4 优化前后的助推器性能指标对比 (1) 本文建立的无喷管助推器一维非定常内弹道计算模型和相应数值计算方法,适用于双燃速无喷管助推器装药结构的内弹道性能分析,在优化设计中能够较为准确地描述装药结构对发动机性能的影响。 (2) 通过数据分析,掌握关键参数对双燃速无喷管助推器内弹道性能的影响规律和敏感度,可为助推器优化设计方案提供性能数据参考,为装药结构优化设计提供选型支持。 (3) 提出一种无喷管助推器装药结构及参数选型全局最优设计方法。经验证,通过智能优化算法进行全局寻优设计,优化后方案较基础方案的比冲增加11.8%,同时在装药量下降4.5 kg的基础上,总冲仍保持1.33%的增长,实现了在约束条件下显著提升无喷管助推器性能指标的目的。
2.5 讨 论


3 无喷管助推器药型结构优化设计

3.1 优化方法
3.2 优化目标
3.3 优化结果




4 结 论

