以模型为例 探究几何最值问题
张海霞
摘 要: 在初中数学中,常常遇见求解几何最值的问题,由于这类题型的综合性强,形式灵活多变,知识点涉及广泛,学生常常束手无策.想要掌握这类题目并不难,需要学生把握好常见的类型,透过现象看本质,深度挖掘题目背后的知识点,再结合相关知识来进行转化,就可以化繁为简了.本文就初中数学几何最值问题的探究做出详细的思路分析,并且提出相关的学习建议.
关键词: 初中数学;几何最值;模型;合理转化
中图分类号: G632 文献标识码: A 文章编号: 1008-0333(2021)35-0034-02
一、“将军饮马”模型解读 几何最值问题的形式灵活多变,但是它之间蕴含的基本模型是一定的,模型如下:
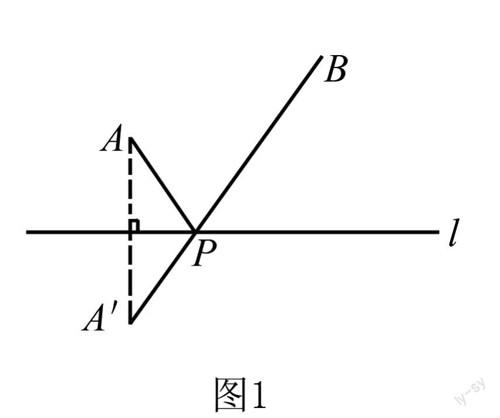
模型满足的条件:如图1所示,有一条已知直线l和直线外两点A、B,并且点A、B在直线l的同一侧,点P为一个动点,它只能在直线l上运动.
根据模型提出问题:如果要使得PA+PB的值最小,那么,动点点P应该处在直线l的哪一处?
解析 作出所需的辅助线,作点A关于直线l的对称点,设为点A1,然后连接线段A1B,并且线段A1B与直线l相交产生交点,此交点为了符合题意时点P的位置,那么,PA+PB=A1P+PB=A1B.
方法解读 因为在作辅助线时,首先找的是点A关于直线l的对称点,点P在直线l上运动,所以不管点P在直线l上的哪一点,根据轴对称的特性可以知道:PA=A1P,这时这个题目就被转化为求A1P+PB的最小值,又因为求的是三个点之间的所连线段的最小值,因此,可以根据原理:“两点之间线段最短”,将三点化为两点,即当点A1、P、B共线时,A1P+PB可以取得最小值,从而实现了线段的“化”“折”“为”“直”.
二、问题探究
类型 几何图形中的线段与最值
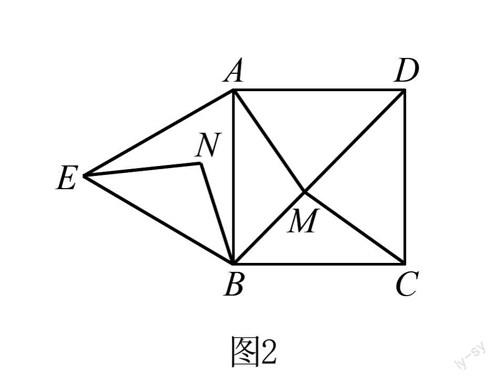
例1 如图2所示,此图由一个正方形ABCD和一个等边三角形ABE所组成,并且已知在正方形ABCD的对角线BD上有一个动点M,点M不与点B重合,如若将线段BM以点B 为旋转中心,逆时针旋转60°,这时点B落在了点N处,最后将CM、AM和EN连接起来,请根据以上条件回答问题.
(1)试证明:ΔAMBΔENB.
(2)①如要使得AM+CM有最小值,那么,点M应该在线段BD的哪一处;
②如果要使得AM+BM+CM有最小值,那么,这时点M又该位于和位置呢,请说明理由.
解析 对于第一小问,本小题比较简单,只需要根据正方形和等边三角形的性质,找到两个需要证明全等的三角形对应边相等即可,过程略.
第二小问,①这道题目和例题“将军饮马”很相似,解题方法是一样的,其中涉及三个点,由于两点之间线段最短,可以得出线段AC与线段BD的交点为点M时,就是题目所求的最小值的情况,那么,此时点M为BD的中点.
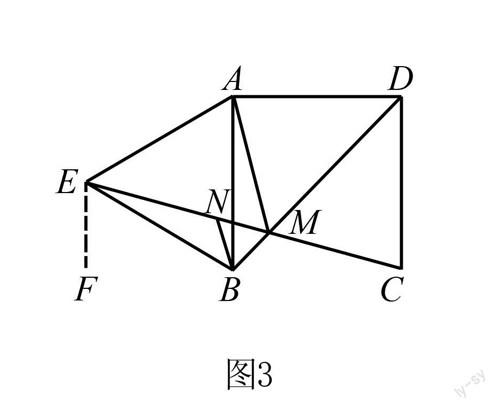
②求解线段和的最小值,我们需要采用等线段转化的方法,如图3所示,首先作出所需辅助线,连接CE、MN,然后过点E作CB延长线上的垂线,设垂足为点F,在这里我们需要利用第一小问的结论即△AMB△ENB,∴AM=EN,∠MBN=60°,MB=NB,∴△BMN為等边三角形,∴BM=MN,那么,AM+BM+CM=EN+MN+CM.
又两点之间线段最短,可知当点E、N、M、C共线时,有EN+MN+CM=EC,
综上所述,当点M为EC和BD的交点时距离最短.
解析 这道例题是几何图形的线段和最值问题,涉及三线、四点,但是不管怎样,解题的原理还是一样的,碰到需要化“折”为“直”的问题时,可以采用轴对称来进行变换,还可以利用“两点之间线段最短”的原理来确定最值的情况.
三、几何图形的周长最值问题
例2 如图4所示,在四边形ABCD之中有两个直角,分别为∠B和∠D,并且∠C=50°,已知点E位于线段BC上,点F位于线段DC上,试求当△AEF的周长取得最小值时,∠EAF的度数是多少?
解析 本道例题求解周长的最值问题,我们可以先确定ΔAEF周长最小时的情况,再来求∠EAF的度数,L△AEF=AE+AF+EF,需要根据基本的模型来进行转化才可以解出题目.
如图5,过点A作出关于BC的对称点M,再过点A作关于CD对称的点N,然后将MN连接起来,设线段MN与线段BC的交点为E,线段MN与线段CD的交点为F,那么在这时点M、E、F、N四点共线,AE+AF+EF=EM+NF+EF=MN,ΔAEF的周长是最小的.
由轴对称的特性可以知道,∠M=∠BAE,∠N=∠DAF,
又∵∠BAD=130°,并且∠M+∠N=50°,
∴∠BAE+∠DAF=50°,
∴∠EAF=130°-50°=80°.
本题属于几何图形周长的最值问题,需要结合周长公式将求解几何图形的最值问题转化为求解线段和的最值问题,此类题型的特点就在于它涉及到的线段和关键点更多,虽然难度增加了,但是只要掌握了原理,在实际分析时进行多次轴对称变换,这类题目就会迎刃而解.
通过上述几道例题的解析与思路分析,我们不难发现这类题型的关键点在于掌握“两点之间线段最短”原理,并根据原理进行多次转换就可以简化题目,根据轴对称的特性,做到化“折”为“直”,再结合“两点之间线段最短”找出动点满足题意的位置,当涉及三线、四点时,更应该找到线段相等的线段,将其替换,然后找到它们的交点,一般这个交点就是我们所求的点.不难发现,这类题型涉及的知识点还是挺多的,比如“两点之间线段最短”“垂线段最短”以及“线段平移”,还有轴对称的特性,因此,在平时就要求学生对这些基础知识点非常熟悉,并且需要掌握一些基础的问题模型,研究透这些模型,夯实基础,勤加练习才是最重要的.
参考文献:
[1]汪仁林,朱养锋.例析与圆有关的最值问题[J].中学生数学,2014(03):4-5.
[2]杨路.这类几何最值问题有意思[J].数理天地(初中版),2021(05):22-23.
[3]杨路.例谈几何最值问题的破解思考[J].数理化学习(初中版),2020(10):16-18.
[责任编辑:李 璟]

