立体几何复习应关注的题型

福建 廖旺华 童其林

立体几何是培养直观想象、逻辑推理、数学运算等数学核心素养的重要载体，是高中数学的重要内容，也是高考数学的重要组成部分——一般有2道或3道小题，1道大题，占22分左右.在立体几何的复习过程中，应不留死角，即应该全面复习，弄明白原理、公理、定理、推论、性质及其应用，也要关注一些重要题型，并不断提高空间想象能力、推理论证能力、运算求解能力、数学建模能力、创新能力等关键能力.以下题型值得我们关注.

一、教材的改编题

教材是知识的重要来源，高考试题来源于教材、改编于教材又往往高于教材，学好课本知识，做好课本习题是学习数学的重要方面.

例1如图所示，在正方体ABCD-A1B1C1D1中，M，E分别为棱BC，BB1的中点，N为正方形B1BCC1的中心，l为平面A1MN与平面D1BE的交线，则直线l与正方体底面ABCD所成角的大小为

( )

A.30° B.45°

C.60° D.90°

解析:由正方体的性质与条件得MN⊥平面ABCD，BE⊥平面ABCD，MN⊂平面A1MN,BE⊂D1BE，所以平面A1MN⊥平面ABCD，平面D1BE⊥平面ABCD，所以l⊥平面ABCD，l与平面ABCD所成角的大小为90°，故选D.

点评:课本上有一个习题(必修2，人教版第73页习题2.3第5题):已知平面α,β,γ满足α⊥γ,β⊥γ,α∩β=l，求证:l⊥γ.用文字语言描述就是两个相交平面和第三个平面都垂直，则这两个相交平面的交线和第三个平面垂直，利用此结论可快速解答本题.再比如必修2第73页习题2.3第6题也是重要结论:如果共点的三条直线两两垂直，那么它们中每两条直线确定的平面也两两垂直.

一般来说，在解答小题时，由于小题不要解答过程，所以可直接利用课本习题的结论进行推理，当然，若是需要过程的解答题，运用课本习题的结论就需要给出证明.

二、作图题

高考评价体系确立了符合考试评价规律的三个方面的关键能力群:第一方面是以认识世界为核心的知识获取能力群(获取知识，如信息迁移题、情境题.不仅运用以前的知识，也包括获取即时知识，如下面的例3)；第二方面是以解决实际问题为核心的实践操作能力群(实践操作，如下面的例2)；第三方面是涵盖了各种关键思维能力的思维认知能力群(推理论证能力、运算求解能力、空间想象能力、数学建模能力、创新能力，如下面的例6).

例2如图，在正方体ABCD-A1B1C1D1中，P为棱AA1上的一点.试过点P在平面ADD1A1上作一条直线PQ，使PQ⊥C1P，写出作法，并说明理由.

解析:如图，连接D1P,在平面ADD1A1内过点P作PQ⊥D1P，则PQ为所作的直线.

理由如下:

因为几何体ABCD-A1B1C1D1是正方体，所以C1D1⊥平面ADD1A1.

又PQ⊂平面ADD1A1，所以C1D1⊥PQ，且PQ⊥D1P，C1D1∩D1P=D1，

所以PQ⊥平面C1D1P，C1P⊂平面C1D1P，所以PQ⊥C1P.

点评:作图题其实就是实践操作能力题，在课本中能找到一些，如必修2(人教版)第59页例3，第63页B组第1题，第78页A组第2题等等.此类问题一般应添加辅助线，转化为线面、面面平行或垂直的问题.

不少立体几何问题——如小题，包括解析几何题，是不给出图形的，需要自己作图.作图能力是一项基本能力.

三、信息迁移题

所谓信息迁移题，是指在已有知识的基础上，设计一个陌生的数学情境，或定义一个新概念，或规定一种新运算，或给出一个新规划、新性质，通过阅读相关信息，根据题目引入新内容进行解答的一类新题型.由于信息迁移题背景新颖，构思巧妙，而且融综合性、应用性、开放性、创新性于一体，因此保证了考试的公平性，有利于考查学生的思维品质，有利于选拔有学习潜能的人才.同时它作为考试试题能有效地考查学生的阅读理解能力、探索能力、创新能力、抽象思维能力和综合运用数学知识的能力，有利于在数学教学中深化素质教育.因此，这类问题备受命题者的青睐.

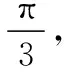
(Ⅰ)求四棱锥的总曲率；

(Ⅱ)若多面体满足:顶点数-棱数+面数=2，证明:这类多面体的总曲率是常数.

解析:因为四棱锥有5个顶点，5个面，其中四个侧面是三角形，一个底面是四边形，所以四棱锥的总曲率为5×2π-4π-2π=4π.

则多面体的总曲率为2πV-2π(E-F)=4π.

八省市联考数学卷向大家传递了这样一个信号:命题人办法是很多的.在对高考制度不进行大变的前提下，加强对于学生能力的考查，是完全可以做到的.建议多思考，多总结，切忌盲目做题(其中定义型的信息迁移题，就是对付盲目刷题的举措，值得关注)；花点时间读读教科书，包括初中和高中的教科书.

再强调一下，定义型的信息迁移题，其本质都是在考生原有认知水平的基础上，通过即时学习理解和掌握的新知识，考查考生在数学概念迁移到不同情景下的探究能力，从而检测考生进一步学习的潜能.解答这类问题，一是要读懂题意,通过转化,化“新”为“旧”；二是通过深入分析，多方联想，以“旧”攻“新”；三是创造性地运用数学思想方法，以“新”制“新”.

四、开放性问题

在“四翼”(基础性、综合性、应用性、创新性)考查要求下，新高考数学将有以下五种新题型:一是多选题，选择题答案不唯一，存在多个正确选项；二是逻辑思维题，以日常生活情境考查推理、论证、比较、评价等逻辑思维能力；三是数据分析题，给出一些材料背景以及相关数据，要求考生读懂材料，获取信息，根据材料给出的情境、原理以及猜测等，自主分析数据，得出结论，并解决问题；四是举例题，要求考生通过给出的已知结论、性质和定理等条件，从题干中获取信息，整理信息，写出符合题干的结论或具体实例；五是开放题，问答题设问开放，答案并不唯一，或者条件开放，或者条件和结论都开放，要求考生能综合运用所学知识，进行探究，分析问题并最终解决问题.

例4一副三角板由一块有一个内角为60°的直角三角形和一块等腰直角三角形组成，如图所示，∠B=∠F=90°，∠A=60°，∠D=45°，BC=DE，现将两块三角形板拼接在一起，得三棱锥F-CAB，取BC中点O与AC中点M，则下列判断中正确的是________.(填正确判断的序号)

①直线BC⊥平面OFM；②AC与平面OFM所成的角为定值；③设平面ABF∩平面MOF=l，则l∥AB；④三棱锥F-COM的体积为定值.

解析:由OM为△ABC的中位线得OM∥AB，则BC⊥OM,BC⊥OF，且OM∩OF=O，则BC⊥平面OFM，故①正确；

由BC⊥平面OFM，得AC与平面OFM所成角为∠CMO，而∠CMO=∠CAB=60°，故②正确；

如图，过点F在平面OMF内作直线l∥OM，而OM∥AB，所以l∥AB，l为平面OMF和平面ABF的交线，故③正确；

在三棱锥F-COM中，CO⊥平面OMF.由于CO为定值，△OMF的面积不为定值，所以三棱锥F-COM的体积不为定值，故④错误，

故选①②③.

点评:解决本问题的关键在于利用中点的性质，可利用中位线得平行，也可利用三线合一得垂直，解决线面垂直，线线平行，棱锥体积.

开放性问题包括条件开放型、结论开放型及条件和结论都开放型.本题是结论开放型问题，这类题目的特点是给出一定的条件，要求从条件出发去探索结论，而结论往往是不唯一的，甚至是不确定的，或给出特例后通过归纳得出一般性结论.解决此类问题的策略有从已知条件出发，运用所学过的知识进行推理、探究或实验得出结论；通过归纳得出一般性结论，再去证明；对多种结论进行优化(内含分类讨论)等.

例5如图，在直四棱柱A1B1C1D1—ABCD中，当底面四边形ABCD满足条件________时，有A1C⊥B1D1.(注:填上你认为正确的条件即可，不必考虑所有可能的情况)

解析:本题是条件探索型试题，即寻找结论A1C⊥B1D1成立的充分条件，由AA1⊥平面A1B1C1D1以及A1C⊥B1D1(平面A1ACC1的一条斜线A1C与平面内的一条直线B1D1互相垂直)，容易联想到三垂线定理及其逆定理.因此，欲使A1C⊥B1D1，只需B1D1与CA1在平面A1B1C1D1上的射影垂直即可.显然，CA1在平面A1B1C1D1上的射影为A1C1，故当B1D1⊥A1C1时，有A1C⊥B1D1.又由于直四棱柱的上、下底面互相平行，从而B1D1∥BD，A1C1∥AC.因此，当BD⊥AC时，有A1C⊥B1D1.由于本题是要探求使A1C⊥B1D1成立的充分条件，故当四边形ABCD为菱形或正方形时，得BD⊥AC，从而得A1C⊥B1D1，故可以填①AC⊥BD或②四边形ABCD为菱形，或③四边形ABCD为正方形中的任一个条件即可.

点评:AC⊥BD是结论A1C⊥B1D1成立的充要条件，而所填的ABCD是正方形或菱形则是使结论A1C⊥B1D1成立的充分而不必要的条件.本例题中，满足题意的充分条件不唯一，具有开放性特点，这类试题重在考查基础知识的灵活运用以及归纳探索能力.

条件开放型的特点是给出了题目的结论，但没有给出满足结论的条件，并且这类条件常常是不唯一的，需要解题者从结论出发，通过逆向思维去判断能够追溯出产生结论的条件，并通过推理予以确认.这种条件探究性问题实质上是寻找使命题为真的充分条件(未必是充要条件).解决此类问题的策略有两种，一种是将结论作为已知条件，逐步探索，找出结论成立所需的条件，这也是我们通常所说的“分析法”；第二种是假设题目中指定的探索条件，把它作为已知，并结合其他题设进行推导，如果能正确推导出结论，则此探索条件就可以作为题设条件，直觉联想、较好的洞察力都将有助于这一类问题的解答.

例6α，β是两个不同的平面，m，n是平面α及β之外的两条不同直线.给出四个论断:①m⊥n；②α⊥β；③n⊥β；④m⊥α.以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题:________.

解析:本题通过改变条件与结论之间呈现的顺序与组合，使问题具备了探索性，将分析—猜想—证明的思维过程巧妙地融入了解题过程；同时也使问题具有了开放性，走出了数学答案唯一确定的误区.以新颖的知识呈现方式改变学生的常规思维，考查学生的创新能力.

答案是:②③④⟹①或①③④⟹②.

点评:本题是条件和结论都开放型，即题目条件和结论都是不确定的，但是给出了一定量的信息和情景，要求解题者在题目给出的情景中，自行设定条件，自己寻找结论，自己构建命题并进行演绎推理.

五、考查空间想象能力和逻辑推理能力的问题

立体几何是培养逻辑推理和空间想象能力的重要载体.推理的依据就是立体几何的公理、定理、推理、性质等.

例7如图，AB是圆锥SO底面圆O的直径，D是圆O上异于A，B的任意一点，以AO为直径的圆与AD的另一个交点为C，P为SD的中点.现给出以下命题:

①△SAC为直角三角形；

②平面SAD⊥平面SBD；

③平面PAB必与圆锥SO的某条母线平行.

其中正确命题的个数是

( )

A.0 B.1

C.2 D.3

解析:①如图，连接CO，因为AO是小圆直径，所以AC⊥OC.因为OA=OD，所以C为AD的中点，因为SA=SD，所以SC⊥AD，所以△SAC为直角三角形，所以①正确；

②作BE⊥SD于点E，若平面SAD⊥平面SBD，则BE⊥平面SAD，所以BE⊥AD，因为AB是圆锥SO底面圆O的直径，所以BD⊥AD，BE∩BD=B,所以AD⊥平面SBD，所以AD⊥SD，由①可知SC⊥AD，所以SC∥SD，与SC∩SD=S相矛盾，故②错误；

③如图，延长DO交大圆O于点H，连接SH，OP，则有SH∥OP.因为SH⊄平面PAB，OP⊂平面PAB，所以SH∥平面PAB，故③正确，

故选C.

点评:正确的命题需要证明，错误的命题只需要举出一个反例——通过反例，判断命题错误也是一种重要的能力.

例8如图，三棱柱ABC-A1B1C1中，底面ABC是等边三角形，侧面BCC1B1是矩形，AB=A1B，N是B1C的中点，M是棱AA1上的一点，且AA1⊥CM.

(Ⅰ)证明:MN∥平面ABC；

(Ⅱ)若AB⊥A1B，求二面角A-CM-N的余弦值.

解析:(Ⅰ)证法一:如图，在三棱柱ABC-A1B1C1中，连接BM，因为BCC1B1是矩形，所以BC⊥BB1.

因为AA1∥BB1，所以AA1⊥BC.

又因为AA1⊥MC，BC∩MC=C，所以AA1⊥平面BCM，

所以AA1⊥MB.又因为AB=A1B，所以M是AA1的中点.

所以NP∥MA且NP=MA，所以四边形AMNP是平行四边形，所以MN∥AP.

又因为MN⊄平面ABC，AP⊂平面ABC，所以MN∥平面ABC.

证法二:如图，在三棱柱ABC-A1B1C1中，连接BM.因为BCC1B1是矩形，

所以BC⊥BB1.因为AA1∥BB1，所以AA1⊥BC.

又因为AA1⊥MC，BC∩MC=C，所以AA1⊥平面BCM，所以AA1⊥BM.又因为AB=A1B，所以M是AA1中点.

取BB1的中点Q，连接NQ，MQ.因为N是B1C的中点，所以NQ∥BC.

因为NQ⊄平面ABC，BC⊂平面ABC，所以NQ∥平面ABC.

因为M是AA1的中点，所以MQ∥AB.

因为MQ⊄平面ABC，AB⊂平面ABC，所以MQ∥平面ABC.

因为MQ∩NQ=Q，所以平面MNQ∥平面ABC.

因为MN⊂平面MNQ，所以MN∥平面ABC.

在△BCM中，CM2+BM2=2a2=BC2，所以MC⊥BM.

解法二:如图，因为AB⊥A1B，所以△ABA1是等腰直角三角形.

在△BCM中，MC2+BM2=2a2=BC2，所以MC⊥BM.

又因为MC⊥AA1，AA1∩BM=M，AA1⊂平面ABB1A1，BM⊂平面ABB1A1，

所以MC⊥平面ABB1A1.

连接MB1，因为MB1⊂平面ABB1A1，所以MC⊥MB1，

点评:问题(Ⅰ)只要能正确分析线面垂直的位置关系，证得M是中点，再根据直线与平面平行的判定定理或平面与平面平行的性质即可得证.问题(Ⅱ)只要能正确分析数量关系并通过勾股定理得出MC⊥MB，从而得到MA1，MB，MC两两垂直，建立空间直角坐标系，求出各点坐标，得到平面MNC的法向量，从而求解.或者能正确分析数量关系并通过勾股定理得出MC⊥MB从而得到MC⊥平面AA1B1B，进而得到MC⊥MB1.再根据MC⊥MA，从而得到∠AMB1就是二面角A-CM-N的平面角，再在Rt△BMB1中分析数量关系求得∠BMB1的正弦值，再利用诱导公式得到∠AMB1的余弦值.