超混沌系统的控制研究
周群利
(芜湖职业技术学院电气与自动化学院,安徽芜湖 241006 )
0 引言
混沌运动是一种广泛存在于数学、物理、生物、化学、地质以及某些技术性科学中的动力学行为,它具有对初始条件极度敏感、遍历性以及类似于随机系统的伪随机性等性质.混沌现象由某些确定性的系统产生,并由耗散和非线性两种运动共同作用而形成的结果.它在耗散型的作用下在宏观上表现为相体积的收缩和稳定的现象,而在非线性运动的作用下导致了混沌系统轨道的不稳定性,从而使得运动轨道逐渐地局部分离,混沌运动和混沌现象就是在宏观的稳定与微观的不稳定的共同作用下产生的[1].相比于低维的混沌系统,超混沌系统(维数大于 3)具有更多正 Lyapunov 指数,具有更为复杂的动力学行为[2],从而使得超混沌系统的动态特性更加复杂、混沌程度更高.超混沌系统被广泛用于各个领域且具有非常广阔的应用前景[3-4].此外,超混沌系统的混沌吸引子也不具有几何直观性,所以相比于现有的低维混沌系统形状同步的研究成果,高维混沌系统控制的研究具有更高的难度[5].在一些实际应用中,混沌系统显得较为简单,已不能满足人们的需要,因此对超混沌系统的深入研究对于理论和实际运用都具有重大意义[6].
混沌控制在工程技术上有着重大的研究价值和广阔的应用前景,引起了国际上非线性动力系统和工程控制专家的极大关注[7-10].自混沌与超混沌的概念被提出以来,学者们一直致力于对混沌与超混沌系统的研究,并将其应用于保密通信、信息安全与工业等领域[11].
Liu等在2004年提出了一种三维自治混沌系统[12],文献[13]在已有的三维Liu 系统基础上通过增加一个新的状态变量和微分方程来构造一个全新的超混沌系统.本文对此超混沌系统进行动力学分析,采用自适应控制方法通过设计合适的控制器对系统进行控制,并用Matlab(R2014a)数值仿真证明该方法的有效性,为这一类超混沌系统的控制问题提供一种行之有效的控制思路.
1 一个新的超混沌系统的数学模型
文献[13]在Liu系统的模型基础上,提出了一种新的超混沌系统的数学模型,系统由十项构成,含有四个非线性项,其形式如下:

(1)
当系统参数取值为:a=19,b=8,c=42,d=2时,系统处于超混沌状态,文献[13 ]分析计算了它的混沌特性参数,在此不再赘述.由Matlab(R2014a)软件编程计算结果可知,系统有3个平衡点,分别为:Q1(0,0,0,0),Q2(38.08,8.823,42,185.292),Q3(-38.08,-8.823,42,-185.292),利用此软件可求出系统在这些平衡点处的特征值.经Matlab软件编程求解发现:每个平衡点处所对应的特征值均存在正实部的特征根,所以系统的3个平衡点均不是稳定的平衡点,属于不稳定的鞍点.
当在该组参数下系统初值取[x,y,z,w]T=[0.01,0.01,0.01,0.01]T时,系统的混沌吸引子如图1所示,从图1可以看出,该超混沌系统蕴含着非常丰富的动力学特性,系统状态变量变化毫无规律可循,其相轨迹在混沌吸引子内盘绕折叠,呈现出总体吸引,但局部排斥且有界的精细的结构,这种结构是典型的混沌系统所具有的,在初始参数取值下,系统最终进入非周期的混沌运动.

图1 一个新的超混沌系统的混沌吸引子Fig.1 Chaotic attractor of a new hyperchaotic system
2 一个新的超混沌系统的自适应控制
控制系统最重要的特性是它的稳定性,一个不稳定的控制系统不但无法完成预期的控制任务,而且还存在一定的潜在危险性.稳定性指的是,如果一个系统在靠近其期望工作点的某处开始运动,且总是能保持在期望工作点附近运动,那么就称该系统是稳定的.在许多工程应用中,仅有李雅普诺夫意义下的稳定是不够的.一些工程要求由渐近稳定性概念来表达.对于一个自治系统,如果平衡点xe=0是稳定的,而且存在δ>0,使得当


受控的新的自治超混沌系统为:
(2)
其中U=[u1,u2,u3,u4]T为要设计的控制器,在系统参数未知的情况下,采用自适应控制方法,对系统(1)式设计控制律和参数自适应律,使新的超混沌系统状态稳定到系统的任意一个不稳定的平衡点Q(x0,y0,z0,w0).在系统的任意一个不稳定平衡点Q(x0,y0,z0,w0)处,对新的超混沌系统的数学模型(1)式进行坐标变换,状态变量设为
(3)
将(3)式代入受控的新的超混沌系统(2)式得:
(4)
从而将超混沌系统(1)式控制到任意一个不稳定平衡点Q(x0,y0,z0,w0)的问题转化为变换后的系统(4)式在坐标原点的镇定问题.
定理对于变换后的系统(4)式设计如下的控制器:
(5)
以及参数自适应律
(6)
时,变换后的受控系统(4)式在原点是渐近稳定的.即受控的新的超混沌系统(2)式被控制到不稳定平衡点Q(x0,y0,z0,w0).(5)、(6)两式中a1,b1,c1,d1分别为对未知参数a,b,c,d的估计值,控制增益k1,k2,k3,k4均大于零.
证明:(5)、(6)两式代入(4)式得:
(7)

对V求导并化简可得:

3 系统仿真结果
采用自适应控制方法对一个新的超混沌系统进行控制,使其镇定到系统的任意一个不稳定平衡点,假定这个平衡点取为Q2(38.08,8.823,42,185.292),假设“已知”系统参数为(a,b,c,d)=(5,5,4,8),系统初始状态取值((x(0),y(0),z(0),w(0))=(0.01,0.01,0.01,0.01),系统参数估计值初始值取为((a1(0),b1(0),c1(0),d1(0))=(7,4,-5,-2),系统控制增益取值为(k1,k2,k3,k4)=(6,8,7,10).
下面利用Matlab软件进行系统仿真.从图2可以看出超混沌系统(1)式在所设计的控制器及自适应律作用下四个状态变量在1.5s左右稳定控制在系统的其中一个不稳定平衡点Q2(38.08,8.823,42,185.292),图3为参数a1,b1,c1,d1对未知参数a,b,c,d的估计收敛曲线,在2s左右的时间里参数a1,b1,c1,d1即可稳定收敛于其相应的估计值.当适当增加系统控制增益时,超混沌系统(1)式四个状态变量被稳定控制在其中一个不稳定平衡点Q2(38.08,8.823,42,185.292)的速度加快,同时系统参数a1,b1,c1,d1稳定收敛于其相应的估计值的速度也加快了,从而提高了系统的响应速度,满足了控制要求.当取系统控制增益(k1,k2,k3,k4)=(20,13,12,15)时仿真结果如图4、图5所示,从仿真结果可以看出四个状态变量在1s内即可稳定收敛于不稳定平衡点Q2(38.08,8.823,42,185.292),系统参数a1,b1,c1,d1稳定收敛于其相应的估计值大约只需要1s左右.
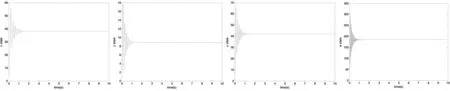
图2 超混沌系统(1)式的状态被控制到不稳定平衡点Q2Fig.2 The state of hyperchaotic system (1) is controlled to the unstable equilibrium point Q2

图3 a1,b1,c1,d1对系统未知参数a,b,c,d的估计收敛曲线Fig.3 Convergence curve of estimation a1,b1,c1,d1 for unknown parameters a,b,c,d of system

图4 超混沌系统(1)式的状态被控制到不稳定平衡点 Q2(仿真)Fig.4 The state of hyperchaotic system (1) is controlled to the unstable equilibrium point Q2(Simulation)

图5 a1,b1,c1,d1对系统未知参数a,b,c,d的估计收敛曲线(仿真)Fig.5 Convergence curve of estimation a1,b1,c1,d1 for unknown parameters a,b,c,d of system(Simulation)
以上仿真结果表明自适应控制方法对超混沌系统(1)式的控制是完全有效的.也可以设计合适的控制器和参数自适应律,将超混沌系统的状态控制到其他的不稳定平衡点,在此不再赘述.
4 结论
对一个新的超混沌系统采用自适应方法进行控制,设计了合适的控制器以及参数自适应律,在其作用下可将超混沌系统的状态快速地控制到系统的任意一个不稳定平衡点,同时还可对超混沌系统的未知参数进行估计,在极短时间内可使未知参数的估计值收敛于一个恒定值.仿真结果表明自适应控制方法是处理参数不确定混沌系统的有效方法,为其它非线性不稳定系统的控制提供了一种行之有效的解决思路.

