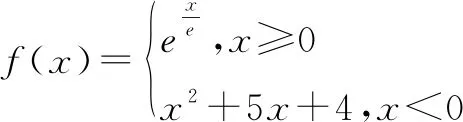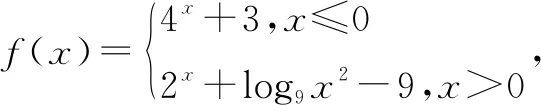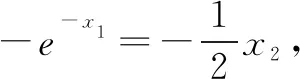抽丝剥茧探本源 步步为营巧推断
——基于函数的复合方程求解
李秀元 武 刚
(1.湖北省武穴市实验高级中学 435400;2.湖北省武穴中学 435400)
函数零点是高中数学一个重要概念.考查函数的零点,对于等价转化和数形结合思想方法培养有着非常重要意义.函数的零点,即函数图像与x轴交点的横坐标,也即对应方程的根.因此,基于函数的复合方程根的问题,最终将回归到基本函数的零点,研究基本函数的图像,从形上实现问题的求解.
一、解方程确定函数的零点
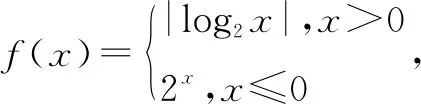
A.5 B.4 C.3 D.6

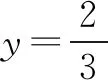

图1
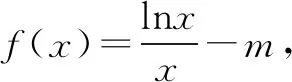
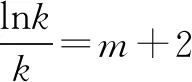
方程[f(k)]2-f(k)-2=0有两个不同的实数解,等价于:
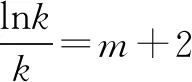
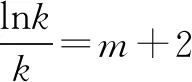
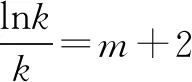
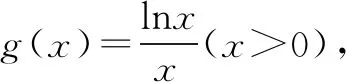


图2
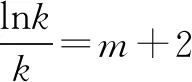


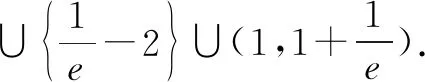
评析无论是求复合函数零点个数,还是依据复合方程根的个数求参数取值范围,都是基于函数的零点与方程根的关系,通过解方程,将复合函数的零点问题,转化为基本函数方程根的问题,借助于基本函数的图像,确定问题的解.此类问题主要考查解方程及研究函数图像,突出数形结合思想方法的运用.
二、简化方程,研究基本函数图像以确定参数取值范围
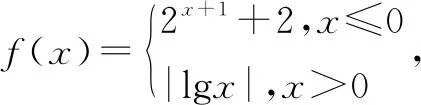
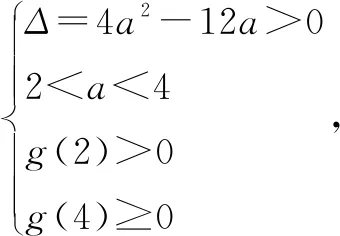
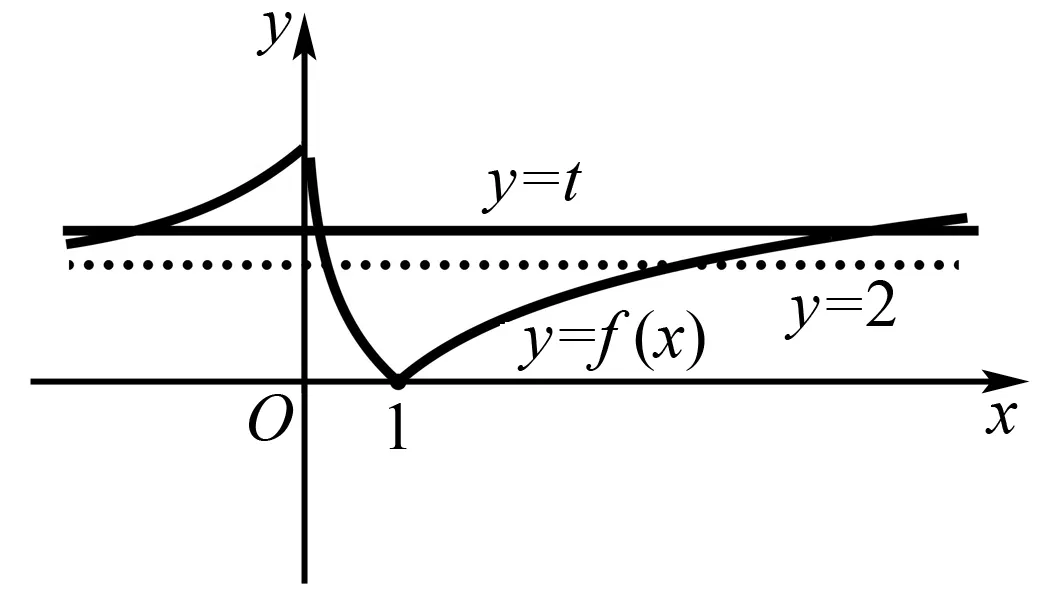
图3
例4 已知函数f(x)=(ex-1)2-|ex-1|+k,给出下列四个命题:
①对∀k∈R,函数不可能有4个零点;
②∃k∈R,函数有且只有1个零点;
③当且仅当k=0时,函数恰有2个零点;
④∃k∈R,函数有3个零点.
其中正确命题的个数是( ).
A. 4 B. 3 C. 2 D. 1

图4
评析即使复合函数(方程)类似,但因无法直接求出方程的根.对f(x)换元后,构造出两个方程(函数),结合基本函数的图像特点,通过研究基本方程解的存在情况,确定复合方程解的存在性,从而确定问题的解.数形结合依然是求解的利器,但逻辑推理亦不可或缺.
三、利用函数性质,解套对应法则
例5 已知奇函数f(x)是定义在R上的单调函数,若函数g(x)=f(x2)+f(a-2|x|)恰有4个零点,则实数a的取值范围是____.
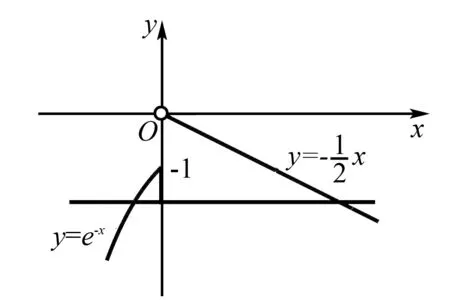
解因为f(x)为奇函数,令g(x)=0,则f(x2)=-f(a-2|x|)=f(2|x|-a).又f(x)为R上的单调函数,所以x2=2|x|-a.从而方程x2=2|x|-a有4个实根,即y=a与y=-x2+2|x|的图像有4个交点.作函数y=-x2+2|x|的图像如图5.因此,0 图5 评析由于没有明确的函数解析式,基于抽象函数的复合函数零点问题,利用抽象函数的奇偶性,将方程转化为两个独立的函数值相等的形式,再利用函数的单调性,解套对应法则,得到基本方程类型,再根据数形结合得到问题的解. A. 2 B. 3 C. 4 D. 5 解函数h(x)的零点,即方程f(f(x))=f(x)的根.令f(x)=t,则有f(t)=t.先求方程f(t)=t的根,对应于函数y=f(x)与y=x的图像交点横坐标.由于y=x与y=f(x)相切于点(-2,-2)和(e,e),故f(t)=t的根为t=-2和t=e,如图所示. 图6 由f(x)=-2可知方程有2解;由f(x)=e可知方程有3解. 因此,函数h(x)=f(f(x))-f(x)有5个零点. A.2 B.4-4ln2 C.4+2ln2 D.1-3ln2 图7 原方程的根由f(x)=t确定,要使原方程恰有两个不等实根,根据f(x)的图像可知,t≤-1且t唯一. 令y=4x+2e-x(x≤0),则y′=4-2e-x. 由y′>0,得-ln2 所以,函数y=4x+2e-x是(-∞,-ln2)内的减函数,(-ln2,0)内的增函数,从而4x1+x2的最小值在x=-ln2时取得,值为-4ln2+2eln2=4-4ln2,选B. 评析对于嵌套函数(方程),将f(x)换元后,原方程转化为方程组,但最终复合函数的零点是由f(x)=t来确定,而t的个数和范围直接决定方程f(x)=t解的个数.显然,函数y=f(x)的图像,在试题求解中依然起着举足轻重的作用.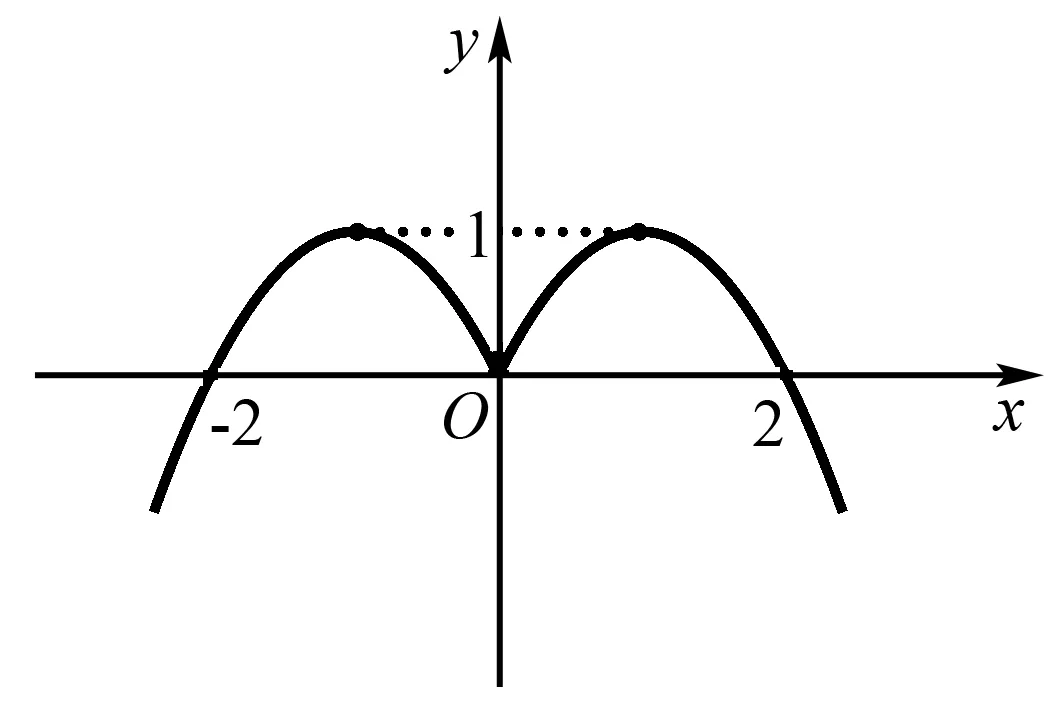
四、换元解嵌套函数方程