寻找临界点 巧破恒成立

刘明远

(河北省滦南县第一中学 063500)

“不等式恒成立求参数的取值范围问题”一直活跃在各级考试之中，尤其是高考题中尤为常见．因为这类题目综合性强，难度大，能力要求高，很多学生望而生畏，无从下手，但这种题目中，其本质根源在于参数变化时，函数的图像与x轴的关系出现交、切这两种临界情况，所以寻找临界值点——区间端点和切点，此类问题便可轻松求解，下面举例说明．

一、只存在“切点”

若函数在所给区间的端点没有意义，则只考虑切点，便可求出参数的取值范围．

例1(2020年高考山东卷·21)已知函数f(x)=aex-1-lnx+lna．

(1)当a=e时，求曲线y=f(x)在点(1，f(1))处的切线与两坐标轴围成的三角形的面积；

(2)若f(x)≥1，求a的取值范围．

分析(1)略．(2)因为定义域为(0，+∞)，所以此类题目的临界值没有“区间端点”，因此只考虑“切点”，便可求出参数的取值范围，即f(x) 与y=1相切．

综上，该题结果为a≥1．

解析(1)略．

(2)由f(1)≥1得a+lna≥1，解得a≥1．

当a≥1时，f(x)=aex-1-lnx+lna≥ex-1-lnx．

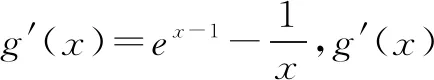
二、只存在“区间端点”

若函数在所给区间不能与x轴相切，则只考虑区间端点，当函数在区间端点有意义，应先代入端点值满足题设，若此时不能求出参数的范围，则考虑变量分离，用端点的极限值便能求出参数的范围．

例2(2010年新课标卷·21)设函数f(x)=ex-1-x-ax2．若当x≥0时f(x)≥0，求a的取值范围．

分析①考虑区间端点．f(0)=0显然成立，即a∈R，所以此时应考虑极限值．

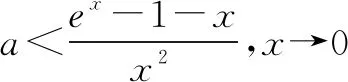
②考虑相切．设f(x)与x轴相切于(t，0)(t>0)，则f(t)=0；f′(t)=0，所以et-at2-t-1=0；et-2at-1=0，消去a得(t-2)et+t+2=0，解得t=0(舍)．

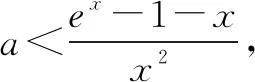
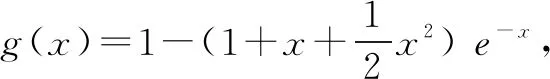
三、存在“区间端点”和“切点”

若函数在所给区间端点处有意义且存在与x轴相切的情况，则参数的范围为两种临界状态的交集．

例3(2013年高考全国Ⅰ卷·21题改编)已知f(x)=x2+4x+2，g(x)=ex(2x+2)，若x≥-2时，f(x)≤kg(x)，求k的取值范围．

分析①考虑区间端点．f(-2)≤kg(-2)，所以-2≤-2ke-2，因此k≤e2．

②考虑相切．设h(x)=f(x)-kg(x)与x轴相切于(t，0)，则h(t)=0；h′(t)=0，所以t2+4t+2-ket(2t+2)=0；2t+4-ket(2t+4)=0，解得t=0或-2，所以由f(0)≤kg(0)得2≤2k，解得k≥1．

综上，该题结果为1≤k≤e2．

解析由f(-2)≤kg(-2)得k≤e2；由f(0)≤kg(0)得k≥1，所以1≤k≤e2．

设函数F(x)=kg(x)-f(x)=2kex(x+1)-x2-4x-2，则F′(x)=2kex(x+2)-2x-4=2(x+2)(kex-1)．

令F′(x)=0，得x1=-lnk，x2=-2．

(2)若k=e2，则F′(x)=2e2(x+2)(ex-e-2)，从而当x>-2时，F′(x)>0，故F(x)在(-2，+∞)单调递增，而F(-2)=0，故当x≥-2时，F(x)≥0，即f(x)≤kg(x)恒成立．

综合，k的取值范围是[1，e2]．

例4(2020年高考全国Ⅰ卷理科·21)已知f(x)=ex+ax2-x．

(1)当a=1时，讨论f(x)的单调性；

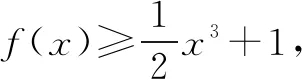
分析(1)略．

解析(1)略．

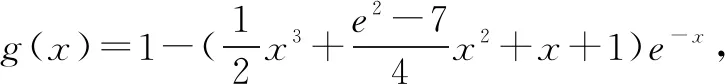
从以上4例可以看出，参数的取值范围主要与临界值点——区间端点和切点有关，从这两种点出发，求出各自对应的参数的取值范围，最终的交集就是题目答案，这种方法尤其对于选择填空题更为有效，读者可以自行实验，在此不再赘述．